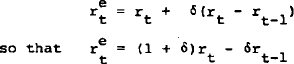RDP 7902: Financial Modelling in Australia 3. Full Model Studies
September 1979
The full model studies of financial interactions to be discussed are:
- RBA1 (Norton and Henderson (1971));
- RBA76 (Jonson, Moses and Wymer (1976)[9]);
- RBF (Kiernan (1977b));
- NIF (Johnston (1977), Johnston and Perrin (1978)[10]);
- Melbourne Institute (Derody and Sheehan (1977)).
3.1 Theory
3.1.1 Consistencies
All the models have a consistent theoretical structure although detail of coverage differs. With the exception of RBA76 all the models use a modified stock adjustment structure in which only own disequilibrium effects are specified. The separate agents in each of the models are: the government; the financial institutions; and the aggregate corporate and household sectors. RBA76 treats the financial institutions sector as all banks whilst RBA1 and Melbourne Institute disaggregate the banking sector into savings and trading banks. RBF considers savings and trading banks, as well as building societies, whilst N.I.F. models the behaviour of savings banks, trading banks, building societies and official money market corporations.
As is the case with the sectoral studies it is necessary to account for the relevant balance sheet constraints. It can be seen from table 2 that each of the studies contains a formation table identity.[11] Some component of money holdings is determined in the identity. The formation table does not impose an explicit balance sheet constraint on the household/corporate sector because some sources of income such as changes in the market value of financial assets are not taken into account. It does, however, ensure that one of the financial assets held by the corporate/household sector responds rapidly to absorb certain changes in disposable nominal income. Sources of these changes include variations in government expenditure and tax rates and movements in the balance of payments.
A test of whether money is an appropriate choice for such a role is provided in the results from the single sector portfolio studies. As discussed, the evidence here is not conclusive. One shows that liquid assets absorb the major part of the income change, whereas others give overwhelming importance to equities. If equities are important, then the full model studies which aggregate the corporate and household sectors and do not explicitly consider the equity market will be sacrificing important information.
Table 2 also shows the asset which is determined as the residual in the balance sheet identity of the banking system. In all cases the residual asset is the most liquid in the portfolio. Support for this choice is provided by Sharpe's estimates for the portfolio behaviour of the savings banks. As with the household/corporate sector however, the evidence is not clear cut. For instance Shaw, in his portfolio analysis of life assurance companies, found that liquid assets absorbed very little of the initial increase in total assets.[12]
3.1.2. Wealth
RBA1 is the only full model study that goes beyond the formation table to impose a wealth identity on the household-corporate sector. Wealth is defined as the market value of all domestic non-official claims on the government sector plus the market value of all physical capital and consumer durables owned by domestic residents. The market value of physical capital is calculated as that value which equates the rate of return on physical capital with the market interest rate adjusted for price expectations. This approach has the advantage over the formation table identity of allowing for changes in the market value of financial and physical assets to affect the private sector's balance sheet and subsequent portfolio allocation. In RBA1, total wealth affects investment in dwellings, household durables, and motor vehicles. This is a similar approach to that used in the later sectoral study by Clements (1976) where total spending-power affects expenditure and asset demand decisions. It is clear, however, that Norton and Henderson (1971) favoured the approach of disaggregating wealth which was subsequently used by Parkin et al and Purvis when alluding to experimenting with “some weighted average of the components of private sector wealth”. (p. 62)
| Study | Formations Table Residual | Banking Sector Balance Sheet Residual | Non-Bank Financial Institutions |
|---|---|---|---|
| Jonson, Moses and Wymer (1976) | M3 | Total bank holdings of government securities and currency | – |
| Derody and Sheahan (1977) | Trading bank fixed deposits plus savings bank deposits | Savings bank government securities Trading bank government securities |
– |
| Kiernan (1977) | Trading bank current deposits | Trading bank government securities Savings bank government securities |
Permanent building societies |
| Johnston (1977) and Johrston and Perrin (1978) | Trading bank current deposits | Trading bank government securities Savings bank deposits with the Reserve Bank |
Permanent building societies official short term money market corporations |
|
* As discussed, the formation table does not appear explicitly in RBA1. The banking sectors holdings of government securities are determined resicually in the government's financing idertity, and trading bank deposits are determined as the residual in the bank's balance sheet identity. |
|||
The presence of the wealth identity in RBA1 does not mean that the properties of the formation table approach are not apparent in the RBA1 treatment. In particular, the monetary effect of a change in official budgetary policy or in official holdings of international reserves has a similar instantaneous impact on the money supply as in the formation table approach. In RBA1, the effect works through the government financing identity and the aggregate balance sheet identity of the banks. An increase in the budget deficit or in foreign reserves is initially absorbed in holdings of government securities by the banking system. Through the banks' balance sheet identity the increase in the holdings of government securities by the banks leads to an instantaneous increase in bank deposits.
The importance of the use of wealth is that the influence of fluctuating asset values on economic behaviour can be captured. The links found by Norton and Henderson are not strong, although this could reflect the very stable interest rates which prevailed during the sample (1958(4) to 1969(4)).
3.1.3 Monetary Disequilibrium
The only model which estimates a more complete structure than the simple modified stock adjustment model is RBA76. In this model, the disequilibrium of the residual asset (M3) affects expenditure, holdings of other financial assets and prices. Relative to some of the sectoral studies, which use the separate disequilibria of all the other assets in the portfolio in equations for household expenditure and the holdings of other assets, this represents a simplification. However, the use of monetary disequilibrium (in addition to the own disequilibrium) considerably reduces the statistical problems found by the general sector studies. Perhaps, partly as a result of this simplification, significant statistical evidence is found for the feedback role of monetary disequilibrium.[13]
The theoretical analysis in the appendix suggests that the asset with the lowest costs of adjustment will have the smallest role of all assets in its disequilibrium feedback effects on expenditure and other asset holdings. Jonson (1978a), (1978b) accepts the position of the sectoral studies that the relevant disequilibrium effects may come from all assets although he suggests two possible reasons why the simpler approach of relying on monetary disequilibrium may be a good first approximation.
- “monetary disequilibrium is a good proxy for asset disequilibrium in general if the composition of portfolios adjusts relatively rapidly” (1978a, p. 17);
- “this argument for the uniqueness of money is based on the existence of information and transactions costs in an uncertain world” (1978b, p. 4).
Neither of these arguments seems to provide a wholly convincing, rationale for the specification of RBA76. First, the available evidence suggests that speeds of adjustment of the various assets are different, implying that the composition of portfolios does not adjust relatively rapidly (Tables 3–7). This evidence is not complete since the speeds of adjustment of various assets can only really be tested using simulation analysis of a generalised portfolio system. The evidence here has not yet been provided. It seems reasonable, however, that because of its volatile properties the residual asset, in particular, will adjust more slowly than other assets in the portfolio. Second, Helliwell (1977, p. 82) believes that the signalling role for monetary disequilibrium used in the second of the above arguments should be played down because “it is just as easy to think of the changes that gave rise to the change in money balances as providing the signal.”
Helliwell (1977, p. 83), however, argues strongly for the inclusion of the residual asset disequilibrium in the expenditure and asset holding equations since “it is crucial that the modelling be done so the cumulant of past buffering changes be fed back into some adjustment process so that the long-run stock of the asset in question is appropriately defined and suitable pressures are put on the actual stock to adjust it to that long-run desired level”. This effect is, of course, important for the consistent long-run properties of the model. However, it does not reasonably provide a case for residual asset disequilibrium feeding back in the expenditure and all other asset holdings equations nor does it necessarily justify residual asset disequilibrium appearing in place of the other disequilibrium effects in these equations.
A further justification of the use of the residual asset disequilibrium feedback effect is suggested by Jonson's (1978b, p.3) use of the Tobin-Brainard (1969) observation that “new saving is initially accumulated as demand deposits, later to be distributed among other assets if holdings of demand deposits are too large”. This suggests that residual asset disequilibrium may be a good proxy for an impact increase in the size of the portfolio.[14] It is important to note, however, that residual asset disequilibrium will not be a good proxy for the change in the value of the portfolio in discrete time models since the term ( ) will not capture the within period rise in the holdings of the residual asset. However, this will not be the case with models such as RBA76, which are specified in continuous time.
) will not capture the within period rise in the holdings of the residual asset. However, this will not be the case with models such as RBA76, which are specified in continuous time.
Different proxies for the short-run increase in the portfolio value of the non-bank groups are used in RBA1 and RBF for the financial asset equations, although no similar effect is evident in the expenditure equations in RBA1.[15] Both these studies use a measure of the increased indebtedness of the authorities. (RBA1 uses the gross domestic borrowing requirement, and RBF uses the liquidity base.) Whilst, with respect to short-run movements, the approach of RBA1 may give similar results to that of RBA76, in the longer-run the dynamics of adjustment will be different since RBA76 takes explicit account of the effect of changes in the long-run demand for the residual asset.
The other important role of monetary disequilibrium in RBA76 is its effect on prices. The two justifications for this effect, which is supported by the econometric evidence, are:
- price setters are faimilar with the effect which excess money has on expenditure and recognise that changing money is a useful signal that prices can be raised (Jonson (1978b));
- monetary disequilibrium can be identified with the gap between anticipated and actual money holdings in the tradition of rational expectations (Clements and Jonson (1979)).
If supported by further work, the direct effect of money on prices would represent an important step forward in our understanding of the dynamics of inflation and the links between the real and financial sectors. In this context it is worth noting that several single equation studies of the formation of inflationary expectations in Australia – by Jonson and Mahoney (1973), Valentine (1975), Taylor (1976) and Defris and Williams (1979) – provide evidence that the money supply plays some role. only the study by Taylor considered the role of monetary disequilibrium.
3.1.4 Interest Rates
i) Nominal or Real?
All the studies relate nominal financial asset holdings to nominal interest rates with the exception of RBF which relates real asset demands to nominal interest rates.
Real interest rates affect the demand for real household expenditure and business investment in RBA79.[16] Since the demand for money is a function of nominal interest rates, expenditure in RBA76/9 is influenced by these rates too. In RBA1, both real and nominal interest rates affect expenditure and investment. Real interest rates work through their impact on the market value of the capital stock which is a component of wealth. Another component of wealth is the market value of financial claims on the official sector. This is affected by nominal interest rates. Nominal interest rates also affect investment through their influence on the implicit rental price of capital. Interest rates do not play a major role in the expenditure and investment equations of the NIF model. The only direct effect is through the influence of the two year nominal government bond rate on real dwelling expenditure. In RBF, nominal interest rates directly affect real household expenditure and dwelling construction, whilst the implicit rental price of capital services, of which a nominal interest rate is a component, affects investment.
ii) Explanation
Although the full model studies have the scope to explain interest rates, little attention has been given to this so far. All rates of return on financial assets are exogenous in RBA1; this, in part, reflects the tight control which the authorities exercised over interest rates during the sample period although policy reaction functions were estimated for this period by Jonson (1974).
Some success has been attained in RBA76 and RBF in modelling the government bond rate in terms of a policy reaction function. In RBF, the authorities adjust the two year bond rate in response to the eurodollar rate and the non-bank take-up of government securities. In RBA76, the 10 year government bond rate adjusts to the rate of change of the money supply, the unemployment rate, the rate of change of foreign reserves and the ratio of foreign reserves to the money supply. Our inadequate understanding of the authorities reactions is reflected not only in the quite different specifications of these two equations but also in a comparison of the implied speeds of adjustment in the two sets of parameter estimates. In RBF the speed of adjustment of the authorities is approximately 20 times faster than that estimated in RBA76.
RBF and later versions of RBA76 (see Evans (1979)) also explain a short term market interest rate. In RBF, the rate on trading bank certificates of deposit is modelled as an equilibrium supply response of the trading banks. It is related to the maximum rate on large trading bank fixed deposits and the proportion of their free deposits not held in advances. In RBA76, a security of similar maturity, the 90 day commercial bill rate, is modelled as an equilibrium response to the eurodollar rate adjusted for exchange rate expectations and the ratio of trading bank excess liquid assets to bank advances.
Both equations have significant coefficients of the expected sign and are broadly similar in specification. There is little evidence about their simulation performance.
(iii) Expectations
Statistical studies of the market for Australian government securities (see e.g. Juttner et al (1975)) have shown the market to be inefficient. Consequently, information is available to the market participants that is not contained in the current market yields. Various attempts to model how this information is used to explain the take-up of government securities have been made in the Australian model studies.
In an early study which was part of the RBAI model project, Jonson (1972) built on earlier work on the non-bank take-up of government securities by Deane (1970) by including a term  as an explanatory variable in the equation. He found that this term – a proxy for capital gains or losses on holdings of government securities – produced considerable improvement to the sample fit for the period from 1962(2) onwards. The term was estimated with a significant positive coefficient, suggesting that these groups reduce their bond holdings before an anticipated rise in the interest rate.
as an explanatory variable in the equation. He found that this term – a proxy for capital gains or losses on holdings of government securities – produced considerable improvement to the sample fit for the period from 1962(2) onwards. The term was estimated with a significant positive coefficient, suggesting that these groups reduce their bond holdings before an anticipated rise in the interest rate.
Shaw (1973) used the future quarterly rate as a proxy for expected interest rates in his portfolio study of the life assurance companies but his results were unsatisfactory.
Kiernan (1978) used an extrapolative measure of interest rate expectations in his equation to explain the holdings of government securities by the private sector. The term included is:
The parameter estimates on  are significant and do not reject the restriction that the coefficients of rt and rt−1 should be of opposite sign. The positive sign on
are significant and do not reject the restriction that the coefficients of rt and rt−1 should be of opposite sign. The positive sign on  is, however, surprising since one would expect agents to reduce their holdings of securities if they expected rates to rise.
is, however, surprising since one would expect agents to reduce their holdings of securities if they expected rates to rise.
Johnston and Perrin (1978) in work for the N.I.F. model tried the inflation rate and the two quarter change in the commercial bill rate as sources of information used by the household-corporate sector in determining their interest rate expectations. They did not find any supporting evidence.
3.1.5 International Issues
i) Financial Market links
Little attention has been paid to the influence of foreign financial markets on the Australian scene. RBA76 and RBF detect a role for the Euro-dollar rate directly affecting short term (two year bond rate and 90 day commercial bill rate respectively) interest rates.
In RBA76, the 10 year U.S. bond rate adjusted for exchange rate expectations is the competing rate in expressions for the demand for money, and government securities and the supply of bank advances, whilst the Euro-dollar rate adjusted for exchange rate expectations is the competing rate in the expression for net Australian capital owned by overseas residents.[17]
ii) Capital Flows
In an important study using data for the 1960's and early 1970's, Porter (1974) specified a theoretical model of asset demands, which integrated foreign and domestic capital markets. Expressions for the domestic demand for money, domestic bonds and foreign bonds are specified where the explanatory variables are domestic income, domestic wealth, domestic and foreign interest rates, and an exchange rate risk factor. These expressions are combined with an equation for the foreign demand for domestic bonds. The model is closed with domestic money market and bond market equilibrium conditions and identities for the money supply and net capital flows. The authorities are assumed to determine the domestic component of the monetary base which is exogenous. Other exogenous variables in the system are domestic income, prices; price expectations and the current account balance, whilst all foreign variables with the exception of foreign demand for domestic bonds are exogenous.
Porter manipulates his theoretical structure to obtain a “reduced form” equation for net capital inflow, where the “exogenous” explanatory variables are income, wealth, the current account balance and the domestic component of the monetary base. Using data for 1961(3) – 1972(4) Porter estimates the reduced form equation to obtain the result that over the sample period 48% of any change in the domestic component of the monetary base would immediately be offset by capital flows. An important characteristic of the model which helps to explain the expected signs of each of the variables in the reduced form equation is the imposition of money market equilibrium. It is argued that when equilibrium is disturbed, capital flows (on the supply side) and domestic market interest rates (on the demand side) adjust to restore equilibrium. (The equivalent equation for the market interest rates has not been estimated because appropriate data is not believed to be available. Consequently, there is no evidence as to how rapidly the (unobservable?) market interest rate adjusts to help restore money market equilibrium.)
A problem with Porter's results is in his (necessary) assumptions regarding the exogeneity of prices, income, and the current account balance. The full model studies are will placed to relax these assumptions and consequently to test Porter's conclusions in a more general framework.
The asset demand equation in RBA76 are specified with similar explanatory variables to Porter's theoretical model. However, in contrast to the Porter model, money market equilibrium is not imposed in this model. A behavioural equation for net capital inflow is also estimated. The constraint variable in the equation is domestic income. This may be inappropriate for, as Porter points out, a structural net capital inflow equation should contain the two separate domestic and foreign demand expressions for domestic assets.
Jonson, Rankin and Taylor (1977)[18] test five alternative models of the interaction of money and the balance of payments in the framework of RBA76. On the basis of sample fit, the preferred model includes a structural model of capital flows (similar to Porter's theoretical model) with some evidence for a direct spillover for flow disequilibrium in the money market. The parameter estimates, however, suggest that the model is relatively closed in that the direct impact of excess money appears, in the short-run to fall more on domestic variables than on the balance of payments. This property is repeated for later versions of the model[19] where the excess money term is dropped from the capital flows equation.
On the issue of adjustment in the money market, Jonson, Rankin and Taylor (1977) estimate that the speed of adjustment of money balances is about five quarters. This estimate, however is based on a parameter derived from the flow disequilibrium term in the capital flows equation. As discussed above, other versions of RBA76 which do not include the flow disequilibrium term can only estimate the speed of adjustment of the residual asset (money) by appropriately designed simulation experiments.
iii) The exchange rate
With the exception of RBA76, the exchange rate is exogenous in each of the model studies. In RBA76, the exchange rate is modelled as a policy reaction function.
In the long-run it adjusts to restore purchasing power parity with the U.S. (although the lag is considerable), whilst the rate of unemployment, the proportional deviation between foreign reserves and money, and the rate of change of foreign reserves, are short-run explanatory variables. Two dummy variables for the U.S. devaluation in 1973 and timing of other exchange rate changes are also included in the equation. Significant coefficients are estimated for all variables with the exception of the unemployment rate.
This equation is not the best one in the RBA76 model. The lack of variance in the exchange rate series makes it difficult to estimate satisfactory statistical models for such a series. The advantage of the equation is that it may ensure more realistic long-run simulation properties for the model. In some simulation exercises, it may be of use to vary the values of the parameters in the exchange rate equation to ensure faster adjustment and greater sensitivity to short-run influences.
iv) Exchange rate expectations
As with the interest rate, in determining the effect of the exchange rate on real and financial markets, it is also necessary to measure the impact of exchange rate expectations. Porter (1974) found a significant role for expectations in determining capital flows. A threshold effect from holdings of international reserves was used. Once the domestic stock of international reserves reached a particular threshold level, this triggered expectations of a change in the exchange rate. Porter found that varying this threshold value between $1,700m and $2,400m for the period 1971(1) to 1972(4) did not significantly affect the parameter estimates. This is an interesting way of measuring exchange rate expectations which, in a full model framework, lends itself to endogenising these expectations.
RBA76 also measures exchange rate expectations. Two separate terms are used:
- a synthetic variable which increases (decrease) geometrically during the periods preceding a revaluation (devaluation). This sort of variable, which was first suggested by Black (1972), is designed to capture short-run fluctuations in exchange rate expectations.
- theratio of domestic to foreign prices adjusted for the current exchange rate. Given the slow adjustment speed which is estimated in the policy reaction function for the exchange rate, this term is expected to capture long-run exchange expectations.
Both exchange rate expectation terms are included in the domestic asset demand equations in RBA76. They play a stronger role in the capital flow and domestic bond equation than the money demand equation. It would be much more satisfactory if the short-run expectations term could be explained within the model. The approach used by Porter offers some promise here.
Short-run expectations can play an important role in speeding the adjustments in the RBA76 model. Jonson (1979) simulates a government expenditure impulse which is accompanied by strong expectations of a devaluation. The result is a very strong initial offset of the monetary impact through a leakage of reserves. This result, which is of the order of magnitude found by Porter, suggests that, even in a model where money markets do not clear instantaneously, and exchange rate movements are endogenised, it is still possible to generate the large offsets found by Porter if short-run exchange rate expectations are sufficiently volatile. The crucial issue which this study has not addressed is measuring the endogenous component of short-run exchange rate expectations.
3.1.6 Inconsistencies
Some of the major differences in approach have been discussed under other headings. In this section other, less fundamental, differences are discussed.
- the constraint variable chosen for desired stocks of financial assets by the corporate-household sector in RBA76, RBF, and the Melbourne Institute model is nominal gross domestic product.[20] Consequently, a desired stock level is assumed to be constrained by a flow variable. (Presumably this is in each case proxying wealth or permanent income.) A more appropriate constraint variable is chosen in RBAI where desired stocks are related to permanent income. Only the NIF model relates desired stocks to the total value of the portfolio.
-
trading bank overdraft limits play an important role in the NIF model of the corporate-household sector. This variable is included for the dual reasons of representing an important source of investable funds and capturing the relative importance within this sector of the corporate group. (This approach follows the work of Valentine (1973) where specific “distributional” variables were used in his study of the very liquid asset portfolio of the corporate-household sector.) Because of these dual effects the expected sign of this term is not always clear. The estimated sign of the term seems to be dominated by its role as a proxy for the importance of the corporate sector. Significant negative coefficients are found in the household deposits, government securities and cash and coin equations, whilst a significant positive coefficient is found in the fixed deposit equation. The significant negative coefficient in the money market deposit equation appears, however, to be inconsistent with the interpretation of the role of this term. Along with various interest rates and the constraint variable (the total portfolio size) total bank overdraft limits play a significant role in all financial asset equations. The importance of the term in the government securities equation is highlighted when the sample fit of the estimated equation is compared to the equation when overdraft limits are kept on trend after 1972. The large reduction in holdings of government securities during 1973 and 1974 is not captured in the latter case. It is suggested that the overdraft limits term could also be proxying interest rate expectations.
Because overdraft limits are supply determined, these interest rate expectations are assumed to be those of the trading banks. However, there is no evidence in the model's explanation of the trading banks portfolio behaviour that interest rate expectations affect either overdraft limit approvals or holdings of government securities. At present it is not clear that a convincing explanation of the importance of trading bank overdraft limits in the NIF model has been made. Indeed, the possibility that this variable is proxying the more theoretically robust spillover effects which were found in the sectoral studies should be investigated.
- the estimated behaviour of the residual asset (trading bank demand deposits) in the NIF model is not consistent with the properties of the residual asset in other studies. A rise in the value of the portfolio leads to a fall in the holdings of demand deposits. (Johnston and Perrin (1978)).
- as discussed in section 1, the treatment of the determination of bank deposits and bank holdings of liquid assets is fairly standard across the studies. Bank deposits are determined by the household-corporate sector and the liquid assets of the banking sector are the residual in the banking sectors balance sheets. The treatment of bank advances is not so consistent. NIF and the Melbourne Institute draw on an innovative study by Valentine (1973)[21] and treat bank advances as the outcome of the supply decision for bank approvals and of the demand decision for drawings (and in the case of savings banks, the rate of repayment) RBF treats both trading and savings bank advances as supply determined, whilst RBAI has trading bank advances (apart from mortgage approvals) demand determined and savings bank mortgage approvals supply determined. RBA76, on the other hand, combines demand and supply influences in a single “mixed” equation with the demand influence being proxied by nominal gross domestic product relative to trend. Later versions of RBA76 (see Jonson, Evans and Moore (1978)) use monetary disequilibrium as a demand proxy. The critical test of whether supply or demand influences prevail on trading bank advances is the sign on the coefficient on the advances rate in the net advances equation. Curiously, the signs on the advances rate in RBF and RBAI are both statistically significant but opposite. Although the use of a slightly different interest rate series may explain some of this difference the most logical explanation is in the data periods. Unlike RBAI (1959(1) – 1969(4)) the RBF sample (1959(3) – 1975(3)) spans the early 1970's when excess demand effects may have been much stronger. The best resolution of this apparent conflict would be, however, the Valentine approach, where the interaction of supply and demand influences determines the level of outstanding advances. A closer analysis of these estimates may reveal that demand and supply were alternatively dominant over the sample period.
- Another difference in the treatment of bank advances is that, whereas those studies which model net advances in a single equation find strong evidence for interest rate effects all the studies which model separate equations for approvals and drawings find no evidence for interest rates affecting approvals.
- As shown in Table 2, the residual asset for the non-bank groups in the Melbourne Institute model includes trading bank fixed deposits whilst trading bank current deposits are determined by a separate demand equation. This is inconsistent with the other studies where, for the particular degree of disaggregation, the asset with the lowest adjustment costs is chosen as the balance sheet residual. Some indication that current deposits should be the residual asset comes from the slow own adjustment speed which is found for the estimated current deposits equation, (see Table 5). This speed of adjustment is slower than other studies find for fixed deposits (see Table 4), suggesting that, consistent with the expected properties of a residual asset, current deposits respond to other asset disequilibria and total portfolio changes rather than their own disequilibrium.[22]
| Study |
Sample period | Income measure | Interest rates | Long run elasticity of demand with respect to |
Adjustment within 1 year |
Other Factors |
|
|---|---|---|---|---|---|---|---|
| Income | Interest rates | ||||||
| Deane (1969) | 1960(3)–1969(2) | Permanent GNP | r2 | 0.92 | 0.86 | 38% | Government domestic borrowing; price expectations change in bank advances |
| rfd,m | −0.79 | ||||||
| Norton and Henderson (1971) |
1959(1)–1969(4) | Permanent GNP | r10 | 0.40 | 0.22 | 81% | Government domestic borrowing; price expectations |
| rfd,2 | −0.24 | ||||||
| Jonson (1972) | 1957(4)–1971(4) | GNP | r10 | 0.72 | 0.60 | 52% | Government domestic borrowing; price expectations capital gain expectations |
| Jonson, Moses and Wymer (1976) | 1959(3)–1974(4) | GDP | r10 | 1.0* | 0.57 | 40% | Exchange rate** expectations world interest rate |
| rus,10 | −0.59 | ||||||
| Kiernan (1977) | 1959(4)–1975(4) | GDP | r2 | 0.52 | 2.23 | 18.5% | Price expectations change in the liquidity base |
| rfd,m | −1.88 | ||||||
| Johnston and Perrin (1978) | 1966(2)–1977(2) | r2 | 0.76 | 71% | Overdraft limits | ||
| rfd,1−2 | −0.74 | ||||||
|
* Constrained; |
|||||||
| Study |
Sample period | Income measure | Interest rates | Long run elasticity of demand with respect to |
Adjustment within 1 year |
Other Factors |
|
|---|---|---|---|---|---|---|---|
| Income | Interest rates | ||||||
| Kortor., Cohen and Sweeny (1970) | 1959(1)–1968(4) | Permanent gross national product | rfd,1 | 1.70 | 0.36 | 68% | Domestic official borrowing |
| Valentine (1973) | 1962(4)–1969(4) | GDP | rfd,1 | 0.95 | 0.36 | 83% | |
| Kiernan (1977) | 1959(4)–1975(4) | GDP | rfd,m | 1.34 | 0.35 | 60% | Change in the liquidity |
| r2 | −0.32 | ||||||
| Kiernan (1978) | 1960(2)–1976(2) | GDP | rfd,m | 1.39 | 0.92 | 49% | |
| Johnston and Perrin (1978) | 1966(2)–1977(2) | – | rfd,1−2 | – | 0.77 | 73% | Overdraft limits |
| r2 | −0.79 | ||||||
| Study |
Sample period | Income measure | Interest rates | Long run elasticity of demand with respect to |
Adjustment within 1 year |
Other Factors |
|
|---|---|---|---|---|---|---|---|
| Income | Interest rates | ||||||
| Norton, Cohen and Sweeny (1970) | 1959(1)–1968(4) | GDP | rfd,1 | 0.73 | −0.44 | 56% | Domestic official borrowing |
| Derody and Sheahan (1977) | 1961(2)–1975(2) | GDP | r2 | 1.76 | −1.77 | 34% | |
| Kiernan (1977) | 1959(4)–1975(4) | GDP | r2 | 0.70 | −0.78 | 37% | Change in the liquidity base |
| Johnston and Perrin (1978) | 1966(2)–1977(2) | GDP | – | 0.30 | residual | Overdraft limits | |
| Study |
Sample period | Income measure | Interest rates | Long run elasticity of demand with respect to |
Adjustment within 1 year |
Other Factors |
|
|---|---|---|---|---|---|---|---|
| Income | Interest rates | ||||||
| Norton, Cohen and Sweeney (1970) | 1959(1) – 1966(4) | GNP | rfd,1 | 0.62 | −0.24 | 43% | Domestic official borrowing |
| Norton and Henderson (1971) | 1959(2) – 1969(1) | GNP | rfd,1 | 0.49 | −0.75 | 17% | Domestic official borrowing |
| Derody and Sheahan (1977) | 1961(2) – 1975(2) | GDP | r2 | 1.07 | −0.34 | 31% | |
| Kiernan (1977) | 1959(4) – 1975(4) | GDP | – | 0.62 | – | 49% | – |
| Johnston and Perrin (1978) | 1966(2) – 1977(2) | GDP | – | 1.01 | – | full adjustment within a quarter | Overdraft limits introduction Of ASB's. |
| Study |
Data | Income measure | Interest rates | Long run elasticity of demand with respect to |
Adjustment within 1 year |
Other Factors |
|
|---|---|---|---|---|---|---|---|
| Income | Interest rates | ||||||
| Kiernan (1977) | 1959(4)–1975(4) | GDP | rsb | 0.79 | 1.08 | 15% | Change in liquidity base |
| Johnston and Perrin (1978) (including building society deposits) | 1966(2)–1977(2) | GDP | – | 0.19 | 93% | Overdraft | |
| Norton and Henderson (1971) | 1959(1)–1969(4) | GNP | rsb | 1.16 | 1.65 | 12.6% | – |
| r10 | −2.26 | ||||||
| Study |
Data | Income measure | Interest rates | Long run elasticity of demand with respect to |
Adjustment within 1 year |
Other Factors |
|
|---|---|---|---|---|---|---|---|
| Income | Interest rates | ||||||
| Norton, Cohen & Sweeney (demand) | 1958(4) – 1969(3) | Permanent gross national product | ra | 1.18 | −0.71 | 72% | Domeatic official borrowing Reserve Bank lending requests |
| r2 | 0.28 | ||||||
| Norton and henderson (1971) (demand) | 1959(1) – 1969(4) | Permanent gross national product | ra | 1.06 | −0.63 | 79% | Domeatic official borrowing Reserve Bank lending requests |
| r2 | 0.27 | ||||||
| Jonson, Moses and Wymer (1976) (supply) | 1959(3) – 1974(4) | Free deposits | r10 | 1.0* | −0.22 | 76% | Exchange rate expectations required reserve ratios.Reserve Bank lending requests capital inflow controls demand effects** |
| rus,10 | 0.20 | ||||||
| Kiernan (1977) (supply) | 1959(4) – 1975(4) | Free deposits | ra, wa | 0. 99 | 0.36 | 61% | Reserve Bank lending requests growth in GDP relative to trend |
|
* Constrained |
|||||||
| INTEREST RATE KEY | |
| rsb: | rate on savings bank deposits |
| rfd, 1: | rate on fixed deposits with 1 year term |
| rfd, 2: | rate on fixed deposits with 2 year term |
| rfd, 1−2: | rate on fixed deposits with 1–2 year term |
| rfd, m: | maximum rate on fixed deposits |
| r2: | theoretical yield on Australian Government securities with 2 years to maturity |
| r10: | theoretical yield on Australian Government securities with 10 years to maturity |
| rUS, 10: | theoretical yield on US Government securities with 10 years to maturity |
| ra: | maximum rate on advances of all trading banks |
| ra, wa: | weighted average rate on advances of major trading banks. |
3.2 Some detailed results
3.2.1 Parameter estimates
Tables 3–8 compare long-run income and interest rate elasticities and speeds of adjustment in the full scale econometric models for the household-corporate sector. In each case the relevant interest rates are listed and other important variables noted. Points of interest from the tables are:
- a fixed deposit rate and a bond rate are generally used as competing rates in government security and fixed deposit demand equations;
- income elasticities and partial equilibrium speeds of adjustments are generally higher for fixed deposits than current deposits or currency;
- income elasticities for government security holdings appear to fall as the sample goes further into the 1970's;
- interest rate elasticities for government securities and fixed deposits have generally risen as the sample goes into the 1970's.
3.2.2 The Role of Direct Monetary Policy Instruments
i) Required reserve ratios of the trading banks
Johnston finds from his parameter estimates that a change in the SRD ratio has an immediate impact on the holdings of government securities and money market deposits by the trading banks. Advances respond with a mean lag of between one and two quarters. Evans (1979) examines the dynamic simulation properties of RBA76 in response to a change in the SRD ratio. It was also found that the initial impact of the change impinged on the trading banks' holdings of liquid assets. This was followed by a strong increase in the commercial bill rate as the banks enter the money market to bid for deposits in order to protect their holdings of outstanding advances. The results of the analysis suggest that changes in the SRD ratio have a less certain impact on trading bank advances than claimed by Johnston.
ii) Bank lending guidelines
Norton and Henderson use dummy variables which identify two separate effects of official lending guidelines on trading bank lending. These represent requests to restrict advances outstanding and requests to moderate the rate of new lending. The requests are found to be slow to have an impact, taking 3 to 4 quarters. The significance of these variables is confirmed by the later studies of Valentine, RBA76, Derody and Sheahan and RBF (although in some cases the sample period did not cover the time of the requests to restrict advances outstanding). Johnston finds evidence for a dummy covering the June quarter 1974 to the June quarter 1976, a period during which it is claimed the Reserve Bank sought substantial restraint on new lending. This variable, however, enters without a lag. It is suggested that this implies something about “the severity of the requests”.
3.2.3 Simulations
One of the most neglected areas in financial model building is an examination of the dynamic simulation properties of the models. These properties are not adequately examined in single sector studies since important variables must be made exogenous. The relevant full model simulation studies[23] which are available mainly relate to RBAI and RBA76.[24]
i) RBAI and RBA76 – a comparison
Table 9 compares the response of RBA1/74 and RBA79[25] to a sustained increase in real government spending of around $50m per quarter, from the first quarter of 1967 and the third quarter of 1966 respectively. In both cases, the figures represent deviations from the respective control solutions.
| Quarters elapsed | 1 | 4 | 8 | 16 | 24 | 27 | |
|---|---|---|---|---|---|---|---|
| Real activity($m) | RBA1/74 | 43 | 74 | 85 | 95 | 77 | 68 |
| RBA79 | 0 | 46 | 65 | 53 | 25 | 19 | |
| Inflation (% pa) | RBA1/74 | 0 | 0 | 0.2 | 0.3 | 0.4 | 0.4 |
| RBA79 | 0 | 0.3 | 0.7 | 0.6 | −0.2 | −0.4 | |
| Volume of money ($m) | RBA1/74 | 19 | 80 | 156 | 313 | 511 | 605 |
| RBA79 | 25 | 70 | 77 | 39 | −250 | −343 | |
| Foreign Reserves ($m) | RBA1/74 | −3 | −19 | −59 | −165 | −325 | −398 |
| RBA79 | 4 | −49 | −136 | −295 | −463 | −460 | |
| wealth ($m) | RBA1/74 | 173 | 918 | 1,317 | 1,883 | 3,264 | 2,994 |
It is interesting to compare the properties of the two models.
- in both models there is a positive initial effect on real activity. The impact effect on output is much stronger in RBA1/74. This reflects the fact that output is, (subject to capacity constraints), demand determined in RBA1/74, whilst in RBA79 it is supply determined with inventories playing the buffering role. In both models the stimulus to output starts to be offset after 3 or 4 years. This process seems to work somewhat more quickly in RBA79.
- in both models there is a strong initial build-up in money balances following the increase in government spending. This reflects the residual asset role of money as discussed in Sections 3.1.1 and 3.1.2. The build-up in money is much more short-lived in RBA79 than in RBA1/74. This is, in part, explained by the faster loss of reserves and the more rapid response of taxation to the initial rise in income in RBA79. Furthermore, the monetary disequilibrium term in the equation for non-bank holdings of government securities seem to lead to a more rapid diversification of portfolio than in the case of RBA1/74. These simulation properties illustrate the point made in Section 3.1.3, that although the short-run properties of the financial sectors of the two models can be expected to be similar, the long-run properties may vary substantially.
- the effect on inflation is much stronger and occurs much more quickly in RBA79 than in RBA1/74. This mainly reflects the role of excess money balances in the price equation in RBA79.
- it is interesting to note that the stimulus to real activity begins to fall back by the fourth year in RBA1/74. This is despite a continued substantial rise in wealth. Such results suggest that the links in RBA1/74 between wealth and real activity may not be very strong.
- the rapid build up in wealth shown in RBA1/74 is perplexing. It must be open to serious doubt whether sustained increases in government spending could cause such a rise in wealth, and there appears to be scope for altering the treatment of wealth in this model. Some suggestions include endogenising interest rates and discounting future tax liabilities in the way suggested by some authors.[26]
ii) RBA76/79 – some more results
More detailed simulation studies have been carried out with RBA76. Several of these appear in the second paper in Norton (ed.) (1977), further results are presented by Eberhardt, Rankin and Taylor (1978), Evans (1979), and Jonson and Trevor (1979).
These studies produce broadly similar results to those discussed above. Eberhardt, Rankin and Taylor impose a 10 per cent proportional interest rate reduction. The properties of the model illustrate an important implication of the residual asset role for money. The reduction in the interest rate leads to a fall in the desired levels of other financial assets. This leads to a change in the excess holdings of these assets, causing money holdings to rise quickly. The rise in money then leads to a sustained effect on prices in a similar way to that noted for the government expenditure impulse.
In a study using a more disaggregated financial sector within the RBA76 model, Evans tests the ability of the authorities to control the money supply following a sustained 10 per cent increase in real government expenditure. The results suggest that, in the short-run, policies impinging on the required asset ratios of the banks are ineffective whilst interest rate policies are effective. However, full control of money was not possible for 2 to 3 quarters. This was achieved with a rise in the long-term bond rate of about 0.5 per cent.
Jonson and Trevor analyse the effects of a wide range of shocks in RBA79. This study also illustrates that, for the shocks considered, money can be controlled within a year by suitable variations in interest rates. This control has substantial benefits for inflation in the medium-run, although in the short-run there appears to be little that any of the three rules for monetary policy which are considered can do to offset the direct effects of the shocks.
Footnotes
The RBA76 model has been updated since the original study. Relevant references are given below. [9]
The financial sector models discussed in these two studies have not yet been linked to the full N.I.F. model. [10]
RBA1 does not explicitly include a formation table identity. Instead an identity for the government borrowing requirement is used. The structure of RBA1 is discussed further in section 3.1.2. [11]
Shaw's results must be open to considerable doubt since he finds that the long-run effect of a rise in total assets is for the life assurance companies to increase their holdings of liquid assets above the impact level. As discussed above, Sharpe finds the (more plausible) opposite result. [12]
Laidler (1979) provides some evidence using a single equation study of U.S. data that monetary disequilibrium plays a significant role in the U.S. consumption function. [13]
The demand for the residual asset can be expected to adjust much more slowly than the supply. [14]
Monetary disequilibrium has recently been added to the expenditure equations in the real sector of RBF although the parameter estimates are fairly low. [15]
This model, which is a updated version of RBA76, is discussed in Jonson and Trevor (1979). Earlier versions of RBA76 include nominal interest rates in the household expenditure equation. [16]
The original version of RBA76 included the 10 year bond rate in the equation for capital inflow. Later versions, see Jonson, Evans and Moore (1978) have the specification described above. [17]
See also pp 79–85 of Norton (ed.), (1977). [18]
See Eberhardt, Rankin and Taylor (1978) and Jonson and Trevor (1979). [19]
Trevor (1978) introduced a permanent income measure into the expenditure and asset demand expressions into a version of RBA76. He found that this speeded up the government security and capital flow adjustments, although it generated surprisingly high estimates of the adjustment parameter for monetary disequilibrium in the price equation. [20]
Both these models use flow adjustment model rather than stock adjustment as used by Valentine. [21]
Note that some evidence to the contrary here comes from the Parkin et al (1976) study which shows current deposits adjusting relatively rapidly. [22]
The simulation properties of the NIF model which incorporate the financial sector discussed above have not yet been made available. For the simulation properties of the NIF model with a limited financial sector see Higgins and Caton (1977), Coghlan (1978). FitzGerald and Higgins compare the properties of the model with RBA76 in Norton (ed.) (1977) pp. 176–215. [23]
Derody and Sheahan (1977) performed a simulation analysis on the Melbourne Institute model from which only limited results were published. The results, however, demonstrated the strong impact influence which changes in the level of foreign reserves will have on the volume of money. Such a result would be difficult to duplicate in single equation studies which treat the volume of money as demand determined. [24]
These models are updated versions of RBA1 and RBA76, respectively. The essential financial sector features of the original models, as discussed in earlier sections of this paper, have, however not been changed. For more details of the updates and the simulation experiments see Norman and Henderson (1974), Norman and Moses (1975), for RBA1/74 and Jonson and Trevor (1979) for RBA79. [25]
See Barro (1974). [26]