RDP 7904: Some Aspects of RBA76 and RBF1 2. Some Aspects of RBA76(T)
September 1979
2.1 The Model Under Consideration
The specification of RBA76(T) (where “T” denotes testing) was developed by Eberhardt, Rankin and Taylor (1978) as part of the process of testing the suggestions for changes in the specification of RBA76 made at the 1977 Conference in Applied Economic Research.[4] The estimates differ from those given below for the same period as the convergence tolerance in the estimation programme was set at the default setting of 0.1% change in parameters in successive iterations in the present study. The additional iterations result in some improvement to the within sample dynamic simulation performance but the response of the model to a government expenditure shock changes considerably. Eberhardt et al conclude that:
“… the specification revisions which are incorporated in the current version of the model seem to have had a beneficial effect on its simulation properties; ‘implausible’ and ‘paradoxical’ system responses to the various shocks have, in the main, been eliminated …”[5]
This conclusion does not apply to the version of the Eberhardt et. al. model used in this paper. In fact, some model responses reported below are highly implausible and hence the results should not necessarily be applied to other published versions of RBA76.[6] The procedure followed in this paper is to generate results mechanically and not to respecify the model on the basis of implausible results.
2.2 Parameter Stability
In any modelling project the issue of parameter stability arises.[7] This issue is important as it may confirm or refute the existence of identified channels of behaviour or the possible absence of others.
Parameter stability is a function of:
- data revisions,
- changes in the quality of data through time,
- changes in estimation technique,[8]
- changes in model specification,[9]
- inappropriate model specification, or
- shifts in the structure of the economy over time that have not or cannot adequately be captured in the specification.
It is difficult to identify the sources of parameter instability when a combination of the above factors is operating. By making the assumption that the quality of data has not changed through time[10] it is possible to design experiments where the only variable factors are points (v) and (vi). Isolating these factors is achieved by taking a version of RBA76 and estimating this model (using a consistent set of data) with the same estimation technique when the only variable factor is the length of the sample period.[11]
The version of the model used in this analysis is given in Appendix A. This model is estimated[12] according to this specification over the following periods:[13]
- 1959(3) – 1975(4) (estimates denoted EST754), and
- 1959(3) – 1976(4) (EST764).
For the following estimation periods it is necessary to “alter” the model's specification.
- 1959(3) – 1971(3) (EST713),
- 1959(3) – 1972(4) (EST724),
- 1959(3) – 1973(4) (EST734), and
- 1959(3) – 1974(4) (EST744).
Alteration of the model's specification is a result of two factors.[14] First, various dummy or synthetic variables used in the model are not relevant over all or part of the period 1971(3) to 1974(4).[15] Second, for the estimates to 1971(3) the exchange rate ($US/$A) is fixed and hence this variable is exogenised.[16] Further, it is assumed that the fixed exchange rate also leads to a change in the role of exchange rate expectations. In particular it is assumed that exchange rate expectations are passive over this period hence their implicit treatment[17] is dropped from the various asset,export, import and output equations.
The initial values for the parameter set were standardised at realistic values for all seven estimation periods and the convergence tolerance was set at its default level. For the estimates to 1973(4), 1974(4), 1975(4) and 1976(4) this resulted in convergence after 43, 62, 76 and 20 iterations respectively.
Problems with convergence occur for the estimation periods ending at 1971(3) and 1972(4). In both cases the coefficients β2 and β9 on Dlog P in the expenditure and investment equations oscillate wildly. Consequently these parameters are constrained at near zero values of .001 and −.001 respectively. In addition, for the estimation period to 1972(4) the interest elasticity (β25) becomes large and the adjustment speed (α14) converges to zero in the advance equation. For expediency the adjustment speed in this equation (α14) is constrained to .1 – this being the estimate for this parameter from the estimation period ending in 1973(4). The interest elasticity then estimates satisfactorily.[18]
For the sample period ending in 1971(3) this same problem occurs in the capital flows equation as well as in the advances equation. Again for expediency the adjustment parameters (α13 and α14) are constrained to the estimates from the sample period ending in 1973(4). With these changes the estimates for the period ending in 1971(3) converge in 40 iterations. For the estimates to 1972(4) absolute convergence is not obtained even though the log likelihood value stabilises. The cause of this appears to be with σ24 the coefficient on the Dlog R term in the exchange rate reaction function. In essence there are little data on which this parameter can be well determined. Consequently, for this sample period ending in 1972(4), the near stationary estimates are used. Parameter estimates and standard errors for the various estimation periods are given in Appendix B.
2.3 Some Preliminary Observations
The number of parameters estimated ranges from 51 for the shortest to 71 for the longest sample period. An attempt was made to hold constant the structure of the model over these alternative estimation periods. As discussed above, convergence is not possible for the two shortest periods unless some changes to the model are made. However, the structure of the model is not changed when particular parameters change sign or show evidence of instability.
The approach taken in following subsections is to take the estimates to 1975(4) as a base for comparison as this is the period over which RBA76 was developed. In the section below analysing parameter stability for the RBF1 model the parameter estimates to 1971 are considered to be a base as this was the main sample period for that model's development.[19]
2.4 Analysis of Parameter Stability
To test statistically the equality between the parameter estimates from the 1959(3)–1975(4) period and any of the alternative periods requires not only the variance of the individual estimates but also covariances between the corresponding estimates. The latter covariances between estimation periods are not readily available hence it is necessary to make a somewhat ad hoc examination of parameter stability.
First, it is possible to test the null hypothesis that the alternative estimates are equal to the estimates to 1975(4) on the assumption that the estimates to 1975(4) are predetermined; that is, the estimates to 1975(4) are considered to be the true population values. This is considered in Section 2.4.1 below.
Second, the null hypothesis that the alternative estimates are equal to the estimates to 1975(4) can be tested under the assumption that the covariances between the two sets of estimates are zero.[20] This is considered in Section 2.4.2 below. It is assumed in this paper that rejection of the null hypothesis is associated with parameter instability.
Section 2.4.3 considers three other factors: how parameter estimates vary in absolute size, whether there are any significant changes in parameter signs, and the number of parameters insignificantly different from zero.
2.4.1 Tests of Equality between Parameter Estimates and Population Values (EST754 assumed equal to population)
Table 1[21] summarises the results of assuming that the estimates to 1975(4) are the true population values and then testing the null hypothesis that the estimates for alternative periods are equal to the population values.[22]
The results indicate that the null hypothesis is rejected[23] for a minimum of 21% of the parameters – this occurring for the estimates ending in 1976(4), that is, with the data for one additional year.[24] Further, the proportion of parameters that is rejected as being equal to the population values in general increases as the sample size diverges from the base period. The exception here is the estimates to 1972 (4) which have the maximum proportion (58%) of parameters that fail the test,[25] this being slightly higher than the proportion (55%) for the estimates to 1971(3).
| Parameter Group | Number of Parameters | Number (and proportions) of Parameters Where the Null Hypothesis is Rejected | ||||
|---|---|---|---|---|---|---|
| EST713 | EST724 | EST734 | EST744 | EST764 | ||
| Main Adjustment Parameters (α's) |
21 |
9 (43%) |
12 (57%) |
9 (43%) |
8 (38%) |
3 (14%) |
| Monetary Disequilibrium Parameters (γ's) |
4 |
4 (100%) |
3 (75%) |
2 (5o%) |
– |
1 (25%) |
| Stocks Disequilibrium Parameters (ν's) |
4 |
– |
– |
1 (25%) |
– |
1 (25%) |
| Other Adjustment Parameters (σ's) |
14 |
9 (64%) |
9 (64%) |
5 (36%) |
5 (36%) |
4 (29%) |
| Equilibrium Parameters (β's) |
||||||
| – Relative Prices | 7 |
4 (57%) |
4 (57%) |
1 (14%) |
2 (29%) |
2 (29%) |
| – Other | 3 |
3 (100%) |
3 (100%) |
2 (67%) |
3 (100%) |
– (0%) |
| Total | 53 | 29 (55%) |
31 (58%) |
20 (38%) |
18 (34%) |
11 (21%) |
| Parameter Group | Number of Parameters | Number (and proportions) of Parameters Where the Null Hypothesis is Rejected | ||||
|---|---|---|---|---|---|---|
| EST7I3 | EST724 | EST734 | EST744 | EST764 | ||
| Main Adjustment Parameters (α's) | 21 |
10 (48%) |
9 (43%) |
4 (19%) |
6 (29%) |
4 (19%) |
| Monetary Disequilibrium Parameters (γ's) | 4 |
1 (25%) |
3 (75%) |
1 (25%) |
– | 1 (25%) |
| Stocks Disequilibrium Parameters (ν's) | 4 |
– | – | 1 (25%) |
– | – |
| Other Adjustment Parameters (σ's) | 14 |
8 (57%) |
9 (64%) |
4 (29%) |
4 (29%) |
– |
| Equilibrium Parameters (β's) | ||||||
| – Relative Prices | 7 |
2 (29%) |
3 (43%) |
1 (14%) |
2 (29%) |
1 (14%) |
| – Other | 3 |
2 (67%) |
3 (100%) |
2 (67%) |
1 (33%) |
– |
| Total | 53 |
23 (43%) |
27 (51%) |
13 (25%) |
13 (25%) |
6 (11%) |
The parameter set can be divided into subsets according to various criteria. One division is given in Table 1, which divides the parameters into groups based on the parameter's function in the model. The same general trend noted above can be found for the various parameter subsets.
2.4.2 Tests of Equality between Parameter Estimates Assuming Covariances are Zero
As all the sets of estimates have a common sub-sample period (1959(3)–1971(3)) it is likely that the covariances between the alternative sets of estimates is non-zero and positive. However, there is great difficulty in measuring these covariances in practice (particularly given the size of the model), so the procedure followed here is to assume that they are zero. This assumption allows a test of stability to be conducted where the important assumption needed for the test in Section 2.4.1 – that is, that the estimates to 1975(4) are the population values – is avoided. The null hypothesis in this case is then whether the estimates from one of the alternative estimation periods are equal to the estimates to 197(C4), thus making use of the variances of both sets of estimates.[26]
The results for this test are summarised in Table 2. Under this test the null hypothesis is rejected for a minimum of 11% of the parameters, this again occurs for the estimates to 1976(4). The maximum rejection rate (51%) occurs again for the estimates to 1972(4). Also for the total number of parameters the size of the rejected set is well correlated with the size of the non-overlapping sample period (again the estimates to 1972(4) are the exception). This pattern is also repeated for most parameter groups.
2.4.3 Other Tests
Table 3 indicates the extent to which parameters from alternative estimation periods differ in an absolute sense from the estimates to 1975(4). Three ranges are identified: less than 50%, between 50% and 100%, and greater than 100%.
Similar trends to those found earlier are identifiable. Thus the greater is the non-overlapping sample period the greater is the proportion of parameters that differ in an absolute sense by more than 50%. It can be noted that the proportion of parameters which differ by more than 100% can also be large.
Even though there can be these large changes in the absolute value of parameters the number of significant changes in sign of parameters is small.[27] These results are given in Table 4. Associated with this test is the question of the number of insignificant parameters. As Table 5 indicates the proportion of insignificant parameters can be large.
| EST754 Parameters Plus or Minus | Number (and proportions) of Parameters | ||||
|---|---|---|---|---|---|
| EST713 | EST724 | EST734 | EST744 | EST764 | |
| Less Than 50% | 24 (45%) |
23 (43%) |
32 (60%) |
34 (64%) |
42 (79%) |
| Between 50% and 100% | 11 (21%) |
15 (28%) |
12 (23%) |
9 (17%) |
7 (13%) |
| Greater Than 100% | 18 (54%) |
15 (28%) |
13 (25%) |
10 (19%) |
4 (8%) |
| Number of Parameters | Number of Parameters that have Changed Sign | |||||
|---|---|---|---|---|---|---|
| EST713 | EST724 | EST734 | EST744 | EST764 | ||
| Main Adjustment Parameters (α's) | 21 | – |  |
– | – | – |
| Monetary Disequilibrium Parameters (γ's) | 4 | – | – | – | – | – |
| Stocks Disequilibrium Parameters (ν's) | 4 | – | – | – | – | – |
| Other Adjustment Parameters (α's) | 14 |  |
– | – |  |
– |
| Equilibrium Parameters (β's) | ||||||
| – Relative Prices | 7 | – | – | – | – | – |
| – Other | 3 | – | – | – | – | – |
| Total | 55 | 1 | 1 | – | 1 | – |
|
+ Indicates those that have changed from the correct signs (a priori) and significant in EST754 to the incorrect sign and significant. |
||||||
| Parameter Group | Number of Parameters | Number (and proportions) of Insignificant Parameters | |||||
|---|---|---|---|---|---|---|---|
| EST713 | EST724 | EST734 | EST744 | EST754 | EST764 | ||
| Main Adjustment Parameters (α's) | 21 | 5 (24%) |
3 (14%) |
3 (14%) |
3 (14%) |
1 (5%) |
– |
| Monetary Disequilibrium Parameters (γ's) | 4 | 1 (25%) |
1 (25%) |
2 (50%) |
1 (25%) |
– | – |
| Stocks Disequilibrium Parameters (ν's) | 4 | – | – | – | – | – | 1 (25%) |
| Other Adjustment Parameters (σ's) | 14 | 3 (21%) |
3 (21%) |
2 (14%) |
3 (21%) |
3 (21%) |
3 (21%) |
| Equilibrium Parameters (β's) | |||||||
| – Relative Prices | 7 | 1 (14%) |
2 (29%) |
2 (29%) |
3 (43%) |
1 (14%) |
1 (14%) |
| – Other | 3 | – | – | – | – | – | – |
| Total | 53 | 10 (19%) |
9 (17%) |
9 (17%) |
10 (19%) |
5 (9%) |
5 (9%) |
2.4.4 Summary of the Results of Various Tests
The various tests above each have similar implications. If we accept that rejection of the various null hypotheses can be associated with parameter instability then the results suggest that even for small changes in the sample period there is evidence of some instability. The experiments have been designed so that we can conclude that this instability is a result of inappropriate model specification and/or structural change to the economy. It is still not possible to determine which of these combinations is responsible.
2.5 Behaviour of Particular Parameters
The above subsections give evidence of parameter instability and two possible reasons for that instability. Such evidence can provide some useful and positive information rather than the negative connotations which occur at first sight. For example, it can suggest where a particular specification is currently inappropriate, or was inappropriate at some stage in the past, or can help in identifying when changes in the structure of the economy took place.[28]
As there is not sufficient space in this paper to consider the behaviour of all parameters, this subsection considers the behaviour of a small number of parameters and asks the question whether any useful information can be gained by analysing the time profile of these parameters.
The first parameters chosen for consideration are the monetary disequilibrium terms (γ's).[29] Figure 1 graphs the behaviour of these four parameters.[30] These parameters show noticeable trends. In the expenditure equation the monetary disequilibrium parameter (γ1) gets less negative while the reverse is true for the bonds equation (γ3). The monetary disequilibrium parameter in the price equation (γ2) also becomes increasingly negative. For advances (a negative asset) the monetary disequilibrium term (γ4) has at first an increasingly positive trend but this is reversed for the longest sample period.
One interpretation of the trends in γ1, γ3 and γ4 (the increasingly positive trend in γ4) is that the high saving ratio of the seventies may partly be explained by a shift in the behaviour of households. Householders' allocation of excess or unanticipated money balances appears to have shifted away from expenditure to financial assets over this period.
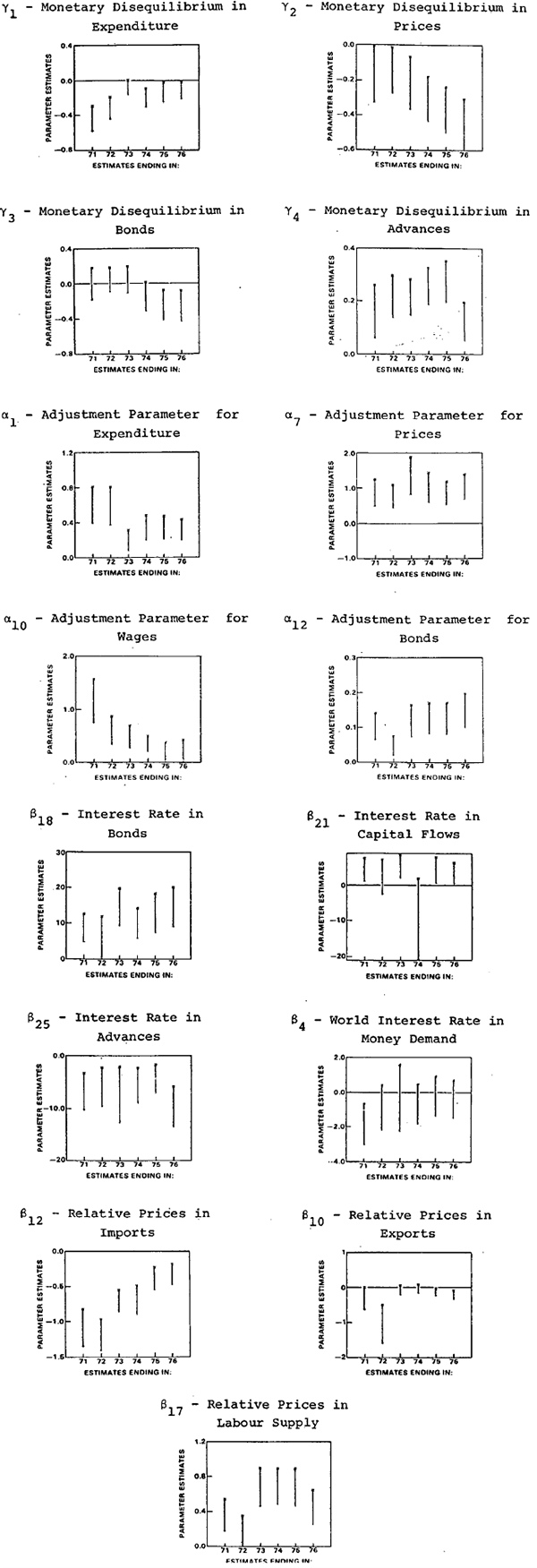
One interpretation of the role of monetary disequilibrium in the price equation is as a proxy measure for price expectations. Thus the trends in γ2 could be interpreted as reflecting the increasing importance of price expectations in the seventies.
Figure 1 also plots the behaviour of some other parameters. The behaviour of individual adjustment parameters varies considerably. The behaviour for four of these terms (α1, α7, α10 and α12) is shown in Figure 1. For some parameters there is a noticeable downward trend, for example, the adjustment speeds of expenditure (α1), wages (α10), employment (α3, 1) and indirect taxes (α16, 1, α16, 2). Others trend upwards: price of exports (α9), bonds (α12), interest rate (α17) and interest payments on debt (α19). Most other adjustment parameters show some volatility, the adjustment speed of prices (α7) for example is graphed in Figure 1.
As can be seen from Figure 1 interest rate parameters show some variability but do not have noticeable trends. Relative prices in imports (β12), exports (β10) and labour supply (β17) show more pronounced trends. Movements in some of these parameters may be associated with specific events. For example, the behaviour of relative prices in the export equation for the EST734 estimates may be linked with exchange rate policy. Also, relative prices in the labour supply equation for the estimates ending in 1973 and onwards may be linked with wages policy. Other trends such as that for the import relative price are difficult to explain.
Evidence such as this on parameter behaviour should be used to improve our research on macroeconomic models. For example, one avenue for research could be time dependent parameters or parameters which are a function of other variables.
2.6 Simulation Experiments
All the previous analysis has been in terms of individual parameters. The next question to ask is how these changes in parameters alter the characteristics of the model as a whole; that is, do the simulation behaviour and policy implications of a given model change when the data on which that model is estimated change. Two types of simulation experiments are considered. The first discussed in Section 2.6.1 looks at within and out of sample dynamic simulations for the different sets of estimates. The second experiment discussed in Section 2.6.2 looks at how policy implications of the model may change by analysing the multiplier characteristics of the model in response to a government expenditure shock.
2.6.1 Within and Out of Sample Dynamic Simulations
Root mean square percentage errors from within and out of sample dynamic simulations are given in Table 6 for each set of estimates. These results are also given in graphical form in Figure 2.
It is particularly noticeable from Figure 2 that in general the within sample root mean square percentage errors increase with the lengthening of the sample period. This should be qualified however by noting that the estimates for the longer sample periods have to predict more and more of the variable 1970s data. Thus the test may be biased in favour of the estimates for the shorter sample periods. In an attempt to account for this, although not fully, the various sets of estimates were simulated over a common within sample period, that is, 1966(3)–1971(3).[31]
| Variable | EST713 | EST724 | EST734 | EST744 | EST754 | EST764 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Within Sample (21 obs) | Out of Sample (24 obs) | Within Sample (26 obs) | Out of Sample (19 obs) | Within Sample (30 obs) | Out of Sample (15 obs) | Within Sample (34 obs) | Out of Sample (11 obs) | Within Sample (38 obs) | Out of Sample (7 Obs) | Within Sample (42 obs) | Out of Sample (3 Obs) | ||||||
| Expenditure | 2.0 | 13.0 | 3.5 | 24.9 | 2.0 | 4.6 | 5.1 | 5.3 | 2.7 | 1.4 | 9.0 | 1.3 | |||||
| Exports | 6.3 | 7.6 | 5.2 | 17.2 | 6.3 | 12.7 | 7.3 | 17.4 | 7.1 | 13.7 | 5.9 | 11.7 | |||||
| Imports | 5.5 | 10.8 | 7.3 | 37.0 | 4.0 | 24.5 | 9.4 | 8.4 | 7.0 | 4.5 | 16.7 | 5.8 | |||||
| Stocks | 1.5 | 12.6 | 2.5 | 21.7 | 1.5 | 8.9 | 6.0 | 5.7 | 5.7 | 3.9 | 5.0 | 3.9 | |||||
| Output | 2.8 | 7.0 | 3.2 | 15.1 | 2.5 | 5.0 | 3.5 | 11.3 | 2.7 | 4.1 | 7.2 | 1.3 | |||||
| Prices | 3.5 | 10.7 | 5.7 | 7.4 | 3.0 | 4.4 | 4.0 | 20.9 | 6.4 | 1.2 | 16.7 | 1.6 | |||||
| Wages | 3.8 | 7.8 | 5.2 | 6.7 | 3.0 | 7.4 | 3.5 | 19.6 | 6.0 | 1.5 | 17.5 | 0.3 | |||||
| Employment | 0.7 | 6.7 | 1.0 | 10.5 | 0.8 | 3.2 | 1.4 | 17.7 | 0.7 | 1.6 | 4.2 | 0.6 | |||||
| Capital Flows | 6.3 | 36.7 | 4.2 | 20.8 | 3.6 | 14.4 | 13.1 | 20.8 | 6.0 | 5.7 | 25.4 | 3.9 | |||||
| Reserves | 34.7 | 185.2 | 17.5 | 189.8 | 30.7 | 50.0 | 40.2 | 19.6 | 29.7 | 51.3 | 28.5 | 27.6 | |||||
| Bonds | 6.2 | 10.7 | 6.6 | 27.1 | 2.8 | 10.4 | 2.8 | 5.5 | 7.6 | 8.5 | 16.8 | 6.2 | |||||
| Domestic Credit | 8.9 | 30.5 | 2.0 | 20.6 | 3.3 | 3.8 | 5.3 | 6.2 | 6.1 | 5.8 | 17.1 | 3.1 | |||||
| Money | 4.5 | 19.8 | 1.3 | 16.7 | 5.1 | 7.7 | 8.5 | 7.9 | 6.6 | 2.2 | 15.8 | 1.3 | |||||
| Exchange Rate | – | – | 2.3 | 30.7 | 1.5 | 16.9 | 3.8 | 10.3 | 3.4 | 7.3 | 14.1 | 4.6 | |||||
| Variable | EST713 | E3T724 | EST754 | EST744 | EST754 | EST764 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Within Sample (21 obs) | Out of Sample (24 obs) | Within Sample (21 obs) | Out of Sample (19 obs) | Within Sample (21 obs) | Out of Sample (15 obs) | Within Sample (21 obs) | Out of Sample (11 obs) | Within Sample (21 obs) | Out of Sample (7 obs) | Within Sample (21 obs) | Out of Sample (3 obs) | ||||||
| Expenditure | 2.0 | 13.0 | 2.9 | 23.6 | 1.0 | 2.9 | 2.8 | 3.3 | 2.2 | 5.9 | 3.1 | 1.9 | |||||
| Exports | 6.3 | 7.6 | 5.4 | 21.4 | 6.7 | 12.9 | 6.9 | 13.8 | 6.5 | 13.1 | 6.7 | 11.7 | |||||
| Imports | 5.5 | 10.8 | 6.2 | 21.4 | 4.4 | 12.9 | 6.1 | 12.0 | 4.6 | 6.3 | 5.8 | 4.3 | |||||
| Stocks | 1.5 | 12.6 | 1.4 | 22.5 | 1.3 | 8.7 | 1.7 | 3.7 | 1.8 | 4.5 | 2.4 | 3.3 | |||||
| Output | 2.8 | 7.0 | 2.6 | 16.4 | 2.6 | 3.3 | 2.7 | 4.1 | 2.7 | 7.4 | 2.3 | 2.7 | |||||
| Prices | 3.5 | 10.7 | 3.9 | 15.7 | 2.1 | 11.2 | 3.8 | 11.8 | 7.0 | 13.4 | 9.4 | 5.1 | |||||
| Wages | 3.8 | 7.8 | 3.8 | 15.8 | 2.6 | 13.9 | 3.4 | 14.1 | 6.1 | 12.9 | 7.9 | 2.7 | |||||
| Employment | 0.7 | 6.7 | 1.0 | 12.6 | 0.9 | 2.5 | 0.5 | 1.8 | 0.5 | 3.8 | 0.4 | 1.0 | |||||
| Capital Flows | 6.3 | 36.7 | 3.9 | 11.2 | 4.1 | 33.0 | 11.9 | 39.5 | 6.4 | 61.1 | 10.3 | 50.2 | |||||
| Reserves | 34.7 | 185.2 | 16.9 | 71.3 | 33.0 | 136.4 | 40.7 | 155.9 | 30.8 | 246.2 | 38.1 | 192.9 | |||||
| Bonds | 6.2 | 10.7 | 3.1 | 36.8 | 2.3 | 9.8 | 2.3 | 8.5 | 3.5 | 5.4 | 2.6 | 9.9 | |||||
| Domestic Credit | 8.9 | 30.5 | 1.9 | 16.8 | 1.5 | 3.6 | 1.0 | 8.8 | 4.8 | 7.1 | 8.1 | 3.8 | |||||
| Money | 4.5 | 19.8 | 1.2 | 19.5 | 3.3 | 18.9 | 5.5 | 13.8 | 7.6 | 27.9 | 11.6 | 22.9 | |||||
| Exchange Rate | – | – | 2.5 | – | 0.7 | – | 3.1 | – | 2.7 | – | 4.0 | – | |||||
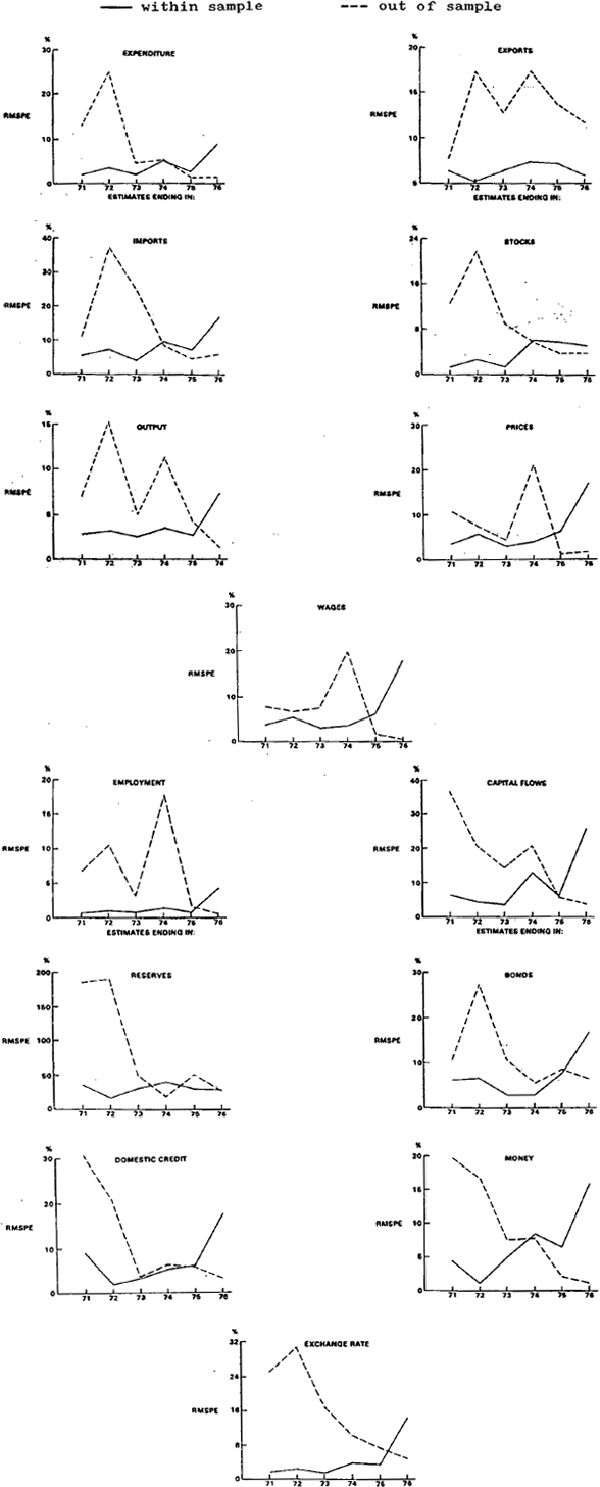
In general, similar trends in root mean square percentage errors, even if less pronounced, are evident. Thus it would appear that lengthening the sample period, in itself (that is with the same model structure) need not lead to a better explanation of the past.[32]
Figure 2 also shows that there are noticeable trends in out of sample ex post dynamic simulations. The procedure used to generate these results was to simulate the model out of sample exactly as it was estimated. This procedure may bias the results in favour of the longer period estimates as these models have the advantage of various dummy or synthetic variables which operate both within and out of sample. Again the model specifications are altered to give, in simulation, a structure similar to the estimates to 1971(3). That is, the exchange rate was exogenised, and the various dummy and synthetic variables which are not common to all models are set equal to zero.[33] Again these general trends in root mean square percentage errors persist except for the following closely related variables: capital flows, foreign reserves and money supply. The cause here lies with the setting of β24 to zero (the coefficient on the synthetic variable Qt in the capital flows equation).
2.6.2 Multiplier Characteristics
It is often difficult to distinguish between different models based on within or out of sample error properties. However one procedure which has been useful in distinguishing models is to subject the different models to a similar policy shock and examine the outcome.[34] The above subsection showed that within sample and out of sample simulation properties for the alternative estimates can be different. This subsection considers whether the one model estimated over different periods has similar multiplier characteristics.
The shock considered is a sustained 10 per cent increase in real government current expenditure. The period over which this experiment is conducted is the common simulation period 1966(3)–1971 (2).[35] Table 8 gives the output, prices and exchange rate multipliers for the various estimates.[36]
| Variable/ Quarters Elapsed |
Model | |||||
|---|---|---|---|---|---|---|
| EST713 | EST724 | EST734 | EST744 | EST754 | EST764 | |
| Output | ||||||
| 1 | 1.07 | 1.02 | 1.06 | .86 | .94 | .97 |
| 4 | 1.55 | 1.50 | 1.34 | 1.61 | 1.95 | 2.01 |
| 8 | 1.71 | 1.13 | 1.26 | 1.77 | 2.65 | 3.24 |
| 12 | 1.68 | .89 | 1.20 | 1.89 | 3.22 | 4.64 |
| 16 | 1.57 | .93 | 1.13 | 2.01 | 3.66 | 6.31 |
| 20 | 1.40 | .99 | 1.07 | 2.11 | 3.81 | 8.18 |
| Prices | ||||||
| 1 | .03 | .03 | .01 | .03 | .01 | .01 |
| 4 | .51 | .43 | .47 | .50 | .59 | .55 |
| 8 | 1.68 | 1.12 | 1.71 | 1.89 | 2.46 | 2.82 |
| 12 | 2.85 | 1.73 | 3.17 | 3.82 | 5.18 | 6.66 |
| 16 | 3.69 | 2.46 | 4.54 | 6.06 | 8.34 | 11.91 |
| 20 | 4.10 | 3.46 | 5.66 | 8.43 | 11.52 | 18.37 |
| Exchange Rate+ | ||||||
| 1 | – | −.01 | −.01 | −.01 | −.03 | −.03 |
| 4 | – | −.23 | −.06 | −.10 | −.52 | −.60 |
| 8 | – | −.33 | .03 | −.20 | −1.86 | −2.64 |
| 12 | – | .33 | .19 | −.20 | −3.31 | −5.87 |
| 16 | – | 1.57 | .43 | −.06 | −4.37 | −10.04 |
| 20 | – | 2.98 | .74 | .36 | −4.68 | −14.99 |
|
* The multiplier for variable X is approximated as 100 (log XS
– log XC), where X is the control solution and X the shock
solution. |
||||||
Several important features can be detected from this table. The first is that the multipliers vary substantially. The first three estimation periods have a traditionally shaped output multiplier, with an impact multiplier greater than one. But even amongst these three there are differences in the peak size, timing and rate of decline of the output multiplier.
For the three estimation periods ending in 1974, 1975 and 1976, output and price multipliers get increasingly large with time, in fact, implausibly large in some cases. Further, the longer the estimation period the greater the value of the multiplier.
Some understanding of the differences in these six sets of output and price multipliers can be obtained by considering the exchange rate response to the government expenditure shock. With the lengthening of the sample period the exchange rate revalues more and more. Thus for the estimates to 1972(4) the exchange rate revalues slightly at first in response to the improvement in the labour market etc. but then as domestic inflation takes off purchasing power parity takes over and the exchange rate devalues. For later period estimates the purchasing power parity term in the exchange rate becomes weak and hence the output increase leads to labour market improvement which causes further and further revaluations which are not offset by the worsening domestic inflation. The strong output effect is also a consequence of the revaluing exchange rate. This is because the revalued exchange rate creates monetary disequilibrium by lowering desired money balances; also less bonds are sold to the non-bank public leading to growth in actual money holding which further accentuates the excess monetary imbalances. Monetary disequilibrium than has a strong effect on consumption[37] and prices.
The behaviour of the exchange rate reaction function is somewhat surprising – and highly implausible – given the fact that the earliest model estimates have the least data on which to estimate a reaction function. If the exchange rate is exogenised in simulation then the multipliers move in the direction of the multiplier for the EST724 estimates. However, this is not the whole story. Because of the systems estimation procedure used it is difficult to isolate the causes of particular results. Nevertheless, the reasons for the changed responses of the EST754 model with respect to the model in Eberhardt et al and for the implausible responses in the EST744 and EST764 models appears to lie to a large extent with the behaviour of the labour market pressure (L/N) parameters that occur in various equations. These parameters can shift strongly in both numerical size and significance. As an example of the impact these parameters can make the model was re-estimated over the period to 1976(4) with the (L/N) parameters in the labour supply equation (σ8) and interest rate and exchange rate reaction functions (σ17 and σ18), constrained to their corresponding estimates from EST734. The output multiplier from this set of estimates changes substantially.
These results show that different multipliers can be obtained depending on the assumed behaviour of crucial parameters and of policy instruments. The implications here, for models that incorporate reaction functions, is that close attention needs to be paid to the estimation of reaction functions as small changes in the data set can give different simulation responses for the model. For models that do not include reaction functions for policy instruments, the results suggest that policy shocks should be conducted under a variety of assumptions about policy instruments.
Overall these results illustrate a more general point about model building. The procedure of updating a model's parameter estimates by successively adding observations and paying no attention (in an economic sense as distinct from a statistical sense) to the simulation properties of the model as a whole is highly dangerous. It is easy for a model to evolve longer run multiplier characteristics which most economists would regard as unacceptable. The general point is that building a satisfactory model involves attention to a whole set of criteria. Ignoring any one of these can lead to curious results, as it has in the above experiments. But there are some complex issues involved here, since rejection of apparently curious results can lead the model builder continually to impose the conventional wisdom on the model.
Footnotes
See Norton (ed.) (1977). [4]
Eberhardt et al (1978, p. 43). [5]
Some reasons for the implausible responses are considered below. [6]
See for example Porter's comments in Norton (ed.) (1977), pp275–281. [7]
Challen and Hagger (1979) suggest that certain estimation procedures in themselves may lead to parameter instability. There appears to be little or no evidence for this possibility from the RBA76 project. [8]
Implicit in estimating a model over a given period is the assumption that the model's specification is relevant for any subperiod and usually for some period into the future. [9]
This issue is not examined in this paper. [10]
As discussed below, under certain conditions it has been necessary to constrain particular parameters. [11]
The estimation technique is full information maximum likelihood. The RESIMUL programme developed by C.R. Wymer is used. See Wymer (1976). [12]
No two periods have mutually exclusive data. Whilst this would be an advantage, the estimation technique excludes this possibility because of the small sample problem. [13]
Strictly speaking these alterations ar'e not changes in the specification. Rather, variables involved have zero observations for these estimation periods. [14]
This results in the setting of the following parameters to zero:
1959(3)–1974(4) (EST744) : σ11
1959(3)–1973(4) (EST734) : σ11, σ3
1959(3)–1972(4) (EST734) : σ11, σ3, σ10,
σ24, σ20
1959(3)–197l(3) (EST713): σ11, σ3, σ13,
σ24
The dropping of parameters σ10 and σ11 does not change
the number of estimated parameters as both these coefficients are constrained in
estimation.
[15]
This involves the removal of the following parameters from the 1959(3)–1971(3) estimates: α18, σ20, σ21, σ22, σ23 and σ24. [16]
The implicit treatment of exchange rate expectations involves two components, one exogenous and operating only over the flexible exchange rate period, QE, and one endogenous operating over the whole of the estimation period, EPW/P. This results in the following parameters being excluded from the 1959(3)–1971(3) estimates: β5, β6, σ4, β13, β19, β20, β22, β23, β26 (previously constrained), and β27. [17]
These problems may indicate that some parameters are only well identified when data for the middle seventies are included. In addition, as all the estimation periods have the same starting period, these parameters estimates are likely still to be poorly determined over the full period. More accurate estimates might in this case be obtained by moving the starting point of the sample period. Because of small sample problems this is not done. The small sample problem may also be a factor in causing convergence problems with the shorter estimation periods discussed above. In principle it is impossible, at least at present, to determine the degrees of freedom for a complex simultaneous system (that is, one which includes nonlinear within and across equation restrictions on parameters). See Sargan (1975). [18]
Appendix C contains the results of the various tests conducted on RBA76 (T) in Section 2.4 when the base is the estimates to 1971(3) rather than the estimates to 1975(4). [19]
If P. and P2 are the two sets of parameter estimates then the variance of
(P1−P2) is given by
var(P1−P2) = var(P1) + var(P2) −
2cov(P1, P2).
As P1 and P2 have a large common sample period it would be
expected that cov(P1, P2) ≥ 0. Consequently the test presented
here is likely to bias the results in favour of acceptance of the null hypothesis of
equality between the two sets of parameters.
[20]
To facilitate comparisons across all models, parameters not estimated in the model to 1971(3) are excluded from the analysis except in two instances. For the estimates to 1971(3) it is assumed that α13 and α14 have the same standard errors in addition to the same parameter values as the estimates to 1973(4) at which values they are constrained. Similarly for α14 in the estimates to 1972(4). This leaves 53 parameters for comparison. [21]
That is H0: P1 = 
H1 : P1 ≠ 
where  is the predetermined parameter set, P1 the
alternative parameter set, and the normalised test statistic is (P1 −
is the predetermined parameter set, P1 the
alternative parameter set, and the normalised test statistic is (P1 −
 )/
)/ .
[22]
.
[22]
At the 5% level of significance. [23]
It should be noted that with a full information maximum likelihood estimation procedure the lengthening of the sample period by four observations means that the system of equations has to explain not just four addition observations but four additional observations on all the endogenous variables. [24]
It will be remembered that it was the estimates to 1972(4) that failed to converge absolutely. [25]
That is H0: P1 = P2
H1: P1 ≠ P2
where P2 is the EST754
parameter set, P1 is the alternative parameter set, and the normalised test
statistic is (P1−P2)/ . Also see
footnote 1 page 9.
[26]
. Also see
footnote 1 page 9.
[26]
A significant change of sign is said to have occurred if a parameter changes from being significantly different from zero to being of the opposite sign and significantly different from zero at the 5% level of significance. [27]
Such a procedure is recommended by Zellner (1977, p. 48) and can also be linked with the issues emphasised by Lucas (1976). [28]
These particular parameters are chosen because monetary disequilibrium has been a central and distinguishing feature of the RBA76 modelling project. For a discussion of the role of monetary disequilibrium see Jonson and Taylor (1978). [29]
Figure 1 plots the parameter estimates and the parameter's confidence interval at the 5% level of significance. [30]
See within sample columns of Table 7. [31]
It may however, be important in out of sample ex ante simulations. [32]
See out of sample columns in Table 7. [33]
See for example Christ (1975) and Helliwell et al (1979). [34]
For estimation and simulation RBA76(T) is linearised, hence the simulation period is not important. [35]
The table shows impact multipliers and multipliers calculated at the end of each four quarters. [36]
This is the case even though the monetary disequilibrium parameter in the expenditure equation (γ1) gets less negative with the lengthening of the sample period. [37]