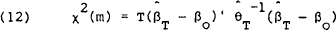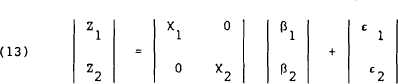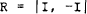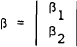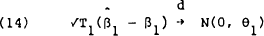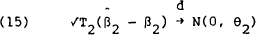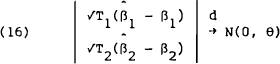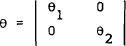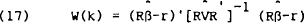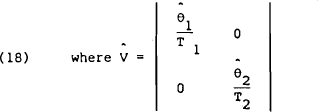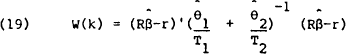RDP 8603: Risk Premia, Market Efficiency and the Exchange Rate: Some Evidence Since the Float 4. Data and Results
May 1986
- Download the Paper 662KB
(a) Full Sample Tests
Data on US$/$A spot and forward rates were obtained from the Daily Exchange Rate release of the Commonwealth Bank of Australia.[7] Tests were conducted across a range of maturities. In particular, tests of the efficiency of the 15-day, 30-day and 90-day forward markets were conducted. The results of estimating equations (4) through (8) for each of these markets are reported in Tables 1 through 5. In equations (4) through (7) we are interested in testing the joint null hypothesis that all coefficients in each equation are zero while in equation (8) we are interested in testing the hypothesis that α = 0 and β = 1. These joint hypotheses are tested via the Χ2 (m) statistic, which has the form
This statistic has a Χ2 distribution with m degrees of freedom, where m is the number of restrictions.
The results of estimating equation (4), given in Table 1, show that the null hypothesis, that
the mean of the forecast error is zero, cannot be rejected in any of the markets. Furthermore,
from Table 2, there is little evidence of serial correlation in the forecast errors of the
15-day and 90-day markets. Although an individual parameter, 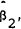 in the
15-day market is significantly different from zero, the Χ2 statistic indicates
that the joint null hypothesis α = β = 0 cannot be
rejected. However, in the 30-day market there is evidence of serially correlated forecast
errors; the Χ2 statistic is highly significant. The sequence of forecast errors
in the 30-day market are not uncorrelated suggesting that this market is not speculatively
efficient.
in the
15-day market is significantly different from zero, the Χ2 statistic indicates
that the joint null hypothesis α = β = 0 cannot be
rejected. However, in the 30-day market there is evidence of serially correlated forecast
errors; the Χ2 statistic is highly significant. The sequence of forecast errors
in the 30-day market are not uncorrelated suggesting that this market is not speculatively
efficient.
| Maturity | T | 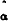 |
R2 | Χ2(m) |
|---|---|---|---|---|
| 15 day | 111 |
−0.003 (0.004) |
0.0 |
– |
| 30 day | 109 |
−0.006 (0.008) |
0.0 |
– |
| 90 day | 102 |
−0.026 (0.026) |
0.0 |
– |
Standard errors are in brackets. |
||||
| Maturity | T | 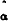 |
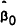 |
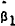 |
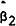 |
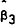 |
R2 | Χ2(5) |
|---|---|---|---|---|---|---|---|---|
| 15 day | 107 |
−0.004 (0.004) |
0.248 (0.136) |
−0.261* (0.124) |
0.032 (0.123) |
−0.032 (0.134) |
0.04 |
6.81 |
| 30 Day | 103 |
−0.006 (0.009) |
0.107 (0.164) |
−0.318** (0.102) |
0.157 (0.103) |
0.185 (0.165) |
0.06 |
26.77** |
| 90 Day | 86 |
−0.040 (0.031) |
0.199 (0.333) |
−0.001 (0.126) |
−0.022 (0.109) |
−0.496 (0.305) |
0.15 |
4.20 |
| See footnotes Table 1 | ||||||||
These two tests are weak form tests of efficiency. Semi-strong form tests of efficiency are provided by estimating equations (6) and (7). The results of these estimations are reported in Table 3 and Table 4. In each of the markets it is found that neither lags of the forward premium nor lags of the spot holding period yield are significant explanators of the forecast error. Although some individual parameter estimates are significantly different from zero, each Χ2 statistic is insignificant. Thus, the respective joint null hypotheses α = γ = 0 and α = δ = 0 cannot be rejected.
| Maturity | T | 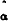 |
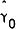 |
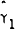 |
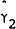 |
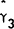 |
R2 | Χ2(5) |
|---|---|---|---|---|---|---|---|---|
| 15 day | 108 |
−0.009 (0.006) |
−3.083 (6.710) |
−6.168 (6.740) |
1.126 (4.650) |
5.053 (4.640) |
0.04 |
3.27 |
| 30 Day | 106 |
−0.017 (0.010) |
5.615 (4.400) |
6.763* (3.040) |
−3.668 (2.950) |
−5.862 (4.180) |
0.09 |
7.81 |
| 90 Day | 99 |
−0.050 (0.030) |
0.017 (5.780) |
−0.800** (0.200) |
3.991 (2.710) |
−5.987 (5.260) |
0.10 |
3.02 |
See footnotes Table 1 |
||||||||
| Maturity | T | 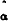 |
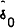 |
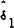 |
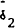 |
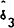 |
R2 | Χ2(5) |
|---|---|---|---|---|---|---|---|---|
| 15 day | 108 |
−0.003 (0.004) |
0.272 (0.148) |
−0.345* (0.155) |
0.219 (0.150) |
−0.098 (0.143) |
0.04 |
6.52 |
| 30 Day | 102 |
−0.006 (0.009) |
0.141 (0.205) |
−0.272 (0.167) |
−0.065 (0.169) |
0.377 (0.207) |
0.07 |
6.25 |
| 90 Day | 86 |
−0.045 (0.031) |
0.181 (0.385) |
−0.197 (0.244) |
0.158 (0.231) |
−0.542 (0.363) |
0.20 |
4.73 |
| See footnotes Table 1 | ||||||||
Finally, the results in Table 5 show that the forward rate is an unbiased predictor of future spot rates in each market. That is, the joint null hypothesis α = 0, β = 1 cannot be rejected.
| Maturity | T | 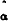 |
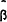 |
R2 | Χ2(2) |
|---|---|---|---|---|---|
| 15 day | 111 |
−0.013 (0.009) |
0.962** (0.033) |
0.95 |
1.98 |
| 30 day | 109 |
−0.027 (0.017) |
0.914** (0.060) |
0.90 |
2.60 |
| 90 Day | 102 |
−0.089 (0.046) |
0.733** (0.170) |
0.67 |
3.84 |
See footnotes Tables 1 |
|||||
These results suggest that, for the post float period as a whole, the joint hypothesis that agents are risk neutral and markets are efficient cannot be rejected in the 15-day and 90-day forward markets. However, this joint hypothesis can be rejected in the 30-day forward market where lagged forecast errors help predict the future spot rate. Because of the joint nature of these tests it is impossible to determine whether rejection in the 30-day market is due to market inefficiency or to risk aversion.
The major event experienced in the foreign exchange market since the float was the large depreciation of the Australian dollar which commenced in February 1985. Although this paper cannot explain whether this depreciation was a consequence of altered economic fundamentals or rational price bubbles, it can test to see if behaviour in the market has altered since its occurrence. The following sub-section constructs and implements a test of parameter instability which can be used in conjunction with the Hansen-Hodrick procedure.
(b) A Test of Parameter Stability[8]
As previously mentioned, because of the presence of serial correlation, estimation has proceeded by first obtaining consistent OLS parameter estimates and then estimating a consistent asymptotic covariance matrix. This procedure renders “traditional” tests of stability inappropriate. For instance, Cusum and Cusum of Squares tests (see Brown, Durban and Evans (1975) and Harvey (1983)) are not appropriate when there are serially correlated errors. Furthermore, the residual sum of squares produced by the OLS estimates are not appropriate for the construction of chow tests. To overcome this a Wald test is constructed which makes use of the consistent estimates of the asymptotic covariance matrices.
Consider the linear model
| zi | = dependent variable in period i |
| Χi | = vector of independent variables in period i |
| βi | = parameter vector in period i |
| εi | = stochastic residual in period i |
We are interested in testing whether the parameters are equal in both periods. The null hypothesis Ho: β1 = β2, can be expressed as
Rβ = r = 0
where R is a (k×2k) matrix of the form
and β is a (2k×1) vector of parameters of the form
and k is the number of parameters.
From equation (10) it follows that
and
which can be expressed as
where
and θ1 and θ2 are the asymptotic covariance matrices for periods 1 and 2.
A test statistic, W(k), for the linear restriction Rβ=r is given by
Substituting (18) into (17) gives
The results of these stability tests are reported in Tables 6 through 10. In each test the sample is divided into two periods, 13 December 1983 – 5 February 1985 and 12 February 1985 – 28 January 1986.[9]
| Period 1 | Period 2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Maturity | T1 | 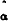 |
R2 | Χ2(2) | T2 | 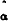 |
R2 | Χ2(2) | W(2) |
| 15 Day | 61 |
−0.007 (0.005) |
0.0 |
– |
50 |
0.001 (0.046) |
0.0 |
– |
0.80 |
| 30 Day | 61 |
−0.016 (0.011) |
0.0 |
– |
48 |
0.007 (0.010) |
0.0 |
– |
2.29 |
| 90 Day | 61 |
−0.057 (0.031) |
0.0 |
– |
41 |
0.019 (0.010) |
0.0 |
– |
5.55 |
See footnotes Table 1 |
|||||||||
| Period 1 | Period 2 | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Maturity | T1 | 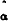 |
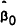 |
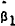 |
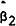 |
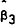 |
R2 | Χ2(5) | T2 | 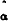 |
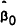 |
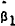 |
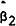 |
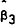 |
R2 | Χ2(5) | W(5) |
| 15 Day | 57 |
−0.006 (0.005) |
0.668* (0.261) | −0.470 (0.270) | 0.012 (0.255) |
0.097 (0.244) |
0.12 |
9.63 |
50 |
0.0 (0.007) |
0.136 (0.165) |
−0.205 (0.164) |
0.054 (0.165) |
−0.077 (0.167) |
0.03 |
2.04 |
4.16 |
| 30 Day | 55 |
−0.018 (0.011) |
0.351 (0.354) |
−0.279 (0.279) |
−0.129 (0.264) |
0.195 (0.358) |
0.02 |
5.16 |
48 |
0.009 (0.009) |
0.061 (0.154) |
−0.310* (0.138) |
0.205 (0.141) |
0.225 (0.158) |
0.17 |
9.67 |
5.45 |
| 90 Day | 45 |
−0.102** (0.026) |
0.002 (0.592) |
−0.532* (0.263) |
0.154 (0.257) |
−0.795 (0.515) |
0.42 |
20.17** |
41 |
0.015 (0.014) |
0.110 (0.374) |
0.115 (0.501) |
−0.003 (0.492) |
−0.312 (0.372) |
0.15 |
4.16 |
17.45* |
See footnotes Table 1 |
|||||||||||||||||
| Period 1 | Period 2 | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Maturity | T1 | 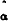 |
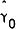 |
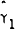 |
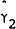 |
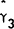 |
R2 | Χ2(5) | T2 | 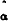 |
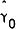 |
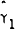 |
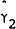 |
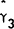 |
R2 | Χ2(5) | W(5) |
| 15 Day | 58 |
−0.007 (0.005) |
6.383 (11.609) |
7.235 (11.499) |
−5.560 (6.612) |
5.142 (5.925) |
0.16 |
9.65 |
50 |
−.0441* (0.018) |
−1.812 (9.415) |
−9.314 (9.032) |
−4.454 (9.106) |
−0.799 (9.281) |
0.19 |
7.39 |
11.90* |
| 30 Day | 58 |
−0.014 (0.008) |
−4.207 (6.321) |
−2.272 (2.784) |
−1.948 (4.811) |
−5.641 (5.034) |
0.40 |
17.67** |
48 |
−0.069** (0.023) |
5.500 (5.310) |
7.470* (3.303) |
2.499 (3.350) |
−3.177 (4.996) |
0.33 |
14.84* |
23.27** |
| 90 Day | 58 |
−0.033 (0.021) |
9.596 (5.349) |
2.442 (3.381) |
1.167 (3.714) |
0.645 (3.884) |
0.65 |
31.36** |
41 |
−0.096 (0.076) |
−0.141 (3.328) |
−8.318** (2.708) |
−0.921 (2.383) |
2.635 (4.034) |
0.24 |
110.79** |
35.07** |
See footnotes Table 1 |
|||||||||||||||||
| Period 1 | Period 2 | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Maturity | T1 | 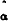 |
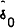 |
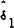 |
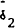 |
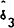 |
R2 | Χ2(5) | T2 | 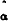 |
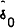 |
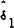 |
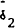 |
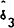 |
R2 | Χ2(5) | W(5) |
| 15 Day | 56 |
−0.006 (0.005) |
0.625** (0.261) |
−0.391 (0.289) |
0.162 (0.256) |
0.071 (0.235) |
0.11 |
8.84 |
49 |
0.000 (0.007) |
0.171 (0.182) |
−0.328 (0.203) |
0.229 (0.204) |
−0.147 (0.184) |
0.04 |
2.68 |
4.26 |
| 30 Day | 53 |
−0.018 (0.011) |
0.430 (0.380) |
−0.442 (0.327) |
−0.054 (0.324) |
0.322 (0.390) |
0.04 |
6.40 |
48 |
−0.010 (0.009) |
0.058 (0.195) |
−0.148 (0.195) |
−0.159 (0.202) |
0.476* (0.202) |
0.20 |
7.56 |
6.26 |
| 90 Day | 45 |
−0.101** (0.025) | 0.041 (0.484) |
−0.422 (0.281) |
0.088 (0.240) |
−0.794 (0.449) |
0.45 |
22.10** |
41 |
0.013 (0.011) |
0.081 (0.264) |
0.019 (0.289) |
0.100 (0.272) |
−0.317 (0.253) |
0.13 |
7.67 |
20.54* |
See footnotes Table 1 |
|||||||||||||||||
| Period 1 | Period 2 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Maturity | T1 | 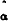 |
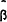 |
R2 | Χ2(2) | T2 | 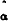 |
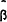 |
R2 | Χ2(2) | W(2) |
| 15 Day | 61 |
0.008 (0.014) |
1.111** (0.093) |
0.83 |
3.29 |
49 |
−0.259** (0.052) |
0.310* (0.139) |
0.15 |
24.79** |
24.75** |
| 30 Day | 61 |
0.008 (0.029) |
1.170** (0.199) |
0.70 |
2.94 |
48 |
−0.350** (0.076) |
0.065 (0.199) |
0.00 |
22.60** |
19.33** |
| 90 Day | 61 |
−0.001 (0.077) |
1.409** (0.519) |
0.48 |
4.92 |
41 |
−0.436** (0.126) |
−0.168 (0.323) |
0.07 |
15.07* |
8.70* |
See footnotes Table 1 |
|||||||||||
The results reported in Table 6 suggest that the mean of the forecast errors are insignificantly different from zero in both periods.
Tables 7 and 9 show that for the 15-day and 30-day markets the null hypothesis of speculative efficiency cannot be rejected in either period. However, in the 90-day market this null hypothesis can be rejected in Period 1 but not Period 2. Furthermore, there is evidence of parameter instability in the equations estimated for the 90-day market. The latter appears to be the result of changes to the constant terra. The last two rows of Table 11 report the results of testing the stability and significance of the constant term in both equations. In both cases the constant term is found to be unstable. The null hypothesis that α = 0 is rejected in Period 1 but not in Period 2 in both equations.
| Χ2(m) | ||||||||
|---|---|---|---|---|---|---|---|---|
| Maturity | Regressions | Null Hypothesis | m=k | Period 1 | Period 2 | Null Hypothesis | W(k) | |
| 30 Day | εt+n = α + γ(L)Pt,n + νt | α = γ1 = 0 | 2 | 4.57 | 22.82** | α1 = α2, γ11 = γ12a | 7.74* | |
| γ1=0 | 1 | 0.53 | 58.84** | γ11 = γ12 | 6.20* | |||
| α = 0 | 1 | 3.70 | 118.77** | α1 = α2 | 8.72* | |||
| 90 Day | εt+n = α + γ(L)Pt,n + νt | α = γ1 = 0 | 2 | 5.40 | 218.5** | α1 = α2, γ11 = γ12 | 10.60* | |
| γ1 = 0 | 1 | 1.26 | 142.3** | γ11 = γ12 | 16.50* | |||
| α = 0 | 1 | 3.03 | 113.6** | α1 = α2 | 1.95 | |||
| εt+n = α + β(L)εt + νt | α = 0 | 1 | 24.22** | 1.49 | α1 = α2 | 22.82** | ||
| εt+n = α + δ(L)Yt,n + νt | α = 0 | 1 | 24.76** | 2.13 | α1 = α2 | 25.08** | ||
See footnotes Table 1 |
||||||||
More striking results are to be found in Tables 8 and 10. First, consider Table 10. In all markets, the parameters are found to be significantly different in each period. In particular, the results show that while the forward rate was an unbiased predictor of future spot rates in Period 1 this was not the case in the subsequent period. On the basis of these results, the speculatively efficiency hypothesis can be rejected for all three markets in Period 2.
A similar result is obtained in Table 8.[10]
In the 15-day market there is evidence of instability. However, the speculative efficiency
hypothesis cannot be rejected in either period. In the 30-day and 90-day markets, however, the
null hypothesis of speculative efficiency is rejected in both periods. Additionally,
there is evidence of a structural break in these equations. Closer inspection of Table 8 reveals
that, in both the 30-day and the 90-day markets, the parameter 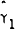 becomes highly significant in Period 2 and in the 30-day market the constant term also becomes
significant in this period. One interpretation of this result is that the first lag of the
forward premium could be used to reduce the observed forecast error in the latter but not the
former period. That is, the market failed to use all available information when setting the
forward price in the post depreciation period. To examine this hypothesis the stability and
significance of α and γ1 are tested, both individually and, where
appropriate, Jointly. The relevant Χ2 and Wald tests are reported in the first
six rows of Table 11.
becomes highly significant in Period 2 and in the 30-day market the constant term also becomes
significant in this period. One interpretation of this result is that the first lag of the
forward premium could be used to reduce the observed forecast error in the latter but not the
former period. That is, the market failed to use all available information when setting the
forward price in the post depreciation period. To examine this hypothesis the stability and
significance of α and γ1 are tested, both individually and, where
appropriate, Jointly. The relevant Χ2 and Wald tests are reported in the first
six rows of Table 11.
The results in Table 11 show that both singularly and Jointly the coefficients α and γ1 in the equation relating to the 30-day market become significantly different from zero in period 2 and that they are unstable over time. For the 90-day market each restriction Is rejected in the second period and the parameter γ1 is found to be unstable. These results are consistent with the hypothesis that the first lag of the forward premium could be used to reduce the observed forecast errors in the latter but not the former period.
These results suggest that after the February 1985 depreciation there has been a significant change in some of the relationships in the forward market. Both weak form (Table 10) and serai-strong form (Table 8) tests of the speculative efficiency hypothesis are rejected for the period after February 1985 but are not rejected for the period before this time. In the 90-day market there is also evidence of speculative inefficiency in the earlier period.
Footnotes
For a more detailed description of the construction of the data see the Appendix. [7]
I am grateful to Rob Trevor for suggesting the test statistic used in this section. [8]
The observation for 5 February 1985 was chosen to split the sample because it represents the start of the large depreciation. In the period from December 1983 to the end of January 1985 the $A depreciated by about 12 per cent against the US$, or approximately 0.2 per cent per week. From 5 February 1985 – 12 February the $A depreciated by about 4 per cent against the US$, while for the month of February as a whole the depreciation was around 17 per cent. [9]
At first it appears that the Χ2 and t-statistics in the equations relating to the 30-day and 90-day markets are inconsistent. The Χ2statistics, for instance, reject the joint hypothesis that all the parameters are equal to zero whereas the t-statistics suggest that, individually, each of the parameters are zero. The relatively high R2's in these equations suggest that the equations, as a whole, explain a significant proportion of the forecast error. This is consistent with the significant Χ2 tests. It is likely, therefore, that the insignificance of individual parameters is caused by multi-collinearity. [10]