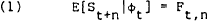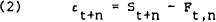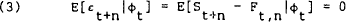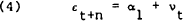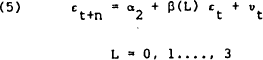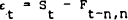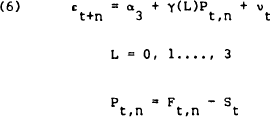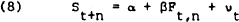RDP 8603: Risk Premia, Market Efficiency and the Exchange Rate: Some Evidence Since the Float 2. Joint Tests of Risk Neutrality and Market Efficiency
May 1986
- Download the Paper 662KB
In an efficient market, agents cannot derive abnormal returns by systematically exploiting available information. In the forward market, for instance, if some agents are risk neutral and the market is informationally efficient, the forward price will equal the expected spot price. Given the assumptions of risk neutrality and market efficiency, any systematic deviation between these two prices would indicate unexploited profit opportunities in the forward market. The assumption of risk neutrality ensures this equality holds. This is because the forward price embodies both expectations of future spot prices and a risk premium reflecting the riskiness of the forward contract. Risk neutrality ensures that this risk premium is zero.
If the forward market is informationally efficient and if agents are risk neutral then the forward rate will equal the expected future spot rate (or the rational expectation of the future spot rate), thus
| where | Ft,n | = forward rate contracted at period t for payment at period t+n |
| St+n | = spot rate in period t+n | |
| Φt | = information set available to agents at period t | |
| E[.|Φt] | = mathematical expectation conditional on Φ(t) |
Forward rates and spot rates are expressed as natural logs (hence ignoring Jensen's inequality).
The conditional forecast error, εt+n, can be written as
Given market efficiency and risk neutrality, as defined in (1), the expected forecast error is
If the joint hypothesis of speculative efficiency is valid, then the expected value of the conditional forecast error is zero. If εt+n has a zero mean then the constant term, α1, in equation (4) should be insignificantly different from zero
Furthermore, εt+n should be uncorrelated with variables in the information Φt. Any correlation between variables in Φt and εt+n would indicate that Ft,n is not an optimal predictor of St+n. Thus, by positing variables that may appear in Φt, several testable implications of (3) can be developed.
Although the choice of variables that may be elements of Φt is partly arbitrary, it is assumed that Φt contains observable lagged values of
- the expectation error, εt+n,
- the spot holding period yield, Yt,n = St − St−n,
- the forward premium, Pt,n = Ft,n −S t.
Geweke and Feige (1979), Hansen and Hodrick (1980) and Hsieh (1982) have also chosen to use various combinations of the above variables as elements of Φ. The rationale for this choice of information variables is as follows. If forward rates are rational expectations of future spot rates then the observed forecast errors should be uncorrelated with future forecast errors. Hence, lagged forecast errors should not provide additional information about future forecast errors. The spot holding period yield represents the return to pure spot exchange rate speculation (i.e., abstracting from interest received on any financial assets held over the n periods). Any information which this yield provides about future spot prices should be reflected in the forward price. Similarly, any information which the forward premium (which, given covered interest rate parity, is a proxy for interest differentials) provides about future spot prices should be reflected in the forward price.
Thus we are provided with several tests of efficiency and risk neutrality. The following regressions[4] will reveal whether εt+n is correlated with elements of Φt
where
Equations (4) and (5) in combination provide a test of whether the series εt+n is a fair game.[5] If the sequence of εt+n is a fair game then α1 = 0 and α2 = βi = 0 for all i. Furthermore, if εt+n is uncorrelated with Φt then the estimated coefficients in (6) and (7) should satisfy the condition α3 = γi = 0 and α4 = δi = 0, for all i, respectively.
Finally, if the market is efficient and agents are risk neutral then the forward rate should be an unbiased predictor of future spot rates. A simple test of unbiasedness is given in (8)
Unbiasedness will be satisfied if α = 0 and β = 1.
If the restrictions associated with any of these equations are not supported by the data then the joint null hypothesis of speculative efficiency can be rejected.
Footnotes
The choice of lag length is arbitrary. However, for the sake of parsimony I shall restrict the analysis to four lags. This is also in keeping with previous studies such as Hansen and Hodrick (1980). [4]
The sequence εt+n is a fair game if E[εt+n|Φt] = 0 and εt+n is not serially correlated. If this condition holds then the expected return to speculation will equal the actual return. [5]