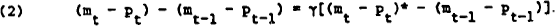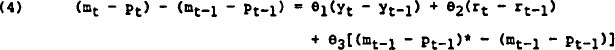RDP 8701: The Australian Demand Function for Money: Another Look at Stability 2. The Models

Glenn Stevens, Susan Thorp and John Anderson

January 1987

The models of interest here are fairly conventional. In common with much of the overseas literature, they are developed in something like the following way.

Let the desired stock of money be denoted by

where yt is real income, rt is the rate of interest, all variables are in logs,[5] and the expected signs on parameters are β1 > 0, β2 < 0.

Then let the actual stock of real balances held adjust towards the desired stock according to

Straight forward substitution of (1) into (2) gives (3), the so-called “Koyck-lag” specification:

where αi = γβi for i = 0, 1, 2

and α3 = 1−γ.

The lagged-adjustment hypothesis is a convenient justification for using equation (3) as an estimating equation, especially since a specification such as (3) normally fits the data much more closely than (1). Two studies considered here – Sharpe and Volker (1977) and Porter (1979) – used models of this type.

Yet equation (3), or at least the empirical versions of it, has not been without its problems in the literature, such as the tendency for the estimated value of γ to approach zero, implying very long lags in adjustment process. Results such as Inline Equation = 0.9 (which are not uncommon), imply in a quarterly model that only half of the adjustment towards the desired stock of money has taken place after a year and a half.

An alternative approach recognises the fact that the Koyck specification constrains the speed of adjustment of money demand to changes in different variables on the right hand side to be at the same rate, without actually testing whether this restriction is supported by the data.

A response to this is to propose a more general adjustment process, like that in (4):

This approach – Hendry and Mizon's (1978) “error-correction mechanism” – was adopted for M1 with some success by Pagan and Volker (1980, 1981), with the specification being narrowed down to something like (3), but with a lagged interest rate term added. Of course, this is only one of any number of more general lag specifications which might be employed. Sharpe and Volker (1977) also investigated distributed lag formulations, using the Almon technique.

Table 1
Sharpe and Volker's Equation
  Constant S1 S2 S3 ln(GDP/P) lnR2 ln(M3/P)−1 Inline Equation Inline Equation h
SV-1 Original
52(2)–72(3)
ln(M3/P)		 0.427
(2.60)		 0.022
(2.37)		 −0.004
(−0.37)		 0.002
(0.40)		 0.225
(5.13)		 −0.056
(−3.12)		 0.756
(13.95)		 0.998
 		 0.57
 		 1.53
 
SV-2 Revised
52(3)–72(3)
ln(M3/P)		 0.205
(2.239)		 −0.027
(−7.140)		 −0.0501
(−13.417)		 −0.019
(−5.440)		 0.1787
(4.009)		 −0.072
(−4.833)		 0.8187
(15.410)		 0.995
 		 0.336
 		 0.203
 
SV-3 Updated
52(3)–86(1)
ln(M3/P)		 0.332
(3.257)		 −0.019
(−5.133)		 −0.045
(−12.35)		 −0.012
(−3.421)		 0.219
(6.083)		 −0.048
(−5.446)		 0.76
(16.954)		 0.996
 		 0.317
 		 1.002
 
(a) Sharpe and Volker corrected for first order serial correlation using the Cochrane-Orcutt iterative procedure and the ρ reported. Equations SV-2 and SV-3 were adjusted using a two-step Yule-Walker procedure.

GDP = gross domestic product, seasonally adjusted in current prices
R2 = Yield on two-year rebate Commonwealth Government bonds for equations SV-1 & SV-2. The yield on two-year non-rebate bonds was used from 69(3) for equation SV-3.
P = Consumer Price Index, with base year 1980–81.
Si = seasonal dummy, equal to 1 in quarter 1 and zero otherwise.

Table 2
Porter's Equation
  Constant S1 S2 S3 ln(GDP) lnR2 ln(M3/P)-1 Inline Equation h
PO–1 Original
66(3)–79(2)
ln(M3/P)		 1.46
(2.17)		 *
 		 *
 		 *
 		 0.204
(3.70)		 −0.073
(−4.40)		 0.818
(10.38)		 0.976
 		 0.324
 
PO–2 Revised
66(3)–79(2)
ln(M3/P)		 0.636
(1.297)		 0.004
(0.315)		 −0.028
(−2.215)		 −0.003
(−0.32)		 0.218
(3.95)		 −0.06
(−3.60)		 0.747
(9.109)		 0.959
 		 −0.273
 
PO–3 Updated
69(3)–86(1)
ln(M3/P)		 −0.731
(−1.634)		 0.002
(0.188)		 −0.026
(−2.518)		 −0.001
(−0.143)		 0.205
(4.234)		 −0.057
(−3.94)		 0.806
(15.352)		 0.958
 		 0.276
 

GDP = GDP in current prices.
P = implicit deflator for GDP, base year 1974/75.
R2 = yield on two-year non-rebate Commonwealth Government bonds.
* Estimated values for seasonal dummies were not reported by Porter.

Table 3
Freeland's Equation
  Constant lnGDP lnRGS−1 lnRSSA−1 lnRFD−1 ln(M3/P)−1 Inline Equation h
FR–1 Original
67(3)–83(2)
ln(M3/P)		 1.0294
(2.85)		 0.2292
(4.95)		 −0.1101
(−6.08)		 0.0242
(2.48)		 0.0648
(2.91)		 0.6934
(11.46)		 0.97
 		 0.37
 
FR–2 Revised
67(3)–83(2)
ln(M3/P)		 1.07
(2.92)		 0.229
(4.997)		 −0.114
(−6.115)		 0.025
(2.512)		 0.0665
(2.892)		 0.6899
(11.545)		 0.977
 		 −0.108
 
FR–3 Updated
67(3)–85(1)
ln(M3/P)		 0.964
(2.951)		 0.226
(5.114)		 −0.113
(−6.318)		 0.028
(3.454)		 0.063
(2.861)		 0.703
(12.317)		 0.982
 		 0.105
 

GDP = GDP in current prices.
P = implicit deflator for GDP, base year 1979/80.
RGS = yield on 2 year government securities.
RSSA = interest rate on statement savings accounts
RFD = interest rate on trading bank fixed deposits

Table 4
Pagan and Volker's Equation
  Constant S1 S2 S3 lnGDP/P ln(M1/P)-1 RBILL RBILL-1 Inline Equation h
PV–1 Original
67(4)–78(2)
ln(M1/P)		 0.42
(1.01)		 0.008
(1.16)		 −0.039
(−5.00)		 0.44
(6.10)		 0.113
(4.96)		 0.845
(18.27)		 −0.003
(−2.22)		 −0.006
(−4.37)		 0.94
 		 0.894
 
PV–2 Revised
67(4)–78(2)
ln(M1/P)		 0.379
(0.759)		 −0.013
(−1.48)		 −0.067
(−6.55)		 −0.048
(−5.24)		 0.127
(4.27)		 0.836
(14.74)		 −0.003
(−1.71)		 −0.007
(−3.54)		 0.916
 		 −0.445
 
PV–3 Updated
67(4)–85(4)
ln(M1/P)		 0.247
(0.511)		 −0.0159
(−2.028)		 −0.0682
(−7.87)		 −0.094
(−5.81)		 0.126
(5.31)		 0.848
(16.84)		 −0.002
(−0.60)		 −0.006
(−3.38)		 0.883
 		 −0.34
 

GDP = GDP in current prices.
P = implicit deflator for GDP, base year 1974/75.
RBILL = yield on 90-day bank-accepted bills of exchange.
Si = seasonal dummy, equal to 1 in quarter 1, zero elsewhere.

Attempts to reproduce the results of the studies in question met with varying degrees of success. Equation SV-1 in Table 1 is the equation originally reported in Sharpe and Volker (1977). SV-2 represents our best efforts to reproduce the original parameter estimates, using (as far as possible) the same data. SV-3 is the result of estimation over a revised and extended data set. Analogous notation is used in Tables 2, 3 and 4 for the Porter, Freeland and Pagan and Volker studies.

In most cases, data revisions presented difficulties. This was especially so in the case of equation SV-1 from Sharpe and Volker (1977). where despite considerable effort, a number of parameters in our estimations remained noticeably different to those reported by the original authors. In particular, the first-order autocorrelation parameter reported in the original paper proved quite elusive. Equation SV-2 reported in Table 1 utilises a two-step Yule-Walker procedure available in SAS for correcting for first-order serial correlation. Although Sharpe and Volker used an iterative Cochrane-Orcutt technique, we have reported (and used) equation SV-2 because the slope parameters were closer to those in the original paper than were those in our attempts to reproduce the Cochrane-Orcutt specification. (The biggest differences occur in the coefficients on the seasonal dummies.) Our specification is further defensible because it is not apparently troubled by auto-correlation after the Yule-Walker procedure is applied, whereas the equation reported by Sharpe and Volker is suspect in this regard, even after using the Cochrane-Orcutt procedure.[6]

In fact the latter problem was behind Sharpe and Volker's decision not to use this equation for stability tests, since auto-correlation would upset the tests based on cumulative sums of recursive residuals. They go on to estimate alternative models, with the preferred ones being distrlbuted-lag formulations.

These equations, shown as equations SV-4 and SV-6 in Tables A.1 and A.2 in the Appendix, proved no easier to re-produce. For computational reasons, it was not possible to apply stability tests to them. The results reported in Section 4 below relate to equations SV-2 and SV-3.

Porter (1979) uses a similar specification to equation SV-1, although over a shorter and later sample period. The original results and our updates are shown in Table 2. The estimation period was originally 1966(3)–1979(2), and over this period our regressions provided parameter estimates fairly close to those in the the original paper. When updating the equation to 1986(1), consistent data could be used only back to 1969(3), due to the change in the base period for quarterly national accounts data introduced in 1982 – hence the different starting date for equation PO-2. The altered sample period has the effect of lowering slightly the short run income and interest elasticities, and slowing the implied speed of adjustment. The median lag is six quarters, compared to four quarters in the original results.

Freeland's (1984) preferred equation can best be seen as a distributed lag specification with the lag structure reduced through some (unspecified) procedure so as to include only the first lag of the three interest rates. It is shown as equation FR-1 in Table 3. Perhaps because of the recency of this study, it proved easier to reproduce, with the parameters altering only very slightly.

Pagan and Volker's (1981) preferred equation, using a more general lag formulation, is shown as equation PV-1 in Table 4. We were able to reproduce it satisfactorily. The income and interest elasticities are similar and the speed of adjustment is little changed, with the average lag remaining at four quarters.

Footnotes

It is not uncommon for the interest rate to enter in actual rather than logarithmic form. [5]

An additional difference between Sharpe and Volker's equation and ours is our use of GDP as the income variable whereas their data Appendix indicates that they used GNE. Again, our choice is generated by what gives the closest parameter estimates to those they originally reported. [6]