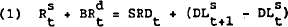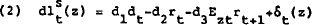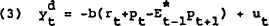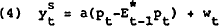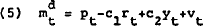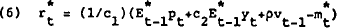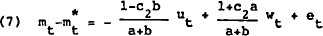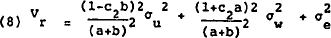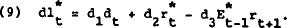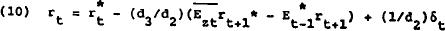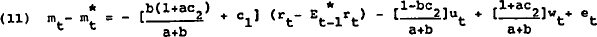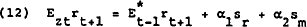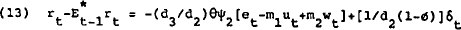RDP 8702: Open Market Operations in Australia: A U.S. Perspective 4. An Economic Model

(a) Overview

The purpose of this section is to consider the theoretical effectiveness of different operating procedures for controlling money. Given that the Reserve Bank employs lagged reserve requirements, the basic instrument of monetary control must be the official market rate. This rate can be used directly or can be used indirectly through the targeting of some reserve measure. The discussion in Section 3 indicates that in Australia the level of banks' loans to dealers is the best approximation of how much discretionary cash balances the banks have at their disposal. That is, banks' loans to dealers can be used as an indicator of the operations required to bring about the desired cash rate. This procedure has some similarities with the Federal Reserve's policy of targeting discount window borrowing. Like the U.S., there is often a conflict between strictly following a reserve quantity objective and maintaining a desired level of interest rates. The following analysis suggests that under existing institutional arrangements in Australia monetary control can best be achieved by the use of an interest rate peg. This contrasts with the results for the United States (see Dotsey (1987)) where an indirect interest rate procedure leads to better results. However, it should be stressed that neither monetary authority follows a pure procedure of pegging the interest rate or of strictly adhering to a reserve target. The analysis below is intended to examine the differences in these two types of pure policies and to, therefore, shed some light on the procedures employed by the Reserve Bank of Australia.

The material in this section is related to the literature on instruments and targets. In terms of that literature the policy maker has a certain goal, say some desired value of real or normal income, and employs an instrument, either the interest rate or the monetary base, that most efficiently atttains that goal. The seminal piece on this topic is Poole (1979) and his analysis has been extended to models employing national expectations by Dotsey and King (1983), (1986) and Canzoneri, Henderson and Rogoff (1983).

However, in this paper which deals with operating policy over a period of two weeks to a month, it is implicitly assumed that there is insufficient information regarding the monetary authority's goal to directly target that goal. Rather the monetary authority chooses an intermediate target, say some monetary aggregate, in order to best achieve its desired policy. A monetary aggregate is chosen because in models employing rational expectations a nominal quantity must explicitly be pinned down for the model to be determinate (see McCallum (1981), (1986)). Again the monetary authority may have a choice as to whether to directly use a reserve instrument such as the base or the interest rate. But in a regime of lagged reserve requirements the base is esentially a state variable and the only choice is some form of an interest rate instrument. The two polar cases considered below are an interest rate peg and an indirect interest rate instrument that involves targeting a reserve measure.

(b) The Market for Reserves

Capturing the major attributes of the Australian money market in an analytically tractable manner requires a degree of abstraction. It is therefore important to isolate the key features that characterise the market for reserves. These features appear to be the presence of lagged reserve requirements, the requirement that banks exchange settlement accounts be non-negative, and the intertemporal decision involved in rediscounting, lender of last resort loans, and bank loans to dealers. In order to capture the intertemporal nature of bank behaviour, it is assumed that the average maturity of a rediscounted security is two periods, where a period would be of the order of one week. Similarly, central bank loans to dealers are assumed to be for two periods. One may also wish to think of the reserve maintenance period as being two periods in length, although this is not crucial. It will be evident for the two alternative operating procedures analysed that the particular reserve accounting regime is irrelevant.

The basic equilibrium relationship in the money market is given by

where 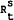are reserves supplied by Reserve Bank open market operations, 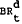is borrowing from the Reserve Bank by dealers plus the volume of rediscounting, SRD_t is the amount of reserves held in statutory reserve deposit accounts, and DL_t are bank loans to dealers. At time t, SRD_t is given and depends on past deposits. Equation (1), therefore, reflects the fact that when reserves are added or subtracted from the system bank loans to dealers respond accordingly.

The important behavioural variable in this relationship is the supply of bank loans to dealers. It is assumed that the quantity of loans is supply determined with dealers accepting any amount of loans at the going rate. Banks hold loans with dealers because funds in exchange settlement accounts do not earn interest. Their inventory of same day funds will be based on the cost of running short. Specifically, if a bank must rediscount a two period security in order to obtain exchange settlement funds the cost is d_t−1/2(r_t+E_tr_t+1) where d_t is the effective rediscount rate and r_t is the rate in the official money market. The expression 1/2(r_t+E_tr_t+1) is the rate that a two period security will earn given effective arbitrage in the money market. The log of the supply of bank loans desired by bank z to dealers is therefore written as

where δ_t(z) is a mean zero independently normally distribute random variable with variance 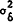and E_zt is the expectation operator conditional on information possessed by bank z at period t. In (2) the coefficients on r_t and ^E_ztr_t+1 are allowed to differ since it is possible that some portion of rediscounting will be done with one period securities.

(c) The Economy^[3]

The model of the economy used is a standard rational expectations model similar to McCallum (1980) involving a basic IS expenditure curve in which the log of output demanded, 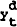, depends negatively on the expected real rate of interest, an output supply function that incorporates the natural rate hypothesis, and a demand for money function. The model is given by

where 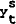is the log of output supplied, P_t is the log of the price level, 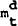is the log of money demand and 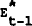is the expectations operator conditioned on information contained in the set 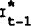. This set is assumed to include all prices, quantities, and random disturbances dated t−1 and earlier. The disturbance terms u_t and w_t are for simplicity independently normally distributed random variables with means zero and variances 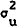and 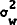respectively. The money demand disturbance displays some persistence and is given by v_t=ρv_t−1+e_t where 0<p<1 and e_t is a mean zero independently distributed random variable with variance 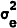.^[4]

(d) An Interest Rate Instrument

One basic means for controlling money is a policy of directly using the interest rate. The efficiency of this policy is measured by the expected squared deviation of money from its target, 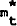. The targeted level of money could arise from some complicated feedback mechanism on past and expected values of various economic variables that are chosen to satisfy broader policy objectives. That is 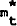should be viewed as an intermediate target. However, the actual choice of 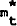is not crucial (see McCallum and Hoehn (1983)), and for simplicity it is assumed that .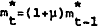

In order to use an interest rate instrument, the Reserve Bank would peg the time t nominal interest rate at a level that will produce 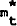in an expected value sense. Hence

where 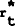is the interest rate objective. Under such a policy, the deviation of money from target can be expressed as

The corresponding expected squared deviation of money from target, V_r is expressed as

(e) A Reserves Objective

Alternatively, the Reserve Bank could attempt to achieve a desired level of money by aiming at a desired reserve measure. That reserve measure is bank loans to dealers. This procedure would amount to an indirect interest rate instrument and involves targeting the level of loans that is expected to produce an interest rate that is consistent with a level of money demand equal to .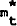

Formally, the targeted level of loans, 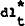, will be

That is, at time t−1, 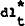is the value of bank loans to dealers that is expected to be consistent with 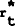and hence 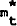. In actuality, the interest rate that yields a value of bank loans to dealers of 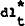will be somewhat different. Combining (2) and (9) yields

where the “bar” over E_zt indicates the average of all bank's expectations. Under this policy the interest rate is allowed to fluctuate around 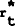due to expectational errors and the random disturbance to the supply of loans.

This policy, therefore, introduces some added volatility into the interest rate. However, whether this policy increases or decreases the precision of monetary targeting depends on the covariance between the interest rate and the aggregate disturbances in the model. This is more easily seen by examining

If, for example, the interest rate were positively correlated with the current innovation in the money demand disturbance then it is possible for the overall effect of money demand shocks on deviations of m_t from 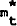to be dampened.

In order to see if this possibility exists, the reduced form expression for the interest rate must be derived. This derivation depends on the information available to agents and the stochastic structure of the model. It is assumed that each bank observes its own balance sheet and therefore observes part of the money stock m_t(z)=m_t+x_t(z), where x_t(z) is a mean zero independently distributed normal variable with variance 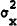. Therefore, bank z's information set, I_t(z), is 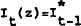plus m_t(z). Regarding the stochastic structure of the model, all shocks with the exception of the money demand shock are white noise.

These assumptions are important if there is to be a possibility for reserve targeting to outperform interest rate targeting. The essential requirements are that the model contain some propagation mechanism and that there is some contemporaneous information available. If, for example, all shocks were white noise and the effects of these shocks were not propagated over time then 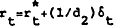. The interest rate would be uncorrelated with the other aggregate shocks in the model and would add variability to the behaviour of money.

Although important, the assumptions are not unreasonable. Agents do obtain contemporaneous information and disturbances are propagated over time. The use of an autoregressive process for the money demand disturbance is merely a simple way of illustrating the mechanism.

In this model banks have two pieces of information that are useful in discriminating among the various shocks. These signals, the interest rate and their own balance sheet, convey a linear combination of the underlying random disturbances. The interest rate conveys the information s_r=ψ₃e_t+ψ₄u_t+ψ₅w_t+ψ₆δ_t, while the balance sheet conveys the signal s_m=−m₁u_t+m₂w_t+e_t+x_t(z). Banks use these signals to calculate E_ztr_t+1 according to

Solving for α₁ and α₂ and using equation (10) yields the reduced form expression (for details see Appendix)

where 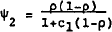. The coefficients θ and ϕ involve ratios of the various variances in the model and take on values between zero and one.

Examining (13) and (11) one observes that the covariances between 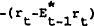and e_t,−u_t' and w_t are all positive. Hence, the particular form of reserve targeting that employs bank loans to dealers unambiguously produces a higher variance of money from target while simultaneously creating additional variability in the interest rate.^[5] This result is just the opposite to that obtained by Dotsey (1987) for borrowed reserve targeting in the United States.

The intuition behind the covariance relationship between 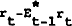and the aggregate disturbances is straightforward. For example, assume there is a positive money demand shock. Banks will perceive part of this shock through the signals s_r and s_m. Also, the positive money demand shock implies that 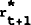will be higher and hence 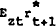rises. This reduces the supply of loans to dealers which means that interest rates must fall for 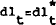. But a fall in the interest rate only exacerbates the increases in money caused by the money demand shock. Therefore, monetary control is lessened.

The above results indicate that from the standpoint of monetary control, a reserves objective is likely to be inferior to an interest rate peg in Australia. In terms of actual operations this would imply that the Reserve Bank of Australia should be more concerned with the interest rate than with bank loans to dealers. The analysis cannot, however, explain the actual procedures used in Australia which fall somewhere between the two policies and which therefore allow a certain amount of daily interest rate volatility. In order to completely analyse the introduction of variability would require a more detailed dynamic model with explicit references to public and private welfare functions. Models such as Cukierman and Meltzer (1986) and McKibbin (1987) provide reasons (although different ones) as to why noise or ambiguity may be introduced into policy. The purpose of this analysis is to provide a detailed description of the two types of policies that span the actual policy employed by the Reserve Bank of Australia.

Footnotes

The model used represents a closed economy. Extending the result to open economy would be of interest but the basic mechanism that drives the results does not seem to be sensitive to such an extension. [3]

A degree of permanence could be modelled for the other variables without affecting the qualitative results. [4]

With respect to the variability of output, 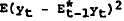. as long as 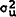does not dominate all the other variances, then a peg is more efficient. [5]