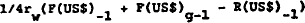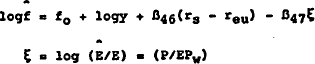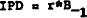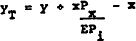RDP 8710: Transmission of External Shocks in the RBII Model 2. Structural Adjustments
November 1987
- Download the Paper 753KB
In order to limit the possibilities for arbitrary changes to the model, we have tried to adhere to the principle of making minimal structural adjustments to RBII consistent with attaining a small number of clearly defined objectives. These objectives weret
- greater interest rate flexibility, particularly in short-term rates;
- full endogeneity of debts and of debt service costs;
- dynamic Stability.
An additional adjustment, discussed in Section 2.3, incorporates a measure of output adjusted for the terms of trade into the model. However, equations for the real sector, which presumably is least affected by deregulation, remain substantially unchanged from those given in Fahrer and Rankin (1984).[2] Some “tuning” of the new parameters was carried out using simulation analysis to check that the above objectives were satisfied, and that the economic responses for the model as a whole appeared sensible.
This section describes in detail the most important differences between our model and the 1984 version. The full model specification is given in Appendix 1.
2.1 Interest Rate Equations
Traditionally the RBII model has specified all interest rates as partial adjustment processes. This reflected the institutional fact that, for most of the 1970's, bank interest rates were subject to regulation, and interest rates on government securities were administratively determined. Consequently, interest rates in RBII were not regarded as market clearing prices in the short run. The 1984 version of the model respecified the bond rate equation to be consistent in the long run with quantity setting, rather than price setting, operations by the central bank; however a partial adjustment process on the bond rate was retained. Other interest rates in the model were determined by slow adjustment towards weighted averages of the bond rate and exogenous overseas rates. In simulation the structure generated quite slow interest rate responses to changes in policy variables and in external conditions.
It has become clear that this kind of structure is no longer an accurate representation of interest rate determination in Australia. At the short end of the market, interest rates are now highly flexible in clearing the market for short-term funds. In recognition of this, short-term interest rates are now determined in a clearing cash market.[3] The cash market is defined by two equations (numbered as in the model specification in appendix 1).
Central bank balance sheet indentity (supply of cash):
| where | G | = | nominal government expenditure (=Pgg1 + Pg2 + Pc) |
| T | = | nominal tax revenue (= T1 + T2) | |
| IPD | = | interest on public debt | |
| B | = | stock of government securities held by the private sector | |
| R | = | foreign exchange reserves | |
| D | = | differential operator |
Demand for cash:
| where | rs | = | short-term interest rate |
| M | = | money stock (M3) |
The demand for cash is thus a function of a scale variable (the money stock) and the short-term interest rate. The short-term interest rate is thought of as representing either a 90 day bill rate or an average cash (overnight) rate over a period of one quarter. Equations (17) and (20) are intended to capture some essential features of the deregulated money market. With a freely floating exchange rate, the variable defined by (17) is controllable, and can be used as an instrument to influence short-term interest rates. Rates respond flexibly to clear the cash market in each period.
The introduction of a clearing market for a very narrow cash aggregate is in some ways a departure from earlier formulations of the RBII model. Taken in conjunction with the floating exchange rate, as introduced in the 1984 version, we now have a small but highly important sector of the model which is always in (partial) equilibrium. This departure is a recognition of changed circumstances in both markets, and should not be viewed as inconsistent with the general disequilibrium underpinnings of the model as a whole. In particular, the cash market does not equilibrate the demand and supply of the conventional monetary aggregates, and the buffer stocks of money and inventories continue to play an essential role in the dynamics of the model. In specifying a small subset of clearing markets within a context of lagged adjustment in the economy as a whole, EBII is consistent with many conventional open economy models (for example Dornbusch (1976)), which typically assume continuous partial equilibrium in some financial markets, while allowing other markets to be temporarily out of equilibrium.
The cash market submodel determines the short-term interest rate. The long-term rate is determined by the equation
ie, as a long-run weighted average of short-term rates. In the long run, this equation is consistent with the expectations theory of the term structure, since it requires an elimination of divergences between the two rates in the steady state.[4] This consistency would carry over to the short run if expectations about future short rates were formed adaptively.
The above equations are sufficient to determine the partial equilibrium values for interest rates, given the market operations of the central bank. It remains for us to define a rule for determining those operations. In principle, any well defined rule would suffice to complete the monetary sector of the model. For the purposes of this paper, we define market operations as a linear function of five indicator variables: the inflation rate, the rate of GDP growth, the rate of money supply growth, the short interest rate, and the exchange rate. Policy regimes in which market operations are a function of the interest rate or the exchange rate alone, can be considered as special cases. This is not intended as an attempt to represent actual policy rules, but as an example of how a policy rule can be assumed to close the model.
2.2 Debt Accumulation and Debt Servicing
The RBII model contains two important debt variables: these are the stock of government bonds, and the stock of net external debt. Servicing costs on both debts have usually been treated as exogenous.[5] For short-run analysis this is probably a useful simplification, but the assumption becomes increasingly unrealistic for analysis over longer time horizons, particularly in periods when current account and budget balances are not close to zero.
(a) External debt
In the case of external debt, two adjustments are necessary. First, the capital flow equilibrium condition and the balance of payments identity are rewritten in US dollar, rather than Australian dollar, units. Assuming for the purposes of the model that all external debt is denominated in foreign currencies,[6] this allows us to calculate the endogenous debt servicing term as a product of the quarterly interest rate and the net external debt in US dollars. Thus the term
is added to the current account, where
| rw | = | “World” interest rate (10 year US bond rate) |
| F | = | external private sector debt in $A |
| Fg | = | external public sector debt in $A |
| R | = | foreign exchange reserves, valued in $A |
| (US$) denotes valuation in US$ by dividing the relevant variable by the exchange rate. | ||
The second adjustment involves recognising the implications of exchange rate movements for the valuation of the stock of external debt. The capital flow equation (equation 14) is expressed as a partial adjustment towards the desired stock of debt in US$, rather than $A, units.
| where | y | = | output |
| P | = | price level | |
| E | = | exchange rate | |
| Pw | = | World price index | |
| reu | = | eurodollar interest rate. |
In this revised specification, behaviour is governed by adjustment towards the equilibrium value of net debt in real Australian dollars. Changes in the exchange rate will influence this behaviour both through the conventional expectations effect, captured by the term ξ, and through the revaluation of the existing stock of debt, which directly affects the ratio of desired to actual debt in Australian dollars.
(b) Public Debt
Endogenous public debt is included in the model using the formula
| where | IPD | = | nominal interest on public debt |
| B | = | nominal stock of bonds held by the private sector | |
| r* | = | weighted average interest rate on bonds outstanding. |
The average interest cost r* is not of course directly observable, and is approximated by a distributed lag of past values of rι. A strictly accurate measurement of this cost would require a complicated disaggregation of the stock of bonds by issue date, in order to determine the exact weights on past interest rates; this refinement seems unlikely to yield important gains in accuracy and has not been attempted. (The simplification used here was suggested by Helliwell (1977)).
Recent literature on debt financing has highlighted an important source of potential instability in models with endogenous debt servicing costs.[7] With constant monetary and fiscal policies, a given stock of debt will automatically grow at a rate of r*, as the debt is rolled over in each period and new debt is added to cover interest payments. If the interest rate is higher than the economy's natural growth rate, the debt to GDP ratio in such a model will grow without bound. Typically this accumulation is very slow and can be safely ignored when considering questions of a purely short-run nature. In general however the debt accumulation problem represents a powerful argument against the long-run exogeneity of monetary and fiscal policies. He would expect policy variables to react so as to ensure that the debt to GDP ratio is bounded, a result which may be achieved either by long run monetisation of debt, or by fiscal action to ensure that debt service costs are at least partly tax-financed.
In order to accommodate this argument, we postulate that one of the following reaction functions operates.
| (i) | Dlogg1 | = | −Jβ58 Dlog(B/Py) | β58 > 0 |
| (ii) | Dt11 | = | Jβ59 Dlog(B/Py) | β59 > 0 |
| (iii) | Dλ2 | = | Jβ60 Dlog(B/Py) | β60 > 0 |
| where | g1 | = | real government current spending |
| t11 | = | income tax rate | |
| λ2 | = | permanent growth rate of money stock[8] | |
| J | = | dummy variable equal to zero for the first n periods, increasing smoothly to one thereafter. |
The J variable incorporates an arbitrary assumption about the length of time that is allowed to elapse before the debt to GDP ratio influences policy settings in the model. These reaction functions provide us with a framework for addressing questions concerning the long-run implications of fiscal policy in a consistent way.
2.3 A measure of the value of output adjusted for the terms of trade
The Australian Statistician[9] has recently begun publishing a series on the real value of output adjusted for the terms of trade. In the terminology of RBII, we define this measure as
| where | yT | = | real output adjusted for the terms of trade |
| y | = | real GDP | |
| x | = | exports at constant prices | |
| Px | = | price of exports | |
| Pi | = | price of imports |
The variable yT is intended to measure the purchasing power of national income, which will differ from the standard measure of constant price GDP when substantial variations in the terms of trade occur. In order to capture the effects of movements in the terms of trade on consumer demand and on investment, it is the adjusted variable that we use to measure output in the consumption and investment equations.
Footnotes
Hereafter, the “1984 version” of RBII. [2]
A detailed account of the operation of the cash market in Australia is given in Reserve Bank (1985). For the purposes of the RBII model, the aggregate “cash” corresponds with banks' currency holdings, exchange settlement accounts, and deposits with authorised dealers. Since the latter are not modelled, their accounts are treated in RBII as though consolidated with the central bank. [3]
Empirical work on the term structure by Tease (1986) supports the expectations hypothesis in Australia in both the short run and the long run. [4]
Public debt interest was endogenous in the 1976 model specified by Jonson, Moses and Wymer (1976) but this feature was dropped from later versions. [5]
In fact the ratio is about three quarters. [6]
Buiter (1981) provides a comprehensive analysis of these issues. [7]
λ2 is normally regarded as a constant. In order to allow for endogenous inflation when this reaction function is used, λ2 is made an endogenous variable. This has meant that the effects of changes in λ2 on the constant terms in equations for endogenous nominal variables, and on the values of exogenous nominal variables, have had to be explicitly specified. [8]
Quarterly Estimates of National Income and Expenditure, March Qurter, 1986 (ABS 5206.0) [9]