RDP 8804: Pricing Behaviour in Australian Financial Futures Markets 6. Empirical Results
June 1988
- Download the Paper 943KB
6.1 Some Descriptive Statistics
Because of the potentially large impact of the share market crash on any statistical results, all tests are reported for both the complete sample available at the time of writing (the sample runs from December 1984 to February 1988) and a “pre-crash” sample which ends at September 1987. As a preliminary to the main hypothesis tests, Tables 2 and 3 present some descriptive statistics on the properties of the first-differenced time series for spot and futures prices. For the purposes of this section, all variables are measured in logs. (Bill and bond yields are converted to log prices by taking the log of one plus the yield in each case.) To remove the “new contract” effects referred to in section 5.1, the futures data are pre-filtered by regressing the series on a full set of new contract dummies. Under the null hypothesis, the first differenced pre-filtered futures prices are white noise. This is not necessarily true for spot prices.
The autocorrelations and partial autocorrelations given in Tables 2 and 3 show that these series are clearly stationary in first differences, and suggest that they are generally close to being white noise, though there are some lag lengths at which correlations are marginally significant. There is, for example, significant first-order autocorrelation in futures prices in one case (that of 10 years bonds) but this appears to be sensitive to the length of the sample period chosen, and becomes insignificant when the crash period is removed from the sample. At longer lag lengths, the main feature of interest is a possible indication of fourth-order autocorrelation in spot interest rates, suggesting a weak within-month seasonal pattern.[3] This is not necessarily evidence of inefficiency, although there is weak evidence that this pattern may carry over into futures prices, which would be inconsistent with efficient markets. This proposition is more formally tested at a later point.
Table 4 presents tests of the hypothesis that innovations in futures prices are normally distributed (see Bera and Jarque (1986)). This is of only passing interest for the main questions in the present study, but is highly relevant in considerations of portfolio choice involving futures markets, and in the pricing of options on futures. Bera and Jarque specify a normality test which is a weighted combination of tests for skewness and kurtosis proposed by D'Agostino and Pearson (1973). The individual test statistics for skewness and kurtosis are given along with the combined test. The results reported in Table 4 suggest that interest rate futures prices come from distributions which have higher kurtosis (ie are more peaked) than the normal, but are not significantly skewed. Roughly speaking, this means that large price changes occur with greater frequency than would be the case if the underlying distribution was normal. For SPI futures the results depend, not surprisingly, on whether or not the period around the share crash is included in the sample. The pre-crash data suggest consistency with the hypothesis of normality, but the October movements in share prices are sufficient to refute the hypothesis decisively, if included in the sample. A crash of the magnitude which actually occurred has virtually a zero probability of being drawn from a normal distribution.
6.2 Efficiency
Informational efficiency is tested using equation (4) as outlined in the previous section. The test involves specifying an arbitrary set of “Z” variables which are predetermined at time t, as possible predictors of the futures price movement (ft+1−ft). Two sets of tests are reported. The first uses lagged changes in spot and futures prices in the predetermined variable set; lags of up to 5 weeks are included, so as to make it possible to detect any inefficiency arising from within month seasonality. The estimated equations are reported in Tables 5 (for the pre-crash sample) and 6 (full sample). The results show little clear evidence of inefficient pricing, with only 3 out of 60 reported coefficients being significant at the 5 per cent level. Of these, the constant term in the SPI equation is highly significant and positive in the pre-crash sample, indicating positive drift in futures prices. This means that on average, an uncovered long position in SPI futures earned significant positive profits over the period, which is inconsistent with market efficiency.
One way of reconciling this result with investor rationality would be to hypothesise a speculative bubble of the form originally suggested by Blanchard (1979). Blanchard attempted to formalise the notion of a price which remains above market fundamentals for a sustained period because it is expected to grow further. In a process of this kind, it is assumed that the “bubble” is expected to grow at each point in time with some probability (1−π), but that the price returns to fundamentals with probability π. Expected capital growth must be just sufficient to ensure that investment in the market is a fair bet in each period. In the presence of this kind of bubble, the market would appear to be inefficient in any sub-period in which the bubble is still growing, because the return to a long position would contain a positive premium offsetting expected losses when the price returns to fundamentals. This hypothesis is not dissimilar to the “Peso problem” which arises in relation to forward exchange markets. In a loose sense, the hypothesis is supported by the result for the full sample, in which the constant term becomes insignificant; the crash was of roughly sufficient size to reduce the average excess returns on a long futures position to zero in the period taken as a whole.
Other significant coefficients in the above set of equations are fourth lags in the bill futures equation (pre-crash) and SPI futures equation (full sample), but these are only marginally significant and may well be spurious, given the large number of estimated coefficients.
The second set of efficiency tests uses expected premiums (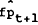 −
fpt) in the predetermined variable set. This test is specifically designed to test
whether information about time to maturity (ie. the predicted rate of convergence between
futures and spot prices) can be used to help predict the change in futures prices. The method of
constructing an instrument for the expected change in the premium (
−
fpt) in the predetermined variable set. This test is specifically designed to test
whether information about time to maturity (ie. the predicted rate of convergence between
futures and spot prices) can be used to help predict the change in futures prices. The method of
constructing an instrument for the expected change in the premium (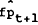 −
fpt) was outlined in Section
5. Results are shown in Table 7, and indicate no
significant departures from efficiency, other than the positive constant term in the SPI
equation which has already been discussed. An interesting consequence of these results is that
spot prices must contain a predictable component which is offset by predictable movements in the
premium. This is not necessarily evidence of spot market inefficiency. It simply indicates that
future systematic behaviour of spot prices (whatever the cause) is rationally incorporated into
current futures prices, whether or not the spot market itself is fully efficient.
−
fpt) was outlined in Section
5. Results are shown in Table 7, and indicate no
significant departures from efficiency, other than the positive constant term in the SPI
equation which has already been discussed. An interesting consequence of these results is that
spot prices must contain a predictable component which is offset by predictable movements in the
premium. This is not necessarily evidence of spot market inefficiency. It simply indicates that
future systematic behaviour of spot prices (whatever the cause) is rationally incorporated into
current futures prices, whether or not the spot market itself is fully efficient.
6.3 Price Volatility
This section reports results on the three sets of hypothesis tests described in Section 5.2. The first two hypotheses concern changes in the variance of spot prices through time, and involve testing whether or not such changes are associated with lagged or contemporaneous activity on futures markets. The third concerns the related question of the lead-lag relationship between futures and spot prices in levels. Since the first two of these tests hypothesise the existence of conditional heteroskedasticity in the spot price data, a useful first step will be to test for this. A useful test in this regard is the ARCH test for conditional heteroskedasticity proposed by Engle (1982).
The ARCH test specifies conditional heteroskedasticity of the form
where εt is a zero mean error term; a X2 test is applied for the joint significance of the β coefficients. Thus, the ARCH method tests whether past variation in the error terms helps to predict the variance in the next period. Results are shown in Table 8. Lag lengths in each case were determined by testing down from a lag length of 6. The results show significant heteroskedasticity in two of the three cases, the exception being the share price index.
Results concerning the three main hypotheses on price volatility are reported in Tables 9 and 10. The first hypothesis is that futures trading volumes have a significant influence on the conditional variance of spot prices. As the results in Table 9 show, this hypothesis is rejected in the case of the two interest rate contracts: for these there appears to be no statistical relationship, either lagged or contemporaneous, between futures trading volumes and spot volatility, at least at the level of weekly data. One point to note on this issue is that the Wednesdays sample used here excludes certain days of high average volatility, such as balance of payments “news” days (which are generally Tuesdays), and it is possible that a correlation between price movements and volume could be detected on those days if both are similarly influenced by news. The result reported here does not rule out such correlation, but does appear to reject a causal link from volume to volatility.
In the case of the SPI, the results are ambiguous. There is an estimated negative contemporaneous relationship between volume and volatility, but this could easily be spurious, since the coefficient on the first lag is almost equal and opposite to the contemporaneous coefficient. No relationship is detected when the first lag is dropped from the regression.
The second and third hypotheses are closely related, asserting that futures markets lead spot markets in terms of price variability, and price levels, respectively. Test statistics for the two hypotheses are likely to yield similar results, since a lead-lag relationship established in terms of price movements is likely to carry over when measured in terms of the squared values of those price movements. This close relationship is born out by the results in Tables 9 and 10. There is quite strong evidence that futures prices lead spot prices (in both senses) for the two interest rate contracts. The lag lengths, at up to two weeks, are surprisingly long, although the strongest effects are contemporaneous or at the first lag. The evidence is much weaker for the SPI contract, with only the first lag in levels being significant, and only for the pre-crash sample. In the case of the bill contract, the interpretation of the empirical lead-lag relationship is somewhat ambiguous, since it may be evidence that the futures price innovation is predicting a movement in short-term interest rates which is outside the maturity period of the currently traded bills. This explanation may account for some part of the detected lead-lag relationship in this case.
Footnote
This may be due to seasonality in government receipts and payments. [3]
