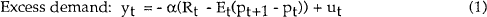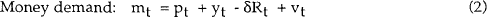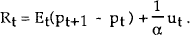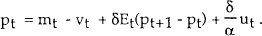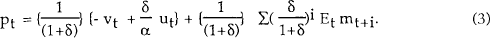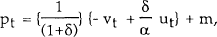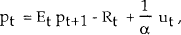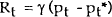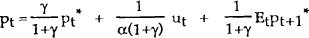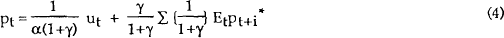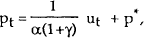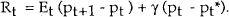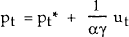RDP 8905: Monetary Policy Instruments: A Theoretical Analysis 2. Price Level Determination in a Simple Model
July 1989
- Download the Paper 571KB
The following two equation system represents a “simplest possible” neoclassical model of the macroeconomy.
| where | yt | is the log of real demand at t |
| mt | is the log of the nominal money stock | |
| pt | is the log of the price level | |
| Rt | is the nominal interest rate. |
All variables are measured as deviations from steady state values. It is assumed that output supply is fixed, so that the market clearing condition yt = 0 is satisfied in each period.
The above model is chosen not for purposes of realism, but because it permits a number of important conclusions concerning money and interest rate rules to be illustrated in fairly simple fashion. Moreover, it does so in a dynamic framework which in principle is least favourable to interest rate rules, so that any support for the latter should not be interpreted as arising from bias in the model specification. Of the simplifying assumptions, that of fixed output supply is probably the most unrealistic, and a more realistic model with variable output and inertia is introduced in section 5.
Using the market clearing condition that yt = 0, the output variable can be eliminated from equations (1) and (2), leaving a two equation system with three endogenous variables: money, prices and the interest rate. A third equation is needed to complete the system, and this may take the form of a monetary policy rule specifying the time path of either the money supply, or the nominal interest rate. These two possibilities are considered in turn.
(a) A money supply rule
The aim is to solve equations (1) and (2) to obtain an expression for the price level and the interest rate as functions of the money supply and the exogenous shocks.
From equation (1), the equilibrium nominal interest rate is given by:
This can be substituted into the money demand function to obtain what is a fairly standard equation for the price level, as a function of the money supply and expected future prices:
By repeated forward substitution, this gives the solution
The equilibrium price level is thus equal to a discounted sum of expected future money supplies, plus a sum of current real and financial shocks.
Expected future money supplies in the above equation are determined by the form of the money supply policy rule. The simplest special case is when the money stock is held constant, so that mt = m. In this case, equation (3) reduces to
so that the price level is proportional to the money stock, and fluctuates randomly around the steady state according to the real and financial disturbances in each period.
(b) An interest rate rule
It can be readily seen from equation (1) that a policy rule which exogenously sets the interest rate has no determinate solution for the price level. This follows from the fact that the equation can be written as
which does not allow pt to be expressed as a convergent sum of the exogenous variables. The same result applies if the interest rate is made a function of real demand. However, the price level can be tied down if the policy rule for Rt responds dynamically to a nominal variable (either mt or pt). Since the assumed objective of policy is to stabilise prices rather than money, it is useful to consider the case where the price level is the target variable.
Suppose a policy rule of the form
is used, where pt* is the price level target. The rule states that when prices are above target, policy raises the nominal interest rate. This can be substituted into equation (1) to obtain
which is exactly analogous to the earlier case where prices were expressed as a function of money. The solution to this equation is
which expresses the equilibrium price level as a function of its current and expected future target values. As in the case of a money rule, the exogenous nominal target path is assumed to be set by the monetary authority. In the special case where the target price level is constant, the solution reduces to
so that the price level fluctuates randomly around the target in response to real shocks.
An important feature of this analysis is that under an interest rate rule with price level target, the money demand function plays no part in determining either prices or the interest rate; its only role is in determining the stock of money once these other variables have been determined. The mechanism for price level determination lies in the goods market. Prices jump in response to shocks to excess demand, adjusting so as to clear the goods market given information about the nominal interest rate and expected future movements in prices. Two conditions are necessary for this mechanism to work. First, real demand must be sensitive to the real interest rate; and secondly, the policy target must be expressible in terms of a nominal level.
An alternative way of specifying the policy rule which should also be considered is to allow the nominal interest rate to respond to expected inflation. This is represented by a policy rule of the form
In this case the solution can be obtained directly from substitution into equation (1), giving
provided the response parameter γ is non-zero. This illustrates that, like the fixed nominal interest rate policy, a fixed real interest rate policy is insufficient to tie down the system. The policy rule must give some weight to a target expressible as a nominal level.