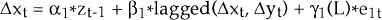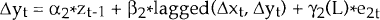RDP 8910: An Analysis of the Determinants of Imports 4. Functional Form

In most previous attempts to model imports it has been implicitly assumed that all variables used as explanators in the regression exhibit stationarity. That is, the distribution of each variable is assumed to be constant and thus its mean and variance do not change over time. This property ensures that any sample mean and variance gives a true representation of the population mean and variance for a series. In addition, errors from regressions involving only stationary variables must themselves be stationary. When variables are non-stationary, conventional econometric results must be interpreted with care as the classical assumptions about the behaviour of the random variables used in the regression no longer hold. Although the coefficient estimates from such regressions are consistent^[7], the test statistics have non-standard distributions.

There are two ways of dealing with non-stationary variables in order to use standard regression techniques. The first is to manipulate the non-stationary data series in order to make them stationary. This may involve detrending or differencing the series, depending on the type (stochastic or deterministic) and order of non-stationarity. The major problem with manipulating data series in this manner is that information is lost – one cannot infer the long run steady state relationships between variables from the estimated model.

Until the mid 1980s this was the approach which economists tended to follow. However, following some important advances in econometrics, it became possible to test whether any of the non-stationary series are cointegrated with each other. Cointegration techniques attempt to model the long run steady state relationships. If variables are cointegrated it means that although the individual time series exhibit non-stationary properties, linear combinations of these variables exhibit stable properties. We would generally expect economic theory to explain why these variables move broadly together over time.

In this paper, when analysing the time series properties of our random variables, we look only at the first two moments of their distributions. A non-stationary random variable is defined as one which does not have a constant mean and/or variance over time. If it is necessary to difference a series d times to make it stationary then the series is defined as being integrated of order d, denoted (d). Stationary variables are therefore I(0).

If two variables, x_t and y_t, are cointegrated, then the residuals from a regression of x_t on y_t must be stationary, i.e. I(0). Â, the estimated coefficient on y_t from this regression, is known as a ‘super consistent’ estimate^[8]. However, because x_t and y_t are I(1), Â's standard error has an unknown distribution. Therefore Â's t-statistic cannot be usedas a test of significance.

If  is the estimated coefficient on y_t from a regression of x_t on y_t, then x_t=Â*y_t is the estimated long run equilibrium relationship between x_t and y_t. In any period the residual, z_t = x_t − Â*y_t, measures the extent to which the system deviates from the estimated long run equilibrium in that period.

Engle and Granger (1987) showed that once a number of I(1) variables have been shown to be cointegrated, there always exists a system of equations having error-correcting form which represent the dynamics of the series. The error-correction representation implies that changes in the dependent variable are a function of the level of disequilibrium in the cointegrating relationship – that is the departure from the long run equilibrium – as well as changes in other explanatory variables.

More formally, assuming once again that two variables x_t and y_t are both integrated of order 1 and assuming they are cointegrated, so that z_t = x_t − Â*y_t is I(0), then Engle and Granger proved that it must be the case that:

and

Within this system of equations, at least one of the coefficients on the cointegrating term, z_t−1, must be non-zero.

The equation for Δx_t can be estimated by OLS, in isolation from the equation for Δy_t, because none of the explanatory variables in either equation are contemporaneous with the error terms. The standard t-tests of significance on the variables are also valid, since all of the regressors in this equation are I(0).

We can think of this equation as having both short run and long run components. The term z_t−1, measures the extent to which the system, that is x_t−1 and y_t−1, deviates from its long run equilibrium relationship, i.e. x_t−1 = Â*y_t−1. If the system is stable, α₁, the coefficient on z_t−1, will be negative.^[9] Then, when z_t−1 is non-zero – i.e. when x_t−1 is different from Â*y_t−1 – the term α1*z_t−1 acts to bring the system back towards its long run equilibrium. Thus, the size and sign of z_t−1, the previous equilibrium error, influences the magnitude and direction of movement in x_t.

The short run dynamics are captured in the full equation. Having imposed the cointegrating relationship, the coefficients on the lagged differenced series influence the path of adjustment back to equilibrium of the dependant variable.

Footnotes

That is, given a relationship y_t = α + βx_t + ε_t, where ε_t has standard properties and x_t is stochastic, then the OLS estimate, 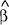, will be a consistent estimator of β as long as E(x'ε)=0. [7]

Super consistency refers to the fact that the estimate, Â, converges to its true value, A, at a rate faster than standard OLS estimates. This implies that one can be confident of the accuracy of coefficient estimates from cointegrated regressions. See Pagan and Wickens (1989). [8]

α₁ can be zero. This possibility is ignored because it complicates the argument without making any substantive difference. [9]