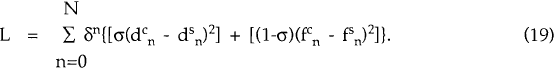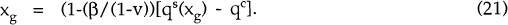RDP 9001: Is Pitchford Right? Current Account Adjustment, Exchange Rate Dynamics and Macroeconomic Policy 4. Welfare and Policy
May 1990
- Download the Paper 955KB
The general result that emerges from section 3 is that the dynamic path for all variables is different when the real exchange rate is slow to adjust, but why should we care about that ? After all, the current account becomes balanced eventually, and isn't that the focus of our concerns ? The answer to these questions is that the distorted adjustment path for the real exchange rate leads to a problem of resource misallocation that ought to be of concern to policy makers.
This is a matter of elementary welfare economics. Domestic consumption of the two goods in this model is a function of their relative price, q. Distorted values of q must therefore lead to distorted consumption levels, in each period, of domestic and foreign goods. The result is a lower level of welfare than would be the case if the economy were free of such distortions. Since the current account is a function of the consumption levels of the two goods, it also follows a distorted sub-optimal path.
To gain an idea of the quantitative effects of this distortion, consider the following loss function:
δ = 1/(1+r) is a discount factor and the c and s superscripts, respectively, refer to the market-clearing and sticky real exchange rate values of d and f. The deviations of d and f from their optimal values are weighted by their shares in total consumption. L is the discounted sum of welfare losses that arise when the consumption of each good deviates from its Pareto-efficient level in each period.
Table 1 gives outcomes for L, over a twenty-year horizon, for different values of γ and u. Not surprisingly, the largest losses occur when γ = 0.25, i.e. when the real exchange rate is slowest to adjust. There is no general tendency, however, for welfare losses to be significantly smaller as u increases for a given value of γ. For given values of u and γ welfare losses are significantly greater when the shocks occur to the demand for domestic goods (x and y) than when they occur to the demand for foreign goods (z). [17]
| γ | ||||
|---|---|---|---|---|
| x=0.2 | 0.25 | 0.50 | 0.75 | |
| 0.25 | 2.36 | 0.76 | 0.17 | |
| u | 0.50 | 1.90 | 0.66 | 0.15 |
| 0.75 | 1.59 | 0.59 | 0.14 | |
| y=−0.2 | ||||
| 0.25 | 3.07 | 0.86 | 0.18 | |
| u | 0.50 | 2.87 | 0.81 | 0.17 |
| 0.75 | 2.69 | 0.76 | 0.16 | |
| z=0.2 | ||||
| 0.25 | 0.28 | 0.04 | 0.01 | |
| u | 0.50 | 0.43 | 0.07 | 0.01 |
| 0.75 | 0.50 | 0.09 | 0.01 | |
* × 100 |
||||
Since the sticky real exchange rate outcomes are inefficient, policy has the potential to enhance social welfare. The purpose of this government intervention should be to restore consumption of each good to its Pareto-efficient level. While the current account, as such, ought not to be the object of government policy (since the current account does not enter anybody's utility function) the effect of government intervention will be to alter the current account outcome.
One obvious role for policy would be to try to reduce the degree of real exchange rate inflexibility; this might be achieved by various pieces of “microeconomic reform”. However, since there are good reasons to believe that even markets with no institutional rigidities will exhibit a certain degree of price inflexibility (see n.13) there is a limit to the extent to which microeconomic policy will alleviate the problem.
What about macroeconomic policy, specifically, fiscal policy ? When the real exchange rate is sticky an optimal fiscal policy leads to a replication of the market-clearing outcome, in each period, for private spending on domestic and foreign goods. Fiscal policy in this model is effected by exogenous changes in public spending on domestic goods and/or foreign goods. This leads to changes in the real exchange rate and hence to changes in the level of private consumption of each good.
Suppose that the only fiscal instrument that the government can use is exogenous spending on domestic goods; let this spending be denoted xg. Using (1) and (5), it turns out that dc = ds(xg), for all three kinds of spending shocks, if
where ds and qs are both functions of xg. A closed-form solution for xg can be found in terms of the parameters β, σ, r and u. (Of course, both qs and qc will be different under each of the shocks and so the solutions for xg will also be different).
Using (3) and (5), the spending rule that equates fc = fs(xg) can also be found:
Obviously, (20) ≠ (21), and so it is not possible for variations in public spending on domestic goods to lead to optimal levels of private consumption of both domestic and foreign goods.
Suppose, however, that public spending on foreign goods (denoted zg), is also available as a fiscal instrument. Equality of dc and ds is implied by the fiscal rule
while equality of fc and fs is implied by
Equations (22) and (23) indicate that, under an optimal fiscal policy, xg = 0. Appropriate amounts of public expenditure on foreign goods alone will lead to a replication of the market-clearing real exchange rate. This leads to optimal (welfare-maximizing) amounts of private expenditure on both domestic and foreign goods.[18] The market-clearing current account will not be replicated, but this in itself has no welfare implications.
Although a current account imbalance is self-correcting, an appropriate macroeconomic policy will improve social welfare. This policy leads to changes in private consumption levels, and as a result, alters the current account outcome. Commensurate changes in the real exchange rate lead to the new current account balance being validated by appropriate variations in exports and imports.
Footnotes
One of the major costs of a distorted real exchange rate that is not considered here is the likelihood that it results in irreversible investment in the wrong parts of the economy. (See Alesina et al (1990)). This failure of the price mechanism to impart the correct signals could well lead to large dynamic inefficiencies and so Table 1 almost certainly underestimates the welfare costs of a sticky real exchange rate. [17]
From standard duality methods, we know that when utility is maximized, U(d,f) = V(q,y), where U(·) is the direct utility function, V(·) is the indirect utility function, and y is income. Thus, with income constant in this model, the welfare-optimizing levels of d and f are obtained at the market-clearing real exchange rate qc. [18]