RDP 9009: An Empirical Model of Australian Interest Rates, Exchange Rates and Monetary Policy 4. Results
November 1990
- Download the Paper 730KB
a. Testing for a Structural Break
The first task was to confirm that a structural break did in fact take place around October 1987. This required us to choose a day in that month as our postulated break point. Quite arbitrarily, we chose October 20, giving 710 and 575 observations in the first and second periods, respectively.[8] We tested for structural stability by estimating unrestricted and restricted VAR systems, the restrictions being that the parameter values in the VAR did not change at this break point.
The unrestricted VAR takes the form Y = (B + AD)X, where D is a matrix of dummy variables, [dij] = 1 from October 21 1987 onwards. Each equation contains 10 lags of each of the variables, plus a constant. The test of structural stability is the test that the coefficients aij are jointly equal to zero. The test was conducted by constructing the statistic
where T is the number of observations in the full sample and |Σ1| and |Σ2| are the determinants, respectively, of the covariance matrices of the restricted and unrestricted VAR systems estimated over the entire sample period.
Z is distributed as Chi-square with degrees of freedom equal to the number of restrictions; in this case, with five equations, five variables and 10 lags, there are 255 restrictions. Our estimated value of Z is 1,268, which exceeds the five percent critical value of 293, and so we reject the hypothesis of structural stability.
Given the existence of a structural break, we then estimated two VARs. The sample periods were January 2 1985 to October 20 1987 and October 21 1987 to January 30 1990, respectively. We do not report the parameter estimates since they are of no intrinsic interest. They are available on request.
b. Impulse Responses
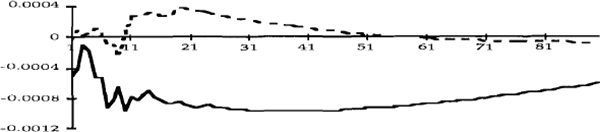
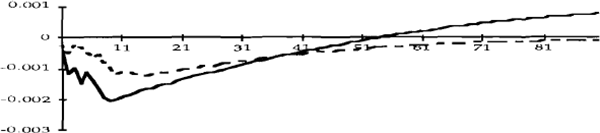
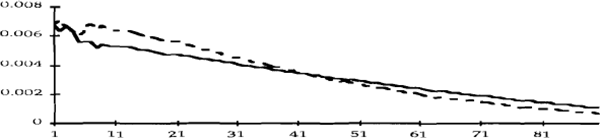
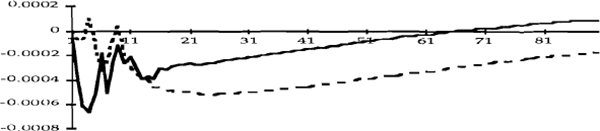
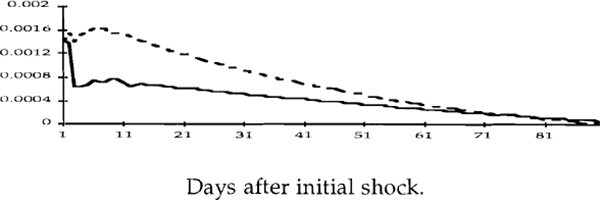
Figures 2a to 4e show impulse response functions of the domestic variables in response to a one standard deviation shock to each of the variables. These are calculated over a 90 day horizon. Each figure contains two lines, the dashed line refers to the first period and the solid line refers to the second. The vertical axes show the responses of the variables to the various shocks, while the horizontal axes denote elapsed time, in days.[9] To facilitate comparisons, the impulse responses in each figure have been scaled so that they reflect shocks of the same size.
Cash rate responses to one standard deviation shocks
| ----Period one (2/1/85 – 20/10/87) |
____Period two (21/10/87 – 30/1/90) |
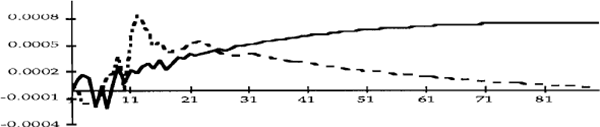
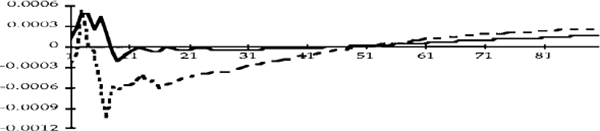
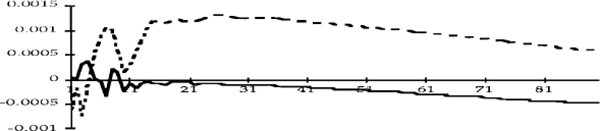

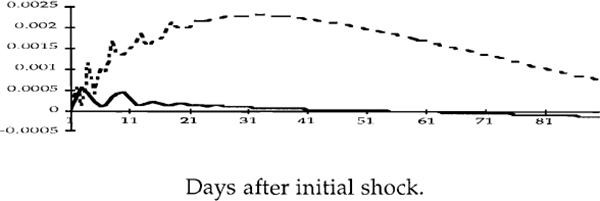
Exchange rate responses to one standard deviation shocks
| ----Period one (2/1/85 – 20/10/87) |
____Period two (21/10/87 – 30/1/90) |
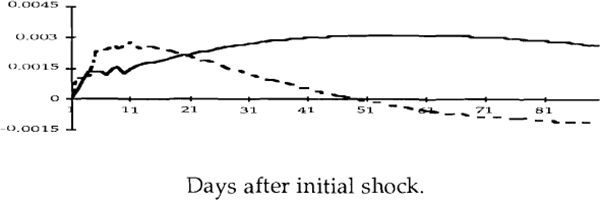
Australian bond rate responses to one standard deviation shocks
| ----Period one (2/1/85 – 20/10/87) |
____Period two (21/10/87 – 30/1/90) |
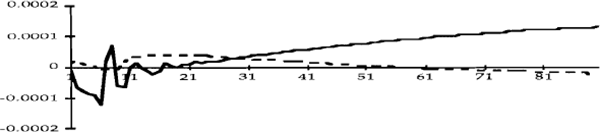
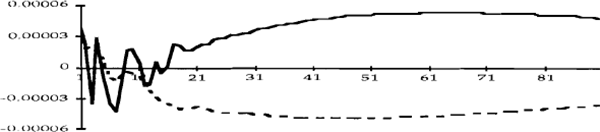
Consider first Figure 2c, which shows the response of the cash rate to an unexpected depreciation of the exchange rate. The impulse responses confirm the hypothesis made in Section 2. In the pre-October 1987 period, an upward shock to the exchange rate (remembering that such a shock is a depreciation of the currency) elicits a prolonged tightening of monetary policy; this policy response is absent in the latter period.
A tightening of U.S. monetary policy (Figure 2a) appears to lead to a tightening of domestic monetary policy, especially after October 1987. We do not, however, infer from this result that shocks to the federal funds rate caused changes in the cash rate, in a structural sense, since at no time during this period did the Reserve Bank's policy reaction for monetary policy ever include a “shadowing” of the federal funds rate. A more plausible explanation is that changes in U.S. monetary policy led to changes in other variables which, over time, led to changes in the cash rate.
This case highlights some of the potential pitfalls of this type of analysis. Notwithstanding the caveats we make in Section 3 (which we consider to be empirically unimportant) we should remember that the VARs are reduced forms, and so the impulse response functions reflect only causality of the Granger type, not structural causality. Our results can, however, be interpreted as being consistent with a certain structural model, for which we might have some priors. For example, Figure 2c is certainly consistent with the notion that monetary policy did in fact react to developments in the foreign exchange rate in the earlier period. On the other hand, the causality that is apparent from the federal funds rate to the cash rate remains something of a structural puzzle.
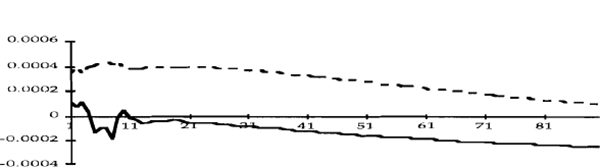
Figure 2e shows that an upward shock to inflationary expectations (i.e. a rise in the Australian bond rate) resulted in a tightening of policy in the pre-October 1987 period, but not afterwards. (One reason for this might be the tendency of this shock to be more sustained in the first period; see Figure 4e.) This result can also be interpreted as indicating that downward shocks to inflationary expectations led to a more substantial easing of monetary policy in the first period than in the second. Shocks to inflationary expectations in the United States, on the other hand do not appear to have had much of an effect on Australian monetary policy.
To summarize, the nature of the Australian monetary policy reaction function appears to have changed in the following way after October 1987. Much less emphasis has been placed on innovations to inflationary expectations, and on developments in the foreign exchange market. Of course, this might simply reflect the fact that there have been no exchange rate “crises” since October 1987 which have necessitated a monetary policy reaction, and we do not rule out such a reaction in the future.
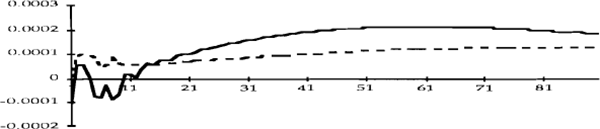
Figures 3a-3e show the impulse responses of the exchange rate. Shocks to U.S. monetary policy appear to have had negligible effects on the exchange rate in the first period; in the second period, the exchange rate appreciates in response to a tightening of policy in the United States, and can therefore be expected to depreciate to its equilibrium value of zero at some future time. This is consistent with the sustained increase in the cash rate that results from this shock since, due to the arbitrage of domestic and foreign asset returns, domestic interest rates will exceed foreign interest rates during this period of adjustment.
Shocks to U.S. inflationary expectations lead to an appreciation of the exchange rate, while tighter monetary policy in Australia leads to a sustained exchange rate appreciation in the pre-October 1987 period and to a somewhat less sustained appreciation in the later period. However, while a cash rate shock has the expected effects in terms of direction, the quantitative effect is very small. On the other hand, a shock to inflationary expectations has a very large effect on the exchange rate, especially post-October 1987.
As a matter of interpretation, we should emphasize that these results do not imply that monetary policy was less responsive, in some sense, to inflationary pressures after October 1987. In fact, the opposite conclusion is warranted. The results are consistent with the following interpretation of events: a downward shock to inflationary expectations is followed by a larger appreciation in the second period than in the first because, after October 1987, this shock did not lead to an easing of monetary policy.
The responses of the bond rate to the various shocks are shown in Figures 4a-4e. What stands out in these figures is the apparent insensitivity of the bond rate to innovations in the other variables. This suggests that inflationary expectations in Australia are deeply entrenched and not much affected – at least in the short term – by surprises in domestic monetary policy or developments in international financial markets.
Finally, we note that 95 per cent confidence intervals indicate that the responses, in each period, of the cash rate to shocks in the exchange rate and Australian bond rate are significantly different from each other. These are calculated using Monte Carlo integration with 1,000 replications. For the thirteen other comparative responses, the confidence intervals indicate that the different responses in each period were not statistically different from each other. These confidence intervals are shown in the Appendix.
c. Variance Decompositions
The information contained in the impulse response functions can be equivalently represented by variance decompositions i.e. the proportion of the variance of the forecast of any variable that is caused by shocks to all of the variables in the system. Generally speaking, the forecast variance of a variable which is essentially exogenous will be largely explicable by the variance of its own innovations. Since there is little feedback to it from the other variables, its forecast variance will be little affected by innovations in the other variables.
Tables 1–3 contain the variance decompositions of the cash rate, the exchange rate and Australian 10 year bond rate, respectively. The information in the tables confirms the inferences that we made from the impulse responses.
| Period 1 (2/1/85 – 20/10/87) | |||||
|---|---|---|---|---|---|
| Day | FF | USB | E | UCR | AB |
| 1 | 0.0 | 0.1 | 0.5 | 99.3 | 0.0 |
| 10 | 0.8 | 2.6 | 2.6 | 92.3 | 1.8 |
| 30 | 9.9 | 4.0 | 11.1 | 65.1 | 9.9 |
| 60 | 10.3 | 3.3 | 18.7 | 49.4 | 18.3 |
| 90 | 9.7 | 3.5 | 21.5 | 45.2 | 20.2 |
| 180 | 9.4 | 5.8 | 21.6 | 43.4 | 19.8 |
| Period 2 (21/10/87 – 30/1/90) | |||||
| Day | FF | USB | E | UCR | AB |
| 1 | 0.0 | 0.1 | 0.0 | 99.9 | 0.0 |
| 10 | 0.8 | 3.4 | 1.6 | 90.4 | 3.8 |
| 30 | 6.7 | 2.3 | 1.5 | 86.2 | 3.5 |
| 60 | 22.9 | 1.6 | 3.0 | 70.1 | 2.4 |
| 90 | 34.9 | 1.5 | 7.6 | 53.9 | 2.0 |
| 180 | 40.2 | 2.2 | 23.3 | 27.1 | 7.2 |
|
FF = federal funds rate, USB = U.S 10 year bond rate, E = $A/$US exchange rate, UCR = unofficial cash rate, AB = Australian 10 year bond rate. |
|||||
| Period 1 (2/1/85 – 20/10/87) | |||||
|---|---|---|---|---|---|
| Day | FF | USB | E | UCR | AB |
| 1 | 0.0 | 0.2 | 99.8 | 0.0 | 0.0 |
| 10 | 0.1 | 1.5 | 95.5 | 0.3 | 2.6 |
| 30 | 0.8 | 3.4 | 90.4 | 2.0 | 3.3 |
| 60 | 0.7 | 3.4 | 89.8 | 3.4 | 2.8 |
| 90 | 0.7 | 3.3 | 89.0 | 3.8 | 3.1 |
| 180 | 0.8 | 3.3 | 87.7 | 3.9 | 4.3 |
| Period 2 (21/10/87 – 30/1/90) | |||||
| Day | FF | USB | E | UCR | AB |
| 1 | 0.5 | 0.2 | 99.3 | 0.0 | 0.0 |
| 10 | 1.0 | 5.9 | 89.2 | 0.4 | 3.5 |
| 30 | 1.9 | 6.4 | 80.4 | 0.3 | 10.9 |
| 60 | 2.9 | 4.3 | 68.8 | 0.3 | 23.7 |
| 90 | 3.2 | 4.0 | 60.3 | 0.2 | 32.3 |
| 180 | 3.1 | 6.2 | 53.1 | 0.2 | 37.4 |
|
FF = federal funds rate, USB = U.S 10 year bond rate, E = $A/$US exchange rate, UCR – unofficial cash rate, AB = Australian 10 year bond rate. |
|||||
| Period 1 (2/1/85 – 20/10/87) | |||||
|---|---|---|---|---|---|
| Day | FF | USB | E | UCR | AB |
| 1 | 0.1 | 0.0 | 16.2 | 0.5 | 83.2 |
| 10 | 0.1 | 0.9 | 17.9 | 0.1 | 81.0 |
| 30 | 0.6 | 1.0 | 21.6 | 0.7 | 76.0 |
| 60 | 0.6 | 2.5 | 25.8 | 1.7 | 69.3 |
| 90 | 0.6 | 4.7 | 26.6 | 2.5 | 65.7 |
| 180 | 1.2 | 8.3 | 25.2 | 2.9 | 62.5 |
| Period 2 (21/10/87 – 30/1/90) | |||||
| Day | FF | USB | E | UCR | AB |
| 1 | 0.0 | 0.8 | 0.6 | 0.1 | 98.6 |
| 10 | 0.7 | 0.6 | 1.3 | 0.1 | 97.3 |
| 30 | 0.4 | 1.6 | 1.1 | 0.1 | 96.7 |
| 60 | 0.9 | 6.3 | 3.7 | 0.4 | 88.7 |
| 90 | 2.3 | 10.0 | 9.1 | 0.6 | 78.0 |
| 180 | 6.5 | 10.2 | 20.8 | 0.7 | 61.7 |
|
FF = federal funds rate, USB = U.S 10 year bond rate, E = $A/$US exchange rate, UCR. = unofficial cash rate, AB = Australian 10 year bond rate. |
|||||
Table 1 shows that innovations to the exchange rate and the Australian bond rate comprise a much larger proportion of the forecast variance of the cash rate in the pre-October 1987 period, especially over shorter time horizons in the case of the exchange rate. After 180 days in the second period, however, the exchangerate accounts for nearly one quarter of the forecast variance in the cash rate, indicating that while short term changes in the exchange rate during this time were less relevant, longer term effects were still important.
Innovations to U.S. monetary policy appear to have become much more important in the later period; after 180 days, they explain 40 per cent of the forecast variation in the cash rate. However, it is interesting to note that, in the short run, the federal funds rate explains very little of the forecast variance in the cash rate, which is consistent with our prior view that no structural causality runs from the federal funds rate to the cash rate.
Table 2 confirms that unexpected changes in monetary policy appear to have had little effect, in either period, on the exchange rate. However, innovations to the Australian bond rate (inflationary expectations) do seem to have had a significant effect on the path of the exchange rate after October 1987, consistent with the result that such shocks have not had a particularly large effect on the cash rate during this time.
Table 3 confirms our earlier conclusion that inflationary expectations in Australia seem to be very difficult to move. Even after 180 days (in both periods), over 60 percent of the forecast variance of the bond rate is explained by its own innovations. Innovations to the cash rate, however, have only a negligible effect. Exchange rate shocks appear to have had a significant effect on inflationary expectations the first period but not so much in the second period, except after 180 days. Innovations to inflationary expectations in the U.S. also seem to be of some significance, especially at longer time horizons.
Footnotes
This, of course, was the date of the stock-market crash. We are emphatically not saying that the crash was the cause of any structural break, particularly in the monetary policy reaction function. What is likely, however, is that the post-crash depreciation of the exchange rate was the first occasion in which such a depreciation did not lead to a policy-induced increase in interest rates. [8]
In the case of the exchange rate, the responses are for the natural logarithm of the exchange rate. [9]
