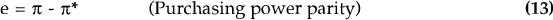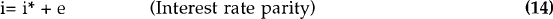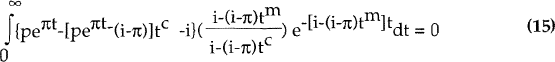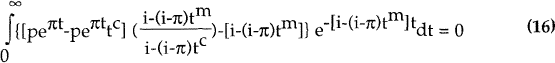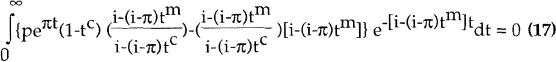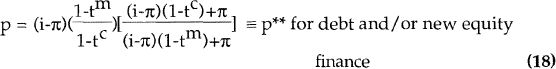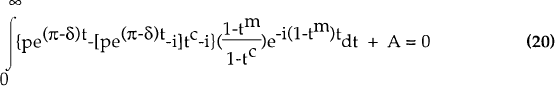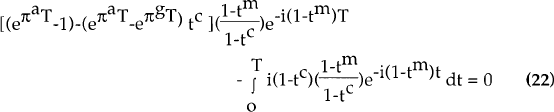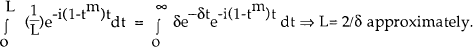RDP 9011: Inflation and Corporate Taxation in Australia 4. The Effects of Inflation

This section discusses four distorting effects of inflation on corporate activity. Each occurs despite the presence of imputation. Uncertainty is ignored so as to focus on inflation's interaction with the tax system.

(i) Inflation and Interest Rates

The above analysis has taken the nominal interest rate as given, and has shown that a necessary condition for inflation to be neutral in its impact on investment is that the real after-tax interest rate is invariant to inflation. If this condition were satisfied, and inflation had no other distorting effects on the system, then the fact that the tax treatment of interest is based on nominal rather than real rates would not distort investment decisions. Nominal interest rates could simply rise to maintain the equilibrium real after-tax interest rate.

The following argument suggests that this kind of distortion-free outcome is in fact not possible. Consider an economic system which includes the following two equilibrium conditions:

where e is the rate of change of the nominal exchange rate, and the asterisk denotes a foreign variable. Suppose we start from an equilibrium with π = π^* and the domestic (real) interest rate equal to the world (real) interest rate. If the domestic inflation rate then rises (by Δπ), it is impossible for the above two conditions to be satisfied simultaneously with a constant real after-tax interest rate. There must be either a reduction in the domestic real after-tax interest rate (of t^mΔπ), or a real exchange rate appreciation, or some combination of the two.

It is often argued that such distortions can be overcome by moving to a tax system based on real, rather than nominal, interest receipts and payments. Appropriate modification of the intertemporal model shows this is not quite true. In fact, unless t^m equals t^c it is not possible to have a tax system which corrects this problem and at the same time is neutral with respect to the choice between debt and equity financing. The reason for this is that the benefit to lenders arising from tax indexation of interest receipts would be πt^m whereas the direct cost to firms of tax indexation of interest payments would be πt^c.

To demonstrate these results rigorously, we can rewrite the marginality condition using an imputation factor of [i−(i−π)t^m]/[i−(i−π)t^c] rather than (1−t^m)/(1−t^c).^[8]

The marginal conditions are then found by rewriting (2) (debt), (4) (new equity) and (5) (retained earnings) as:

The solutions for the required real rate of EBIT are:

and:

These solutions show that indexation of interest, combined with an appropriately modified imputation system, would be ideal if t^c equalled t^m. If so, the marginal condition would be that the real earnings rate must equal the real interest rate regardless of the inflation rate or the source of funds. And neutrality of inflation with respect to its effect on the level of investment would be preserved by maintaining real pre-tax interest rates rather than real after-tax interest rates as required under the non-indexed system. This would solve the problems referred to earlier whereby inflation distorts real after-tax interest rates and/or the real exchange rate.

It should be noted in concluding this sub-section that provided t^m is sufficiently close to t^c, these ideal results would at least hold as an approximation. A rise in inflation which results in an equal rise in nominal interest rates would have a relatively small effect on investment. (If t^m exceeds t^c, the effect would be positive because the benefit to lenders would exceed the cost to borrowers. The reverse would hold if t^c exceeds t^m.) Thus indexation would be likely to substantially reduce the distortions associated with a nominal-interest tax base, even if they were not entirely eliminated.

(ii) Inflation and Capital Depreciation

A widely recognised problem with the corporate taxation system is that depreciation allowances are based on historical cost rather than replacement cost. With positive inflation, this usually means that the real value of depreciation allowances understates true depreciation, with the degree of understatement being larger the longer the lifetime of the asset (and the higher the inflation rate)^[9]. It is often concluded from this argument that there is a tax bias away from assets with long lifetimes. This is true up to a point but for assets with very long lifetimes (very low rates of depreciation) this bias must become economically unimportant as depreciation itself becomes a relatively unimportant factor in the investment decision.

To see these points in the context of the model developed so far, consider an asset which depreciates at a rate δ, and hence has nominal earnings growth of (π−δ) rather than π. Defining the present value to shareholders of depreciation allowances as A,^[10] the solution to the required (initial) real rate of EBIT is given by rewriting equation (2) as:

The first term in (21) reflects the inherent economic advantage of assets whose rate of depreciation (δ) is low. The second term reflects the tax bias towards rapidly depreciating assets (A high).

Figure 3 plots the solution to equation (21) against the asset's half life given an inflation-nominal interest rate combination of 7% and about 15% respectively.^[11] The economic advantage of low depreciation always outweighs the tax bias because of the distinction between historical and replacement cost and the fact that any tax deduction only compensates the firm at the rate of tax. Thus the required real rate of earnings falls with asset longevity.

As noted above, one may think that for given real after-tax interest rates, slowly depreciating assets suffer the most from inflation; the gap between historical and replacement cost widens most and distant deductions are particularly heavily discounted. But the viability of an asset which does not depreciate at all is obviously unaffected by distortions to the real value of depreciation allowances. At the other extreme, an asset which depreciates immediately is similarly unaffected by such effects of inflation. This suggests that the distortion arising from the interaction of inflation and depreciation is least for assets with either extremely short or extremely long lifetimes: inflation has its most deleterious effects on assets which depreciate at a moderate rate.

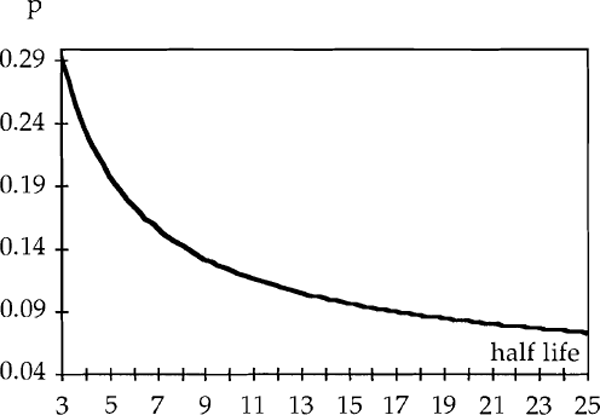
Figure 4 shows that, strictly speaking, this is true. It shows the ratio of required real pre-depreciation rates of return, assuming inflation rates of 7 and 4 per cent respectively. (So as to focus on the depreciation distortion, it is assumed that inflation does not erode the real after-tax interest rate – a constant 2% – and, as in Figure 3, that corporate and personal tax rates are equal.) Two important conclusions emerge from this graph. First, the interaction of inflation and depreciation always penalises investment (ie requires a higher real, pre-depreciation return), whatever the depreciation rate of the asset involved. Secondly, this penalty is greatest for assets of medium life. The exact definition of medium will depend on the parameters of the tax system – in the above calculations, medium is a half-life around 6–12 years.

Realistically, most plant and equipment has a half-life of less than 6–12 years. Consequently, it is fair to focus on the rising part of the curve and conclude that increases in inflation make one less inclined to invest in fairly slowly depreciating plant and equipment than otherwise. In fact, this assertion is quite conservative. Equation (21) shows that, with real after-tax rates assumed constant, Figure 4 depends only on the depreciation allowances. Moreover, this is true whether economic depreciation is exponential or straight-line. Assuming straight line allowances, rather than their approximation as used above, shows that the peak is still 1.06 and it occurs at an assessed life of 24 years. This is beyond the assessed life of virtually all plant and equipment.^[12] On the other hand, buildings clearly have lives well in excess of this, and probably fall in the part of the curve where relative bias is reduced as the asset life is lengthened. Furthermore, buildings probably benefit more from the subject of the next sub-section than do plant and equipment.

(iii) Inflation and Capital Gains

Prior to the introduction of capital gains tax in 1985, the tax system gave a clear advantage to assets which yielded their income in the form of capital gains. Capital gains taxation has in large part removed this advantage but, because the tax is levied only on the real component of capital gains, they remain more favourably treated than other forms of income which are assessed on a nominal basis. Quite apart from issues of tax avoidance associated with the artificial conversion of income into capital gains, this treatment of capital gains will tend to encourage the allocation of investment towards the kind of assets which appreciate in value, relative to assets which yield a stream of income.

To take the most extreme comparison, suppose a firm can invest one dollar in an asset which produces no income at all but rises in value because it is expected to produce income in the future. If the nominal value of this asset is inflating at rate π^a, as distinct to general inflation of π^g, then shareholders will be indifferent to purchasing the asset and holding it for T periods if π^a is such that:

The first term represents the present value of the net return to shareholders after the asset has been sold, the loan repaid, and tax paid on the real capital gain. The second term represents the net cost of interim interest payments (note that interim tax is – it^c each period).

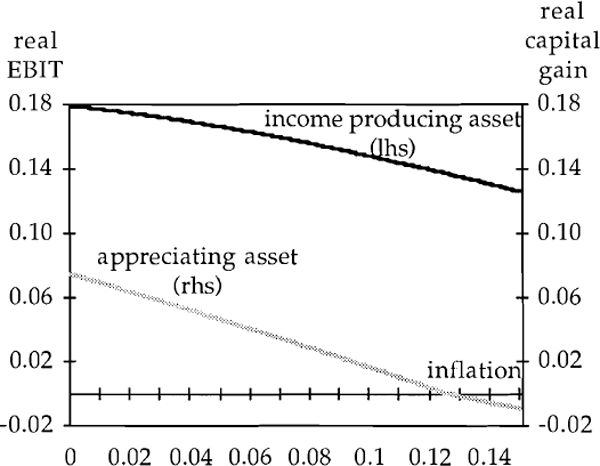
Figure 5 focuses on the distinction between the treatment of this asset and a depreciating income-producing asset by assuming real after-tax interest rates are not eroded by inflation and that t^m = t^c. If the asset is intended to be held for five years, then its purchase is viable if it appreciates at a real rate of 3.2% per annum, regardless of the inflation rate. On the other hand, the depreciating income-producing asset must earn an initial real rate of EBIT of around 15–16% at current inflation rates. Its feasibility falls as inflation rises because of the reduced real value of depreciation allowances.

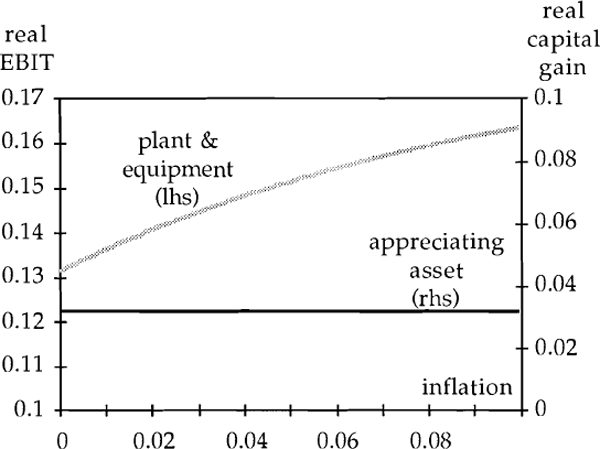
If changes in inflation erode real after-tax interest rates, the incentive to acquire appreciating assets rather than depreciating income-producing assets is even greater: because of the failure of interest rates to fully adjust to inflation, the lack of income in the interim is less costly. Figure 6 illustrates this. Falls in the required real rate of appreciation are proportionately much greater than falls in the required (initial) real rate of EBIT.^[13]

The immediate effect of the tax incentives to purchase appreciating assets is to raise the price of the existing stock of such assets. As π^a rises above π^g and is expected to continue rising, the incentive becomes even greater. As shown in Section 3(iii), those who are confident they can buy and sell at a substantial profit may well prefer to fund their speculation with debt rather than equity, even post-imputation. This argument was even stronger for most of the 1980s. Macfarlane (1989) argued that it was a major influence on the rise in debt over the 1980s.

Of course, the major difficulty with asset speculation is that it does not generate steady cash flow. However, the next sub-section shows that even investment in an asset which produces a steady stream of real earnings (and no capital gain), over a period of stable interest rates and inflation, can cause cash flow problems.

(iv) Inflation and Cash Flow

As noted earlier, inflation generally involves deferral of the cash flow on an investment. If inflation is higher than the depreciation rate, the typical pattern is one of losses in early periods which, in present value terms, are matched by gains in later periods. These losses and gains are exacerbated by inflation. In the absence of credit rationing or liquidity constraints, such a cash flow pattern is not regarded in the academic literature as a problem, since any cash needs could be met by borrowing. But this is unrealistic as a practical proposition and the deferral of cash flow tends to reduce the incentive to invest, particularly for assets with long lifetimes.

The implied pay-back periods can be surprisingly long. Suppose inflation is 7%, the nominal interest rate is about 15% and the asset depreciates very slowly, having a half life of about 17 years. Figure 7 shows the time path of the discounted net return to shareholders assuming that the project is marginal in terms of net present value. (The step down reflects an assumption of straight line depreciation allowances for 20 years, implying relatively rapid deductions and hence a smaller deficit at first than otherwise.) Clearly, it takes a long time for gross earnings to exceed tax and interest obligations.

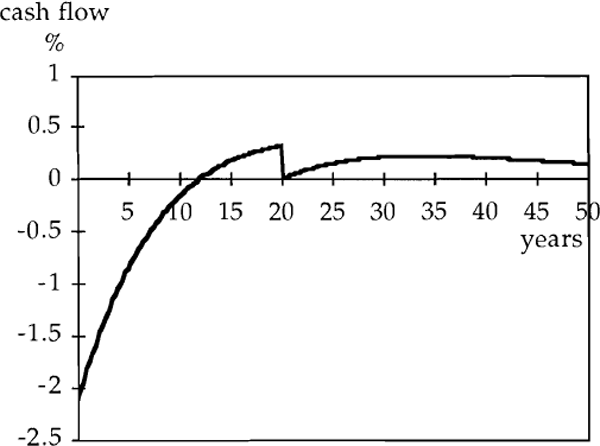
Indexation of the tax treatment of interest receipts and payments in the manner discussed earlier would not solve this problem as earnings would still inflate while interest costs were constant. Indexation of the capital component in loan agreements would solve the problem but their use does not appear to be widespread.^[14]

Footnotes

Cost of equity = cost of debt <=> dividend paid = i−(i−π)t^c

Return on equity = return on interest <=> net dividend received = i−(i−π)t^m 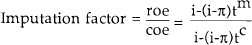[8]

There have been offsetting influences arising from various accelerated depreciation provisions and investment allowances. These are discussed in detail by Willmann (1990), who notes that in some cases these more than fully compensated for inflation. However, this does not negate the basic point made in this section that, because the depreciation rules are based on historical cost, a rise in inflation always reduces the attractiveness of an investment. [9]

Suppose that, although economic depreciation is exponential, the Tax Office has chosen a statutory lifetime (L) which implies that deductions of (1/L) for each of L years have the same present value as would exponentially declining deductions. (Hence both present values fall short of the actual historical cost, let alone the replacement cost.)

View MathML

i.e. 1/L for each of L periods is equivalent to exponentially declining deductions beginning with 2/L. (See King and Fullerton (1984) for a similar approximation.) Note that this equivalence does not contradict the Tax Office's actual alternative of linear diminishing value deductions beginning with 1.5/L.

Reflecting the May 1988 decision concerning investment in plant and equipment, the firm is then allowed to deduct (1.2/L) for each of (L/1.2) years, thereby raising the present value of what shareholders receive to an amount defined as A:

View MathML

[10]

The half life is the time taken for the asset to lose half its real value under exponential depreciation. This is given by (ε^−δt = 1/2⇒ t=(ln2)/δ). The inflation, nominal interest rate combination was chosen so that if t^m = t^c = .39, the real after-tax interest rate is 2% = .1475 (1−.39) −.07. [11]

Figure 4 suggests the effect of inflation is relatively small; interpreting the curve as the ratio of the two present values of all future gross earnings (discounted equally at the social discount factor) implies a distortion which peaks at 6%. Nevertheless, Freebairn (1990) also concluded there is a bias away from middle-lived assets. Willmann (1990) quantified the adverse effect of inflation on taxable corporate income due to the tax treatment of depreciation and concluded there is a bias towards short-lived assets. That result is due to separating the effects of inflation and depreciation on the present discounted values of allowances. [12]

Nominal interest rates are assumed to be always 8 percentage points above the inflation rate which, for t^m =.39, implies real after-tax interest rates of about .05−.39π.

The treatment of capital gains is asymmetrical; an asset's value must fall below its actual purchase price before a deduction is granted. For the purposes of Figure 6, equation (22) has been modified accordingly (0<π^a<π^g⇒ the term for capital gains tax is dropped). The effect is to make the grey line fall a little less rapidly after it crosses the x-axis. Note that if the asset held for capital gain produced any income during the holding period, its attractiveness would be even greater. [13]

It should be noted than when an asset is depreciating more rapidly than inflation, the typical cash flow pattern is reversed, with early profits being followed by losses. To be of marginal worth, the rapidly depreciating asset must earn high nominal returns early, before its gross income-earning capacity is eroded by depreciation. [14]