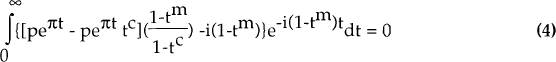RDP 9011: Inflation and Corporate Taxation in Australia 3. The Level of Investment and the Choice of Funds

(i) Imputation

A simple exposition suggests that full imputation has eliminated the basic source of tax bias towards debt. Under full imputation, the payment of a dividend of d implies an imputation credit of dt^c/(1−t^c), where t^c is the corporate tax rate. Personal tax is levied on the sum of these two amounts at rate t^m, and total tax payable is then reduced by the amount of the credit. This results in a net dividend (after personal tax) of:

The net dividend is equivalent to the amount that would be received if corporations paid no tax at all, with dividends then being subject to the normal laws of personal income taxation. This equivalence can be seen by noting that if there were no corporate taxation, all earnings after interest could be distributed, rather than a fraction (1−t^c) of that amount. Hence, d/(1−t^c) would be received which, after personal taxation, leaves the amount derived above.^[2]

For a given dividend payment, imputation has increased the net dividend received. The obverse of this is that imputation has increased the cost to shareholders of a reduction in dividends payable. Consequently, the cost to shareholders of debt repayments has risen. In fact, it now equals the cost of equity finance. To see this, suppose the firm uses one dollar of debt to finance an investment. The tax deductibility of interest payments means this debt reduces dividends payable by i(1−t^c) dollars only. Prior to imputation, this would have cost shareholders i(1−t^c)(1−t^m) dollars only. Equation (1) shows that it now costs shareholders i(1−t^m) dollars. But this would be the (opportunity) cost to shareholders of providing the dollar themselves. Hence, shareholders are indifferent between debt and equity. Moreover, this result is not directly affected by inflation: the net cost to shareholders of either type of finance is i(1−t^m), regardless of i.

(ii) An Intertemporal Model of Investment and its Funding

It will be useful to formalise the above exposition in a fully intertemporal model, which can then be used to address a broader range of questions. This can be done along the lines proposed by King and Fullerton (1984) in a prominent contribution to the literature on tax biases in corporate finance. King and Fullerton proposed two methods to calculate the percentage difference between the real pretax rate of return on the marginal investment and the real after-tax interest rate. If this difference, known as the effective tax rate, is independent of the source of finance, the tax system is said to be neutral with respect to the financing decision.

In their “fixed-p” method, the real pre-tax return on the firm's investment (p) is assumed to be exogenous. One then solves for the real after-tax interest rate (s) which would imply the investment is of marginal worth. The problem with this method is that the resultant s can differ according to the type of finance used (and, by definition, does so whenever the system is non-neutral). Consequently, it can imply that companies face different real interest rates when they invest in equivalent projects but with different types of funds.

The alternative “fixed-r” method assumes the real interest rate is exogenous and common to everyone, but implies that p can differ according to the means of finance. This begs the question of why the firm ever uses more than one source of funds, i.e. whichever source results in the lowest p. For example, under the classical tax system, with no imputation, the original shareholder in a company would always prefer debt. However, this problem can be overcome by introducing uncertainty into the model. The fixed-r method also allows one to make explicit assumptions about overseas influences on domestic interest rates. Finally, it allows a more straightforward analysis of the effects of the tax system on the allocation of investment, i.e., examining how the tax system affects the required rate of return on a particular type of investment, given the cost of funds. Hence, it is this method which is adopted in the present paper.^[3]

The version of the fixed-r model presented below reflects Scott's (1987) criticism of King and Fullerton's fixed-r model. Scott argued that, assuming the firm's objective is to maximise the present value of all net payments to existing shareholders, the marginal project is that for which the present value of the cost of the project to existing shareholders equals the present value of the benefit of the project to those shareholders. Hence the appropriate discount factor is the shareholder's opportunity cost – i(1−t^m) – regardless of the means of financing the project.

Assuming full imputation and ignoring depreciation, three financing options (debt, equity and retained earnings) can be considered.

(a) Debt finance: The firm borrows and invests one dollar and every period distributes all that it can to existing shareholders.

The investment yields a constant real rate of earnings before interest and tax (EBIT) of p, which in nominal terms inflates at rate π.

Imputation implies the net dividend to shareholders is [(1−t^m)/(1−t^c)] × 100% of whatever is left after the firm pays tax and interest. Shareholders are indifferent between the investment going ahead or not when p is such that the net present value of cash flows from the investment is zero:

which implies:

This condition simply states that the real rate of earnings before interest and taxes must equal a certain multiple of the real after-tax interest rate. This has two interesting consequences. First, inflation can only be neutral for the level of investment if it does not affect real after-tax rates of interest; and secondly, when inflation is positive, marginal investments will always yield negative initial cash flows (compensated by positive cash flows in later periods).^[4]

(b) Equity finance: The firm finances the investment by issuing one dollar of equity to existing shareholders and again distributes all that it can in each period.

In this case, there are no repayments of interest and no interest deductions from tax. The shareholders, by using either savings or a tax deductible loan, incur a cost of i(1−t^m) each period on the dollar they provide to the firm. Hence shareholder indifference requires p to be such that:

The left hand side of (4) can be rearranged to be identical to the left hand side of (2), implying that the marginal investment is the same as with debt, and must therefore also earn a return of p^*. In other words, the required rate of return on investment is unaffected by whether it is funded by debt or equity. The intuition is exactly the same as in the simple exposition: the net cost to shareholders of either type of fund is i(1−t^m) each period.

(c) Retained earnings: The firm finances the investment by retaining one dollar of earnings from previous investments.

It might seem that because retained earnings represent a form of equity financing, the results for this case should be the same as those applying to the issue of new equity. This is not strictly correct. Consider a firm which distributes profits and then immediately raises an equivalent amount by issuing equity. The shareholders will not be indifferent between this and simply retaining the profit from the start, unless the personal and corporate tax rates are equal; the direction of preference will depend on which tax rate is the larger.

More formally, we can note that at any time period t in the future, a dollar of retained earnings generates dollars for the shareholders. However, the dollar deprived shareholders of (1−t^m)/(1−t^c) dollars, which would have returned dollars in each future period if invested at interest.

Hence the marginal investment is such that:

which implies:

When financed out of retained earnings, the required rate of return on an investment relative to p^* thus depends on the relative sizes of the personal and corporate tax rates. This reflects the fact that shareholders sacrifice one dollar to provide new equity and (1−t^m)/(1−t^c) dollars to forego dividends and “provide” retained earnings. If t^m exceeds t^c, the required return on the firm's investment is lower than for the other forms of finance, and hence the tax system can be said to favour retained earnings. If t^m is less than t^c, the reverse is true. Which of these cases holds at the margin is in fact not obvious. Although the top marginal tax rate exceeds the corporate tax rate under the present system, a great deal of personal investment is conducted through superannuation funds, which enable individuals to attain lower marginal tax rates for their investments.^[5]

(iii) Can there still be optimal leverage and how would it have changed with imputation?

The exposition of the previous sub-section ignored the distinction between issuing equity to existing shareholders or new shareholders. This was made possible by the assumption that all investments break even: existing shareholders were not concerned with the prospect of diluted profits or concentrated losses.^[6] Dropping this assumption does not affect the neutrality result if existing shareholders are capable of providing new equity (either by drawing on savings or making tax deductible loans). To see this, suppose a firm could borrow $10 from the bank or $1 from each of its existing ten shareholders. In either case, the net present value of returns to each shareholder is (p/p^*)−1 (from the general solutions to equations (2) and (4)). As before, the reason is that the cost of either type of fund is i(1−t^m).

If existing shareholders are incapable of providing new equity and it must be issued to outsiders, the fact that investments do not always break even means that, despite imputation, risk-return considerations continue to apply to the firm's funding decision. The higher the leverage of a firm, the greater the mean and variance of returns accruing to shareholders. If creditors bear none of the burden of variations in EBIT and shareholders are small in number, each shareholder has to bear a relatively large part of the burden of changes in the rate of EBIT. If the shareholders are risk averse, there will be some degree of leverage which optimises the risk-return tradeoff.

To see this, suppose the firm's investments yield a stochastic real rate of EBIT (p) with expected value ε(p) and variance σ². The net present value to each of E shareholders of a one dollar investment in a company with debt of D is given by:

and has a distribution characterised by:

where for our purposes, Z can be regarded as exogenous.

The optimal degree of leverage is then determined by maximising, with respect to D/E:

where R is the coefficient of relative risk aversion. The result is:

If the investment were certain to break even (ε(p)=p^*, σ²=0) the right hand side of equation (11) would be undefined. This is consistent with the result that shareholders would not care what leverage was adopted. If the investment were only expected to break even (ε(p)=p^*, σ²>0) the right hand side of equation (11) would equal −1: shareholders would cancel their risk by insisting the firm invest all equity in an interest-bearing asset. This reflects the fact that ε(p) must exceed p^* to compensate for risk.

In general, however, the optimal degree of leverage is an increasing function of:

• higher expected rates of return (ε(p));
• lower real after-tax interest rates (and hence lower p^*);
• reduced risk aversion (R); and
• reduced volatility of returns (σ²).

Equation (11) can be contrasted with the classical tax system, in which (1−t^m)/(1−t^c) is replaced by (1−t^m). In this case, optimal leverage – (D/E)^cl – can be expressed as:

which is clearly much greater than the post-imputation optimum.^[7]

The main conclusions to be drawn from this section are:

• there is no longer a direct tax bias towards debt and away from equity;
• there is a relatively minor tax distortion between debt and equity on the one hand and retained earnings on the other; and
• for reasons other than imputation, an optimal debt equity ratio may still exist but this ratio would be considerably less than the optimum prior to imputation.

Footnotes

In the absence of corporate taxation, d could be (p−i) where p and i denote earnings before interest and tax (EBIT) and interest repayments respectively. In the presence of taxation d is limited by p−(p−i)t^c−i=(p−i)(1−t^c).

Note that personal tax 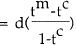. Hence, if t^m is less than t^c the “correct” amount of tax is negative, which is not allowed. To overcome this, the credit can be offset against any income. [2]

The BIE (1990) adopted King and Fullerton's fixed-p method. While aware of the relative merits of each model (which it referred to in its Appendix B) the Bureau considered the fixed-p method more suitable for its purposes. Nonetheless, the Bureau's conclusions concerning the funding decision were broadly in line with those of this paper. [3]

This explains why p^* is independent of the degree of imputation; partial imputation would reduce the early losses as well as the latter gains. However, the present value of all returns from an investment which earned more (or less) than p^* each period would be linear in the degree of imputation. Furthermore, the degree of imputation affects the marginal condition for equity financing. [4]

There are two assumptions in the above analysis which require explanation. The first is that no earnings are retained once an investment, however funded, is underway. The retention of subsequent earnings would represent a new investment decision but the general conclusions concerning debt and equity versus retained earnings would be unaltered because this new decision would be based on the same principles as the initial decision.

The second (apparent) assumption is the irrelevance of capital gains tax on equity. Given all investments are assumed to break even, there are no capital gains or losses. Altering the model so that a retained dollar is assumed to be invested in debt or new equity's marginal investment shows that the decision to use retained earnings or external finance still depends on the relative magnitudes of t^m and t^c: substituting p^* into (5) implies a net benefit (loss) of (t^m−t^c)/(1−t^c).

[5]

The present value of the dividend paid to new shareholders must be such that they are indifferent between buying shares or an interest bearing asset. Hence the amount existing shareholders are deprived of – the payment to new shareholders – is the same as what existing shareholders are deprived of if they buy the shares themselves. Formally:

View MathML

and

View MathML

which combine to reproduce (4) i.e. the critical value for p is again p^*.

[6]

An alternative demonstration of the impact of imputation is its impact on the expected market value of the firm:

ε(mvf) = D+E(ε(q)+1) = (ε(p)/p^*)(D+E)

Under imputation, transfers between debt and equity have no effect on the expected market value of aggregate equity and debt. (The original Modigliani-Miller (1958) theorem concerning the value of the firm was based on the same intuition. Their arbitrage explanation is essentially the same as the assumption that the opportunity costs to shareholders of debt and equity are equal.) Under the classical system, however, the value of the firm could be increased by substituting debt for equity:

ε(mvf^cl) = D+E(ε(q)+1)(1−t^c) = (ε(p)/p^*)(D+E)(1−t^c) + Dt^c [7]