RDP 9103: The Failure of Uncovered Interest Parity: Is it Near-Rationality in the Foreign Exchange Market? 3. Discussion

The focus of this paper is on the expected utility costs of sub-optimal strategies rather than on ex post outcomes. For periods as long as a year or more, the ex post returns from the near-rational strategies we consider are sometimes higher than the returns from the fully-optimal strategy. The following simple argument demonstrates why. Imagine a portfolio restricted to assets in the US and a single foreign country and assume that the expected excess real return in the foreign country is 3%p.a.^[8] With ρ = 2, and our empirical estimate of the variance of real weekly excess returns sourced in a foreign country from Table 1 of about 0.0003, a mean-variance optimizing investor will put all of her portfolio in the foreign country.^[9] We now compare the return from this optimal strategy with the return from the sub-optimal “stay-at-home” strategy of keeping the whole portfolio in the US. By straightforward calculation using equation (3), the expected utility cost of this stay-at-home strategy is about 1.5%p.a.

Over a year, the standard deviation of real returns sourced in the foreign country is about 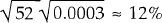, while, by assumption, the expected excess return is 3%. Over a year, exchange rate shocks are approximately normally distributed (Baillie and Bollerslev, 1989). Hence, the probability that, in a randomly chosen year, the stay-at-home strategy will produce a higher ex post real return than the optimal strategy is about Pr(z >¼) where z is a standard normal variable, or about 0.4.

Thus, judged by the expected utility derived from it, the stay-at-home strategy is very costly (with an expected utility cost of about 1.5%p.a. compared, for example, with the cost associated with optimizing portfolio shares every three months in our six-currency model of about 0.16%p.a.). Yet, in a randomly chosen year, the stay-at-home strategy outperforms the optimal strategy about 40% of the time. Even over a five-year period, the stay-at-home strategy outperforms the optimal strategy about 29% of the time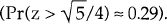

This simple example demonstrates an important point. Even using five years of data, it is very difficult to distinguish between optimal and near-rational strategies using ex post outcomes.^[10] If investors choose to invest their funds with the portfolio manager who has the best performance in, say, the last five years, those managers who engage in near-rational behaviour (e.g., those who optimize their portfolio every three months) will often be chosen as the best performers. Hence, they will not disappear from the market.

The standard test of uncovered interest rate parity is to run the regression

where Δs_t+τ is the change in the log of the spot domestic price of foreign exchange over τ periods, 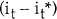is the current interest differential between τ-period domestic and foreign nominal assets and η_t+τ is an error term. Uncovered interest parity holds if β = 1 in the true model (α = 0 is sometimes also included as part of the hypothesis). The overwhelming empirical finding is that β < 1, and often that β < 0. To give a representative example, Goodhart (1988) estimates equation (9) for nine data sets. In six cases out of nine, the point estimate for β is negative, and in five cases out of nine, the estimate of β is more than two standard errors less than one. By contrast, in no case is β significantly greater than one.

Almost without exception, empirical rejections of uncovered interest parity use short-term nominal interest differentials in equation (9).^[11] For example, in the nine tests of uncovered interest parity reported above, six use one month interest rates while the rest use three month interest rates.

Provided some nominal interest rate changes are also real interest rate changes, sluggish adjustment of portfolio shares provides a potential explanation for the failure of uncovered interest parity. Most exchange rate models (Dornbusch (1976) being the most famous example) predict that, other things equal, an increase in domestic real interest rates leads to an instantaneous appreciation of the domestic exchange rate. With a substantial proportion of investors adjusting sluggishly to changes in interest rate differentials, only part of this appreciation occurs immediately, with the rest occurring over a time scale comparable to the time between portfolio adjustments. Then, on average, the short-term interest differential will over-predict the subsequent change in the exchange rate, i.e., (β < 1. Thus, sluggish adjustment of portfolio shares also provides a potential explanation for the direction of failure of uncovered interest parity.

The contribution of this paper is to demonstrate that, in terms of expected utility, the cost of sluggish adjustment of portfolio shares over times relevant to tests of uncovered interest parity is very small indeed. The final step in the argument can then take two possible forms. Either, one can appeal to small transactions or opportunity costs of frequent optimization and argue that sluggish adjustment of portfolio shares is fully optimal. Alternatively, one can argue that, although not fully optimal, sluggish portfolio adjustment costs so little that agents who engage in this behaviour will not be driven from the market.

There are several refinements which could be introduced into our model. Firstly, the conditional variance-covariance matrix for weekly nominal exchange rate changes is more accurately modelled as a GARCH(1,1) process rather than as a time-invariant matrix (Baillie and Bollerslev, 1989) and a similar representation should also be a more accurate model of real excess returns (because the variation in these returns is dominated by nominal exchange rate changes). If Ω follows a GARCH process, there will be some times when the cost of near-rationality is underestimated by our simpler model and other times when it is overestimated. Nevertheless, by an argument similar to Frankel (1988), our model should give a good estimate of the cost of near-rationality averaged over a few months or longer.

Secondly, rather than using equation (2), an alternative modelling strategy would have been to follow Frankel and Meese (1987), and assume that each real exchange rate follows an AR(1) process. Using annual data on the real US/UK exchange rate during the floating period 1973–1984, Frankel and Meese derive point estimates for the autoregressive coefficient of 0.720, and for the mean absolute deviation of the real exchange rate of 0.121. Using this model would introduce a correction to equation (2) with an average magnitude of about (0.121) (1 – 0.720) = 0.034 or 3.4%p.a. While this is a substantial correction, provided this underlying model was known to both the rational and near-rational investors, it is not clear how much difference this refinement would make to the results.

Finally, the analysis is clearly partial equilibrium in nature. There is no examination of how the actions of the representative portfolio investors influence the behaviour of the exchange rates. We intend to examine this link in future research.

Footnotes

This is a substantial expected excess return. In our model framework, it would occur when the short-term differential between foreign and domestic interest rates is 3%p.a. larger than the long-term differential. [8]

Application of equation (4) gives x_t = (0.0006)⁻¹. 0.03/52 ≈ 1. [9]

It is for this reason that we focus instead on expected utility as a measure of the sub-optimality of the strategies we consider. [10]

By contrast, interest differentials on longer-term nominal assets provide a much better guide to longer-term changes in exchange rates. Countries with relatively high inflation have relatively high long-term nominal interest rates and their currencies tend to secularly depreciate against the currencies of low inflation countries. Thus, the failure of uncovered interest parity is a failure of the exchange rate to move as predicted in the short-term but not in the longer-term. Froot and Thaler (1990) make a similar point. [11]