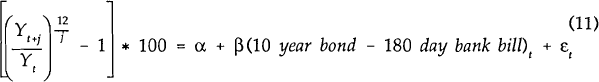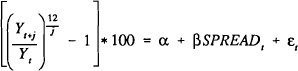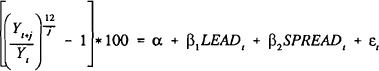RDP 9204: The Term Structure of Interest Rates, Real Activity and Inflation 3. The Yield Curve and Real Activity
May 1992
- Download the Paper 439KB
3.1 Estimation Procedure and Data.
To examine the ability of the slope of the yield curve to predict real activity, both monthly and quarterly data on a number of real activity variables are used. The quarterly data are taken from the Australian National Accounts and include data on GDP, aggregate consumption and aggregate investment. All data are in constant dollars and have been seasonally adjusted. Monthly indicators of real activity include the number of car registrations, the number of dwelling approvals and the Melbourne Institute Index of Industrial Production. This monthly data, as well as all interest rate data, are taken from the Reserve Bank of Australia Bulletin. The sample period runs from September 1972 to June 1991. Further details of the data are available in Appendix 1.
The approach of Estrella and Hardouvelis (1991) forms the basis of the forecasting tests. Their technique involves regressing future changes in real activity on the current slope of the yield curve. Specifically, the following equation is estimated for various forecast horizons:
where γt, is the value of the forecast variable at time t and j is the forecast horizon in terms of the number of months. The spread between the 10 year Treasury bond rate and the 180 day bank bill rate is used as the measure of the slope of the yield curve[3]. Various other spreads were also examined for their information content and selected results for GDP are reported in Appendix 3.
In all but the one period forecasting regressions, the sampling interval is longer than the forecast horizon. The overlapping observations induce a moving average process of order j−1 into the residuals making the estimated standard errors inconsistent. To make the standard errors robust with respect to both this induced serial correlation and to any remaining serial correlation the Newey-West (1988) estimator of the covariance matrix is used with the number of lags equal to j+2. This covariance estimator also makes the standard errors robust to conditional heteroskedasticity. The actual coefficient estimates are calculated by Ordinary Least Squares.
3.2 Results.
In July 1982 the authorities moved from a tap to a tender system for issuing government bonds[4]. Under the tap system the interest rate was set by the authorities who then supplied the government bonds demanded at that rate. Under the tender system, the government determined the supply and the interest rate was determined in the market. While both systems can theoretically generate the same outcome, interest rates under the tender system have tended to reflect market conditions and expectations more accurately than was the case under the tap system. Graph 1 shows the yield spread between the 10 year Treasury bond rate and the 180 day bill rate over the period of study. It shows that the period prior to the scrapping of the tap system was characterised by a much more stable spread than the more recent period. The one obvious exception is in 1974 when extremely tight credit conditions caused the absolute value of the spread to increase to over ten percent for a short period of time. It might well be expected that the movement from rates being set by the authorities to being set directly in the market would alter the relationship between the yield curve and future output changes.
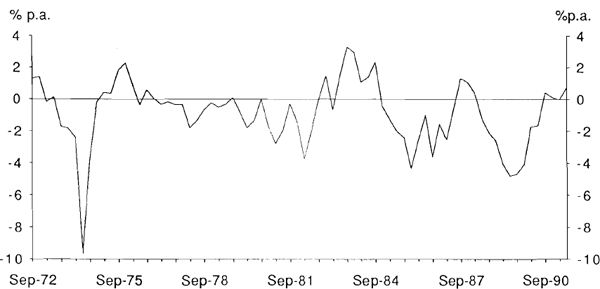
Given the change in operating procedures, the sample period is split into two periods. The first running from September 1972 to June 1982 and the second from September 1982 to June 1991. Tables 1 and 2 report the estimation results of equation (11) for the two periods using the quarterly National Accounts data.
| GDP | CONSUMPTION | INVESTMENT | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| j | α | β | 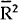 |
α | β | 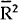 |
α | β | 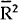 |
Nobs |
| 3 | 3.23 (0.71) |
0.49 (0.31) |
0.01 |
3.73 (0.68) |
0.17 (0.25) |
−0.02 |
4.76 (1.97) |
1.83 (0.72) |
0.03 |
40 |
| 6 | 2.87 (0.57) |
0.34 (0.27) |
0.02 |
3.66 (0.56) |
0.18 (0.16) |
−0.01 |
4.36 (1.46) |
2.11 (0.61) |
0.13 |
40 |
| 9 | 2.72 (0.46) |
0.34 (0.24) |
0.05 |
3.52 (0.46) |
0.08 (0.18) |
−0.02 |
3.38 (1.60) |
1.59 (0.15) |
0.09 |
40 |
| 12 | 2.58 (0.44) |
0.26 (0.24) |
0.03 |
3.34 (0.41) |
−0.02 (0.16) |
−0.03 |
2.73 (1.56) |
1.23 (0.48) |
0.05 |
40 |
| 15 | 2.60 (0.35) |
0.30 (0.16) |
0.08 |
3.30 (0.35) |
0.00 (0.14) |
−0.03 |
2.46 (1.48) |
1.05 (0.48) |
0.05 |
40 |
| 18 | 2.51 (0.32) |
0.21 (0.09) |
0.04 |
3.29 (0.33) |
0.04 (0.11) |
−0.02 |
2.02 (1.47) |
0.76 (0.37) |
0.03 |
40 |
| 21 | 2.43 (0.28) |
0.07 (0.90) |
−0.01 |
3.20 (0.29) |
−0.01 (0.10) |
−0.03 |
1.70 (1.44) |
0.42 (0.39) |
−0.01 |
40 |
| 24 | 2.45 (0.26) |
0.03 (0.10) |
−0.02 |
3.17 (0.28) |
−0.03 (0.09) |
−0.02 |
1.64 (1.37) |
0.25 (0.36) |
−0.02 |
40 |
| 36 | 2.59 (0.15) |
0.03 (0.03) |
−0.02 |
3.20 (0.21) |
0.03 (0.06) |
−0.02 |
2.33 (0.79) |
0.31 (0.13) |
0.03 |
40 |
NOTES. |
||||||||||
| GDP | CONSUMPTION | INVESTMENT | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| j | α | β | 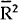 |
α | β | 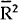 |
α | β | 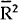 |
Nobs |
| 3 | 3.47 (1.09) |
0.26 (0.38) |
−0.02 |
3.27 (0.44) |
0.20 (0.23) |
−0.02 |
4.77 (3.74) |
1.51 (1.14) |
0.01 |
35 |
| 6 | 3.68 (0.88) |
0.31 (0.28) |
0.01 |
3.16 (0.41) |
0.09 (0.15) |
−0.02 |
5.44 (3.38) |
2.09 (0.81) |
0.09 |
34 |
| 9 | 3.94 (0.67) |
0.44 (0.21) |
0.08 |
3.14 (0.39) |
0.12 (0.15) |
−0.01 |
6.38 (2.71) |
2.40 (0.51) |
0.20 |
33 |
| 12 | 4.20 (0.42) |
0.54 (0.16) |
0.21 |
3.33 (0.26) |
0.21 (0.13) |
0.08 |
7.20 (2.13) |
2.63 (0.54) |
0.35 |
32 |
| 15 | 4.28 (0.29) |
0.55 (0.14) |
0.34 |
3.43 (0.18) |
0.28 (0.10) |
0.25 |
7.38 (1.98) |
2.63 (0.60) |
0.43 |
31 |
| 18 | 4.34 (0.23) |
0.56 (0.15) |
0.51 |
3.48 (0.16) |
0.29 (0.06) |
0.37 |
7.46 (1.86) |
2.49 (0.71) |
0.48 |
30 |
| 21 | 4.21 (0.22) |
0.49 (0.16) |
0.46 |
3.46 (0.16) |
0.30 (0.04) |
0.46 |
6.97 (1.60) |
2.06 (0.80) |
0.36 |
29 |
| 24 | 4.09 (0.23) |
0.41 (0.16) |
0.36 |
3.41 (0.15) |
0.26 (0.04) |
0.40 |
6.46 (1.30) |
1.52 (0.82) |
0.21 |
28 |
| 36 | 3.78 (0.34) |
0.05 (0.09) |
−0.03 |
3.18 (0.08) |
0.08 (0.04) |
0.05 |
5.42 (0.71) |
−0.42 (0.30) |
0.02 |
24 |
NOTES. |
||||||||||
The estimates for the latter period support the hypothesis that a positive slope of the yield curve implies faster growth in economic activity over the next one to two years. While the yield curve predicts changes in both consumption and investment, its predictive ability is higher for investment. The estimates suggest that a flat yield curve predicts growth in GDP over the next year of 4.2 percent. For every one percentage point steepening of the yield curve, the expected growth rate over the next twelve months increases by about 0.5 of a percentage point. The effect on investment is much more pronounced with a one percentage point steepening of the yield curve increasing investment growth over the next year by 2.6 percentage points.
Consistent with the theory presented above, the predictive power of the yield curve disappears in the long run. The yield spread has no predictive power for GDP, consumption or investment growth at a forecasting horizon of 12 quarters. It also has little predictive power in forecasting economic activity in the initial 6 months. The yield curve does best in forecasting economic activity in the 12 to 18 months horizons.
An examination of Table 1 shows that over the period from September 1972 to June 1982 the yield
curve had little predictive ability concerning the future path of economic activity. What little
information content there was, once again was more useful for predicting investment than
consumption. In fact the yield curve provided absolutely no information concerning the future
path of consumption; the highest 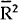 for any of the consumption
forecasting equations is −0.01. The comparable figure for the latter period is 0.46.
for any of the consumption
forecasting equations is −0.01. The comparable figure for the latter period is 0.46.
As mentioned above, the improved ability of the yield curve to predict economic activity can be attributed to changes in the operation and regulation of financial markets. Under the tap arrangements, the fixed rates were, in part, a reflection of market pressures. However, the relative constancy of the yield spread over the 1970's suggests that this reflection was less than complete. The increased ability of the yield curve to reflect monetary policy actions and expectations has played an important role in increasing the information content of the yield curve.
More general financial liberalisation has also played a role. The reforms which took place in the financial system in the early 1980's have made access to finance for both firms and households considerably easier. This has increased the potential for intertemporal substitution in both consumption and investment. One outcome of this liberalisation is that activity may now be more sensitive to interest rate changes. When interest rates are high, consumers delay consumption and conversely, when rates are low, consumers increase consumption. If the slope of the yield curve predominantly reflects current monetary policy, an upward sloping yield curve reflects relatively loose current or expected policy. Relatively low interest rates in turn induce consumers to substitute consumption and investment across time periods.
While the above results suggest that the slope of the yield curve is useful in predicting changes in real economic activity, it is also of interest to know whether or not it provides additional information over and above that provided by other indicators. The index of leading indicators should be a good summary statistic of information available to forecasters about the future course of the economy. Accordingly, the percentage change in the index over the previous quarter is included in the estimated forecasting equation. Given the previous results, only data for the period in which interest rates have been directly market determined have been used. The results are reported in Table 3.
| GDP | CONSUMPTION | INVESTMENT | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| j | α | β1 | β2 | 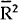 |
α | β1 | β2 | 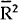 |
α | β1 | β2 | 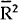 |
| 3 | 2.64 (1.08) |
0.23 (0.07) |
0.11 (0.43) |
0.10 |
3.18 (0.45) |
0.02 (0.06) |
0.19 (0.24) |
−0.04 |
2.39 (3.80) |
0.65 (0.21) |
1.09 (1.12) |
0.08 |
| 6 | 3.04 (1.03) |
0.17 (0.07) |
0.20 (0.35) |
0.14 |
3.09 (0.39) |
0.02 (0.04) |
0.08 (0.16) |
−0.05 |
3.53 (3.53) |
0.50 (0.27) |
1.75 (0.89) |
0.16 |
| 9 | 3.31 (0.80) |
0.15 (0.07) |
0.33 (0.26) |
0.22 |
2.94 (0.42) |
0.05 (0.03) |
0.09 (0.16) |
0.00 |
4.92 (2.86) |
0.35 (0.28) |
2.14 (0.61) |
0.24 |
| 12 | 3.73 (0.55) |
0.10 (0.06) |
0.45 (0.17) |
0.30 |
3.08 (0.29) |
0.06 (0.02) |
0.17 (0.13) |
0.15 |
6.22 (2.23) |
0.22 (0.21) |
2.45 (0.51) |
0.36 |
| 15 | 4.00 (0.34) |
0.06 (0.05) |
0.51 (0.12) |
0.37 |
3.25 (0.20) |
0.04 (0.01) |
0.25 (0.10) |
0.28 |
6.25 (1.90) |
0.24 (0.18) |
2.44 (0.52) |
0.46 |
| 18 | 4.23 (0.22) |
0.02 (0.04) |
0.54 (0.13) |
0.51 |
3.45 (0.14) |
0.01 (0.01) |
0.29 (0.06) |
0.35 |
6.59 (1.65) |
0.18 (0.15) |
2.36 (0.62) |
0.49 |
| 21 | 4.19 (0.23) |
0.00 (0.03) |
0.49 (0.15) |
0.44 |
3.47 (0.14) |
0.00 (0.01) |
0.30 (0.05) |
0.44 |
6.52 (1.51) |
0.09 (0.13) |
2.02 (0.77) |
0.34 |
| 24 | 4.04 (0.24) |
0.01 (0.03) |
0.40 (0.16) |
0.34 |
3.45 (0.10) |
−0.01 (0.01) | 0.26 (0.04) |
0.38 |
6.28 (1.28) |
0.03 (0.12) |
1.51 (0.81) |
0.18 |
| 36 | 3.81 (0.31) |
−0.01 (0.01) | 0.05 (0.09) |
−0.08 |
3.17 (0.08) |
0.00 (0.01) |
0.08 (0.04) |
0.00 |
5.92 (0.60) |
−0.10 (0.03) | −0.39 (0.24) | 0.03 |
NOTES. |
||||||||||||
As expected, the index of leading indicators is most useful in predicting economic activity in the very short run. In the GDP forecasting equation the index has a statistically significant coefficient for only the first three quarters, while in the investment equation it is only significant in the first quarter. In contrast to the index of leading indicators, the yield spread has little information content in the first few quarters but by four quarters shows considerable forecasting ability. The time profile of the forecasting ability of the yield curve is similar to that reported in Table 1.
We now turn to an examination of the monthly data. Table 4 presents the estimation results for forecasting equations of various horizons for the index of industrial production, dwelling approvals, and car registration. As in the above regressions, the dependent variable is the annualised percentage change in the relevant variable. Once again the slope of the yield curve is useful in forecasting the real variables although the results differ across the three variables. As was the case for GDP, the yield spread's ability to predict future changes in the production index increases through time out to about 18 months and then gradually declines. The yield curve is, however, less useful in predicting the changes in the production index than it is in predicting GDP changes. The results for car registrations exhibit a similar time profile to that of GDP and production although the usefulness of the yield curve in predicting changes in registrations is considerably less than is the case for the other variables. In contrast to the other measures of activity changes in housing approvals over the one month horizon are predicted by the yield curve. The yield curve remains useful in predicting future cumulative changes in housing approvals for about 18 months and is most useful at the 6 month horizon.
| PRODUCTION INDEX | DWELLING APPROVALS | CAR REGISTRATIONS | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| j | α | β | 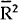 |
α | β | 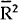 |
α | β |  |
Nobs |
| 1 | 7.35 (2.08) |
−1.22 (1.39) |
−0.01 |
36.17 (7.48) |
11.66 (2.67) |
0.06 |
54.26 (18.95) |
3.15 (3.94) |
−0.01 |
105 |
| 3 | 3.51 (1.12) |
0.59 (0.50) |
0.00 |
15.88 (5.21) |
8.50 (1.74) |
0.25 |
6.63 (4.40) |
1.88 (1.79) |
0.00 |
103 |
| 6 | 3.71 (0.82) |
0.79 (0.35) |
0.06 |
12.31 (5.84) |
7.34 (1.68) |
0.33 |
3.82 (3.95) |
2.73 (1.78) |
0.06 |
100 |
| 9 | 3.77 (0.65) |
0.90 (0.26) |
0.15 |
10.54 (6.51) |
6.37 (1.78) |
0.29 |
3.71 (3.64) |
2.84 (1.59) |
0.11 |
97 |
| 12 | 3.89 (0.57) |
0.93 (0.19) |
0.27 |
8.67 (6.73) |
5.12 (1.63) |
0.22 |
4.35 (3.52) |
3.11 (1.28) |
0.16 |
94 |
| 18 | 3.67 (0.58) |
0.74 (0.11) | 0.34 |
4.10 (6.07) |
2.22 (1.54) |
0.05 |
3.98 (4.28) |
2.77 (0.61) |
0.20 |
88 |
| 24 | 3.31 (0.54) |
0.52 (0.12) |
0.19 |
0.83 (4.31) | −0.02 (1.98) |
−0.01 |
2.13 (4.37) |
1.63 (0.50) |
0.07 |
82 |
|
NOTES. 1. The forecast horizon (j) is in terms of months. 2. Standard errors that are robust to serial correlation and conditional heteroskedasticity are reported in parentheses () below the coefficient estimates. 3. SPREAD is the spread between the yield on the 10 year Treasury bond and the 180 day bank bill. |
||||||||||
Footnotes
It is assumed that the growth rates and the yield spreads are stationary. While unit root tests are of limited value when the sample period is as short as that used in this paper, these tests do support the stationarity assumption. [3]
The tender system for Treasury notes was introduced in December 1979. [4]