RDP 9211: Dividends and Taxation: A Preliminary Investigation Appendix 1: Estimation with Panel-Data Models

Here we review the estimation of panel-data models. In particular we examine problems of estimation of panel-data models that contain lagged dependent variables.^[8]

Consider the linear model

where α_i is an individual specific component and ε_i,t is a mean-zero time-varying error. OLS will yield consistent coefficient estimates only if χ_i,t is uncorrelated with the error term (where the error term u_i,t = α_i + ε_i,t ). Two estimators have been developed to handle the systematic tendency of α_i to be higher for some units than for others: the random effects estimator and the fixed effects estimator.^[9]

If the individual specific component is assumed to be random with respect to the explanatory variables, the GLS (random effects) estimator provides efficient and consistent estimates. The GLS estimates can be obtained by OLS using the following transformation of equation (1)

where variables without the time subscripts arthe individual means,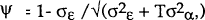 ; and where 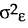is the variance of the time-varying error and 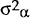is the variance of the individual specific error.

If however, α_i is not independent of X the random effects estimator will not give consistent estimates. In this case the individual effects are represented by a dummy variable for each individual (fixed effects estimator). Rather than include a dummy variable for each individual however, it is computationally easier to estimate the following model

The effect of subtracting individual means is to eliminate the fixed effect. The same result would be obtained if separate intercepts were estimated for each individual.

For consistency, both the fixed and the random effects estimators require that χ_i,t and ε_i,t are uncorrelated at all leads and lags. This condition is not met in the case of a model incorporating a lagged dependent variable, as E[Y_i,t−1 ε_i,t−1]≠0.

In this case the fixed and random effects estimators described above will not give consistent results and an alternate transformation must be used. Several authors have noted that the equation can be first differenced to remove the individual effects^[10]

Consistent estimates of the parameters in equation (4) can be obtained using instrumental variables. OLS cannot be used as (Y_i,t−1 − Y_i,t−2) is correlated with (ε_i,t − ε_i,t−1). Both Y_i,t−2 and Y_i,t−2 − Y_i,t−3 are often suggested as appropriate instruments.

Footnotes

This review draws heavily on the recent paper by Keane and Runkle (1992). [8]

See Amemiya and MaCurdy (1986) and Breusch, Mizon and Schmidt (1989). [9]

See Arellano and Bover (1990), Holtz-Eakin, Newey and Rosen (1988) and Keane and Runkle (1992). [10]