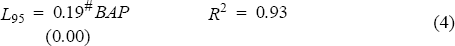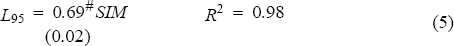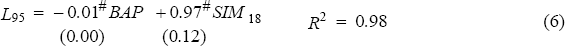RDP 9408: The Supervisory Treatment of Banks' Market Risk 5. Foreign Exchange Risk
November 1994
- Download the Paper 76KB
Consistent with the proposal on traded-debt instruments, the foreign exchange proposal attempts to measure the risks associated with banks' foreign exchange positions and apply a capital charge to cover potential losses. The foreign exchange proposal differs from the debt instruments proposal, however, in three respects:
- it is a generally simpler proposal;
- it does not attempt to draw distinctions between trading and non-trading positions. All foreign exchange positions are captured under the proposals; and
- it provides a comprehensive alternative to the standard method, which is intended to meet the needs of more sophisticated players in the foreign exchange market.
5.1 The Standard Method
The ‘standard’ method measures banks' foreign positions as the larger of its short and long positions measured in terms of the domestic currency. This approach is presently used in the UK to apply a capital charge to banks' foreign exchange positions and is used by the Reserve Bank in Australia to measure banks' foreign exchange positions.[14] This measure of foreign exchange exposure can be shown to be equivalent to the average of a banks' net and gross position in foreign currencies.[15] The implicit assumption behind this approach is that there is some, but not perfect, correlation between currencies.
The calculation of the capital charge can be illustrated by the following example. Consider the portfolio:
| Position $m |
||
|---|---|---|
| Currency | Long | Short |
| USD | 100 | |
| YEN | 100 | |
| CHF | 75 | |
| STG | 25 | |
| NZD | 80 | |
| Total | 180 | 200 |
The net position of the portfolio in this example is $20 million. The gross position is $380 million. The larger of the sum of the long positions or the sum of the short positions is $200 million. (Note that $200 million is also the average of the net and gross positions of $20 million and $380 million.)
Having measured the foreign exchange position, the proposal recommends the application of an 8 per cent capital charge. The capital charge generated by the portfolio above would be $16 million; 8 per cent of $200 million.
An adjunct to the capital requirements under the standard method is a ‘de minimis’ exemption. This exempts banks with foreign exchange positions which are small relative to their overall capital base from holding any capital against foreign exchange risk. The stated purpose of this exemption is to avoid onerous administrative burdens on banks with small foreign exchange operations. The maximum exemption which would be permitted is 2 per cent of the bank's capital base. In our example above, the bank would not be required to hold capital against the foreign exchange exposure if its capital base exceeded $10,000 million. If the bank's capital base is less than this amount (or its measured position larger), the bank will be required to hold capital against the entire exposure.
5.2 The Alternative, Simulation Method
The more sophisticated approach is one that would allow banks' to use a more complex simulation model to measure foreign exchange positions and risk, provided they are able to satisfy their national supervisors that they have the necessary measurement and control systems to implement such an approach.
The advantage of the simulation method is that it uses actual variance and co-variance relationships of exchange rates to more accurately track risk.
The simulation method is conceptually simple. Past exchange rates movements are used to revalue the bank's present foreign exchange positions and calculate simulated profits and/or losses which would have arisen if those positions had been held for two-week periods over the past 5 years. The capital requirement is then set in relation to the simulated losses which would have arisen during that period.
The simulation method involves;
- calculating the net aggregate value of the bank's current foreign exchange portfolio for every working day of the last five years, using actual exchange rates. The result is a series of 1,300 daily observations (5 days by 52 weeks by 5 years);
- calculating the change in the value of the portfolio over rolling two-week periods. This provides a time series of two-week changes in the value of the portfolio; and
- the capital charge would be levied, equal to the 65th largest loss (5th percentile from 1,300 observations), that is it represents a 95 per cent confidence interval of losses from the portfolio.
Where the simulation method is adopted, a ‘scaling factor’ has been introduced; an additional capital charge, equal to 3 per cent of the foreign exchange position measured by the standard method. The purposes of the scaling factor are stated to be:
- to determine the ‘toughness’ of the capital requirement;
- to produce a capital charge equivalent to that delivered by the standard method; and
- to ensure that at least a minimum capital charge was applied to banks' foreign exchange exposures.
The addition of the scaling factor detracts from the accuracy of the simulation method as a means of tracking risk. Moreover, the objectives of the scaling factor could be achieved by other means without the loss of this accuracy. For example, a change in the parameters of the simulation method, increasing the holding period of the portfolio to 3 weeks or the level of confidence required to 99 per cent, would achieve the first two of the objectives noted above, while a floor imposed on the amount of capital required to be held, perhaps based on the standard method, would achieve the goal of ensuring a minimum capital requirement.
5.3 Empirical Analysis of the Foreign Exchange Risk Proposal
The previous two sections described the proposed methodologies to calculated capital charges against foreign exchange risk. In this section, these methodologies are considered in the context of typical Australian bank exposures to foreign exchange and the exchange rate environment observed over recent years.
The data used in the statistical analysis are the weekly data on foreign exchange positions supplied by individual banks to the Reserve Bank. An ‘overall’ foreign exchange position, in terms of long and short positions in each currency, was calculated by summing the net open cash positions and foreign currency options positions[16] and consolidating across global operations. The foreign currency position information is categorised by currency, with nine major foreign currencies: US dollar, Canadian dollar, Japanese yen, Deutschemark, British pound sterling, New Zealand dollar, French franc and Swiss franc. Any residual foreign currency exposures, categorised as ‘other currencies’, were ignored in this analysis on the basis that they represented an insignificant proportion of the overall exposure.
Reported foreign exchange positions were assumed to be held for two weeks. The changes in the value of the portfolio over this fortnight were calculated on the basis of observed changes in exchange rates over the same period. The two-week convention, initiated by the Basle Committee in testing the proposal, is based on considerations of how rapidly bank portfolio losses due to exchange rate changes could be recognised and acted upon by banks. This is a conservative approach as it does not recognise that banks may change their positions rapidly in response to adverse changes in market conditions; hence a certain ‘comfort level’, whereby banks are assumed to have suffered greater losses than is probably the case, has been built into the study.
Losses and gains on all foreign exchange portfolio held between 1992 and 1994 were calculated for each reporting bank. It was possible therefore to calculate or isolate a loss consistent with coverage of two standard deviations of portfolio value movements (95 percentile losses). The 95 percentile losses are then used to assess the efficiency and coverage of each measure of foreign exchange risk. The relationship of the losses to the various measures of foreign exchange positions is calculated, and estimates of the optimal capital charge to be applied to each method found.[17]
The following capital charges associated with each of the banks' 95 percentile losses (L95) were calculated:
- standard Basle calculation without any de minimis exemption (BAP);
- capital charge based on simulation method using 95 percentile losses from the simulation process, without the 3 per cent scaling factor (SIM); and
- capital charge based on the simulation method using the 95 percentile losses from the simulation process (SIM), with the 3 per cent scaling factor (based on the standard Basle calculation, BAP).
Efficiency requires that there be a strong linear relationship between the positions measured and the losses incurred. The closer the relationship is, the more efficient is the capital charge. The equations below summarise the results of linear regression analysis.
Regression results for foreign exchange capital charges: [18]
# indicates that the variable is significant at the 1 per cent level. Standard errors are shown in brackets.
The results indicate that the simulation method is a more efficient measure of risk than the standard method. The R2 statistic on the standard method is 0.93, lower than that obtained for the simulation method with or without the 3 per cent scaling factor. The R2 statistic in equation 6 indicates that the scaling factor (BAP) has no impact on the ability of the simulation method to measure risk.
The coefficient on the variable SIM in equation 5 indicates that the simulation approach is also quite conservative – only about 70 per cent of the simulation capital charge is required to cover the 95 per cent losses incurred by the portfolios. These results are sensitive to the exchange rate environment against which they are tested. In a less volatile environment, such as that seen in recent years in Australia, the capital charges may appear even more conservative.
The coefficient on the variable BAP in equation 4 gives an indication of the size of the capital charge which should be applied under the standard method. Based on our data, the optimal charge to cover 95 per cent of all losses, is around 1.9 per cent. Doubling the losses from the data set and calculating the optimal weight for the standard method gave a result of 3.7 per cent, still well below the 8 per cent proposed by Basle. Put in other words, capital equal to around 4 per cent of the standard method would be adequate to cover twice the hypothetical losses in the data set.
This is considerably lower than the 8 per cent recommended charge. The Basle Committee have acknowledged the conservative nature of their 8 per cent capital charge. Their justification for the maintenance of 8 per cent includes the difficulty in monitoring reported positions, particularly intra-day exposures, and the difficulty in measuring risk associated with options and other derivative products.
In summary, the results indicate that for Australian conditions, an 8 per cent charge on the standard method of calculating foreign exchange exposures is very conservative. The results also show that the alternative simulation method is a more efficient measure of risk than the standard method and that there is little need for a minimum scaling factor.
Footnotes
The Reserve Bank also applies overnight limits on banks' foreign currency exposures. [14]
The net position is defined as being the absolute difference between long and short positions; the gross position is the sum of all positions regardless of sign. [15]
The Reserve Bank of Australia has a two-tier system for monitoring banks' exposures from foreign currency options. Banks that have sound mathematical models to calculate a “cash equivalent” of their foreign currency exposures generated by options written or held may use these to calculate the extent of the exposure. Bank with less sophisticated systems calculate foreign exchange options positions at face value. Both tiers of banks were used in this analysis as a statistical homogeneity test established that the tiers were not significantly different. [16]
One of the most common problems encountered in cross sectional regression analysis of this type is heteroscedasticity, where the variance of the errors is not constant. In this case, it was found that variance increased with the size of the positions held. The heteroscedasticity was appropriately corrected for by performing weighted least squares estimation using the sum of Net and Gross positions as a scaling factor. [17]
Strong collinearity exists between the two explanatory variables in equation 6. The lack of significance of the BAP variable is a reflection of this phenomena. [18]