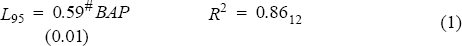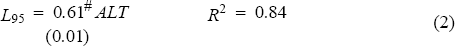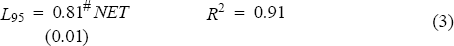RDP 9408: The Supervisory Treatment of Banks' Market Risk 4. Traded-debt securities
November 1994
- Download the Paper 76KB
The first of the proposals, and the most complex, covers market risk on traded-debt securities and related instruments. Although banks carry interest rate risk on many of their assets, the impact of changing interest rates is most obvious, and quantifiable, when looking at traded-debt instruments and debt-derivative products.
Under the proposed arrangements, the capital requirement for securities in the trading book consists of two separately calculated charges:
- the first relates to credit risk (and is termed ‘specific risk.’) It is defined as the risk that the price of a particular security will rise and fall with changes in the creditworthiness of the issuer. The capital charge arising from specific risk is intended to replace that levied under the present credit based capital requirements. However, as shown below, the basis of calculating the capital requirement for credit risk varies from that adopted under current capital adequacy arrangements; and
- the second capital charge will cover the ‘general market risk’, of the portfolio; that is, the risk of price movements arising from changes in the general level of interest rates.
4.1 Specific Risk
Specific risk applies to all long and short trading positions in debt instruments and in related derivatives. This differs from the current capital adequacy arrangements where only long positions in debt instruments (i.e. assets actually held) are subject to a capital charge. The broadening of the arrangements to include short positions recognises that the creditworthiness of an issuer can improve or deteriorate over time, and therefore the price of those particular securities can rise and fall relative to those of other issuers.[3]
Under the proposals, the following capital charges are applied to cover specific risk:
| Commonwealth Government securities | 0.00% |
| Qualifying securities: | |
| less than 6 months residual maturity; | 0.25% |
| between 6 and 24 months residual maturity; and | 1.00% |
| greater than 24 months residual maturity. | 1.60% |
| All other securities | 8.00% |
The ‘qualifying’ category includes debt and related instruments of local and state government authorities, other public sector entities, banks and high-quality corporates.
A corporate security will be deemed qualifying if it is:
- rated investment grade[4] by at least two credit rating agencies specified by the supervisor;
- rated investment grade by one credit agency and not less than investment grade by any other agency specified by the supervisor; or
- unrated, but deemed comparable to investment grade by the bank and the issuer has securities listed on a recognised stock exchange.
The specific risk charges outlined in this proposal differ in key respects from those applied under the capital adequacy guidelines; the most significant being the introduction of a concessional risk weighting for ‘qualifying’ debt. In the Australian market, this would mainly cover debt issues of high-quality corporates which, under the present standards, attract a uniform 8 per cent capital charge. The capital charges proposed for such issues would, therefore, be considerably lower than those levied under the present system. It would also open a large gap between capital charges applying to banks' holdings of debt securities of high-quality corporates and loans made to them by banks. This may provide incentives for banks to facilitate lending via the issue of debt, rather than lend directly to these companies or institutions. That approach, if adopted, would represent an important change in supervisory practice, carrying implications for the pattern of financing within the banking system.
4.2 General Market Risk
General market risk refers to the risk associated with changes in the level of interest rates.
The method proposed to calculate capital charges to cover general market risk requires that instruments[5] be slotted into a maturity ladder made up of thirteen maturity bands. A capital requirement is then determined based on the concept of potential change in the value of the portfolio.
For each position within a given time band, a calculation is performed to estimate potential change in value. The change in value of any particular position will reflect three factors:
- the size of the position itself.
-
the change/s in yield assumed for the purposes of the calculation.
The larger the interest rate variation built into the calculation, the larger the potential loss, and therefore the more conservative any resulting capital charge will be. For the purposes of determining the capital charge, the standard method assumes that the change in yield should be sufficient to cover two standard deviations of historical movements in yields over a one-month period; and
-
the price sensitivity of the position to changes in yield.
The sensitivity of the underlying securities which make up a position to changes in rates is technically more complicated to calculate. Here a relatively simple modified-duration methodology is adopted.[6] Rather than calculate the actual duration of each security using individual cash flows, the standard method estimates the modified duration for each separate time band, based on an assumption that all securities carry an 8 per cent coupon rate, an 8 per cent yield and a maturity equal to the mid point of their time band.[7]
The assumed change in yield and the modified duration can then be combined to produce a single ‘market-risk weight’ for each time band. Current market values of individual positions are multiplied by the market-risk weight appropriate to their time band. These are summed within each time band to give a net open position which represents the potential change in the value of all positions in the time band.
Potential changes in value for each time band must then be combined in some way to provide a measure of the overall change in value of the portfolio. The simplest way to achieve this would be to simply net, within and across time bands, all of the measured potential changes in value. That simple netting approach is only appropriate if actual yield curve movements follow the yield curve movement assumed in the risk-weighting process. Underlying the risk-weighting process is an assumed yield curve shift ranging from 100 basis points at the short end to 60 basis points at the long end.[8] This assumes that when the yield curve shifts as a result, say, of a shift in short-term interest rates, the movement of the curve is always the same. That assumption can rarely be justified. The shape of the yield curve will tend to change with changing short-term yields. Further, securities within the same time band may not exhibit the same price changes due to factors such as small maturity differences and the liquidity of different issues.
To take these complexities into account, so-called ‘disallowance factors’ are introduced to cover:
- imperfect correlation of price between different securities within a given time band (‘basis risk’); and
- imperfect correlation of price across different time bands (‘yield curve risk’).
The following two sections describe these disallowances in some detail, and illustrate how they would impact on the calculation of the total capital charge.
4.2.1 Vertical Disallowances to Cover Basis Risk
Within any particular time band, long and short risk weighted positions are offset, leaving a net open position. However, in recognition of the fact that each time band will include positions whose maturities are not identical, a 10 per cent vertical disallowance is applied to one side of the matched positions in each time band.
To illustrate, consider a bank which held the following positions in the 6 to 12 month maturity band[9] on January 1, 1994:
| Coupon % |
Maturity |
Market value $m |
Market risk weight % |
Risk-weighted position $m |
|
|---|---|---|---|---|---|
| a | b | a x b | |||
| Treasury bonds | 12.5 | 30/09/94 | 3,571 | 0.70 | 25 |
| Telecom bonds | 13.0 | 15/11/94 | −571[10] | 0.70 | −4 |
| Bank bills | 7.5 | 15/11/94 | −1,429 | 0.70 | −10 |
Diagrammatically, this ‘portfolio’ can be considered as below.
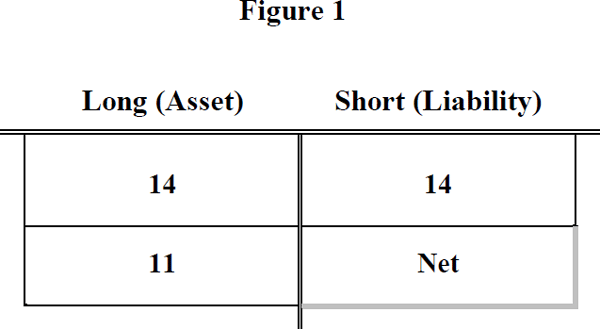
In this portfolio the sum of the weighted long positions in the time bands is $25 million and the sum of the weighted shorts is $14 million. The net open position in the time band is therefore a long position of $11 million. That amount is then carried forward to be used in the calculation of the horizontal disallowances covering yield curve risk (as described below.) The amount which has been offset attracts a capital penalty of 10 per cent. In this time band, $14 million of long and short positions have been offset against each other. The vertical disallowance of 10 per cent is applied, resulting in a capital charge of $1.4 million.
4.2.2 Horizontal Disallowances to Cover Yield Curve Risk
To cover yield curve risk, the standard method aggregates the thirteen time bands into three time zones and applies horizontal disallowances to cover opposite positions in different time bands and zones. The concept of capital charges based on offsetting positions in different time bands is analogous to that described above for vertical disallowances for offsetting positions within time bands. For example, where a bank has a net long risk-weighted position in the first time band (0–1 month maturity) and a net short position in the second time band (1–3 month maturity), the two positions may not be offset without taking into consideration the lack of price correlation between positions in the two time bands. As the differences in maturity are greater between time bands than within time bands, the disallowances factors applied are correspondingly higher.
The horizontal disallowance structure is summarised below.
| Time band |
Within the zone % |
Between adjacent zones % |
Between zones 1 and 3 % |
|
|---|---|---|---|---|
| Zone 1 | up to 1 month | |||
| 1 to 3 months | 40 | |||
| 3 to 6 months | ||||
| 6 to 12 months | ||||
| 40 | ||||
| Zone 2 | 1 to 2 years | |||
| 2 to 3 years | 30 | 150 | ||
| 3 to 4 years | ||||
| 40 | ||||
| Zone 3 | 4 to 5 yearsover | |||
| 5 to 7 years | ||||
| 7 to 10 years | 30 | |||
| 10 to 15 years | ||||
| 15 to 20 years | ||||
| over 20 years |
To illustrate, if the bank has net open positions in each time band as follows:
| Time band |
Market value $m |
Market-risk weight % |
Risk-weighted position $m |
Net position in zone $m |
|
|---|---|---|---|---|---|
| Zone 1 | up to 1 month | 100 | 0.00 | – | |
| 1 to 3 months | 500 | 0.20 | 1 | (3) | |
| 3 to 6 months | (3,750) | 0.40 | (15) | ||
| 6 to 12 months | 1,570 | 0.70 | 11 | ||
| Zone 2 | 1 to 2 years | 1,429 | 1.40 | 20 | |
| 2 to 3 years | (1,364) | 2.20 | (30) | (15) | |
| 3 to 4 years | (167) | 3.00 | (5) | ||
| Zone 3 | 4 to 5 years | 685 | 3.65 | 25 | |
| 5 to 7 years | 559 | 4.65 | 26 | ||
| 7 to 10 years | (172) | 5.80 | (10) | 40 | |
| 10 to 15 years | (133) | 7.50 | (10) | ||
| 15 to 20 years | 103 | 8.75 | 9 | ||
| over 20 years | 10.00 | – | |||
| Total | 22 | (a) |
The capital charges within time zones will be:
| Zone 1 | (0.4 × 12) | 4.8 | |
|---|---|---|---|
| Zone 2 | (0.3 × 20) | 6.0 | |
| Zone 3 | (0.3 × 20) | 6.0 | |
| 16.8 | (b) |
The capital charges between time zones:
| Zone 1/2 | nil | ||
|---|---|---|---|
| Zone 2/3 | (0.4 × 15) | 6.0 | |
| Zone 1/3 | (1.5 × 3) | 4.5 | |
| 10.5 | (c) |
The capital charge against general market risk in this case will be $49.3 million; the sum of the totals at (a), (b) and (c) above.
The capital charge calculated for the net open portfolio position, plus the vertical and horizontal disallowance factors calculated within and across time bands, can be added to yield a figure, measured in dollar terms, of the capital charge for general market risk. To that total is added the separately calculated capital charge for specific risk to give the full capital requirement for the trading book of debt instruments.
4.3 Underlying Assumptions
The previous sections describe the calculation of the capital charges under the standard method proposed by the Basle Committee. The calculation of capital charges on general market risk in the debt securities proposal relies on assumptions relating to:
- the volatility of interest rates;
- the structure of disallowance factors; and
- holding periods.
The following three sections consider the appropriateness of these assumptions in the context of the Australian market.
4.3.1 Volatility Assumptions
The proposal specifies interest rate (yield) shocks across the maturity profile of between 100 basis points for debt with maturities up to a year, to 60 basis points for instruments with maturities of 10 years or more. The appropriateness of capital charges generated by the model will depend therefore, on whether those changes in yield are representative of the volatility observed in the local market. If volatility is less than assumed, the resulting capital charge will be too high. Conversely, if volatility is greater than assumed, capital charges would be insufficient to cover the required proportion of losses.
To test the plausibility of the assumptions, they were measured against actual volatility of interest rates in the Australian market over recent years. Figure 2 shows the results of that analysis.
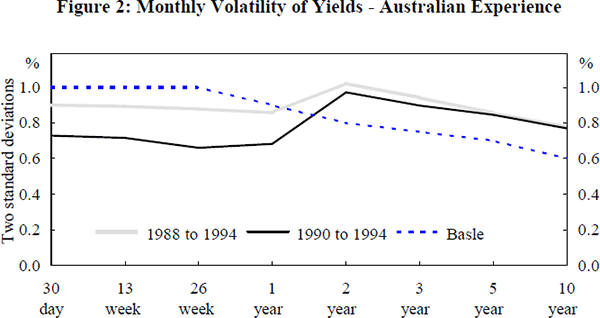
Levels of interest rate volatility vary depending upon the time period examined. Australian volatility has declined since 1990, especially at the short end of the yield curve. While the volatilities assumed in the proposal involve some overstatement at the short end of the yield curve, there was a tendency for some understatement of volatility at the medium to longer end. Those differences will lead to some misspecification of the capital charges. However, in a well-diversified portfolio, it may be that the effects of these departures from the Basle assumptions balance one another out.
4.3.2 Vertical and Horizontal Disallowances
A system of disallowances can be viewed as a means of improving the accuracy of the standard model. However, to be effective, the disallowance factors should bear a direct relationship to the price correlation between securities of different maturities; a factor which will also vary according to local market conditions. The appropriateness of both the horizontal and vertical disallowances can be assessed by looking directly at the correlations between the prices of different securities.
Table 2 sets out actual price variations of securities across different points of the yield curve based on an analysis of five years of actual data. It shows that the degree of correlation of monthly price changes is relatively high across securities of different maturities. For the Australian market, the proposed horizontal disallowances would appear to overstate significantly the true degree of price variation across the maturity spectrum.
| 30 day |
13 week |
26 week |
1 year |
2 year |
3 year |
5 year |
10 year |
15 year |
||
|---|---|---|---|---|---|---|---|---|---|---|
| 30 day | 1.00 | Zone 1 | ||||||||
| 13 week | 0.81 | 1.00 | ||||||||
| 26 week | 0.76 | 0.96 | 1.00 | |||||||
| 1 year | 0.66 | 0.86 | 0.92 | 1.00 | Zone 2 | |||||
| 2 year | 0.53 | 0.72 | 0.80 | 0.92 | 1.00 | |||||
| 3 year | 0.47 | 0.68 | 0.76 | 0.89 | 0.97 | 1.00 | ||||
| 5 year | 0.43 | 0.63 | 0.72 | 0.85 | 0.95 | 0.98 | 1.00 | Zone 3 | ||
| 10 year | 0.31 | 0.49 | 0.57 | 0.69 | 0.80 | 0.86 | 0.90 | 1.00 | ||
| 15 year | 0.28 | 0.51 | 0.51 | 0.61 | 0.80 | 0.85 | 0.90 | 1.00 | 1.00 |
4.3.3 Holding Periods
The modified duration methodology applies interest rate movements to the portfolio based on two standard deviations of monthly volatility of interest rates at various points along the yield curve. Potential losses are based on monthly movements in interest rates (yields). Implicit in this approach is the assumption that a banks will suffer losses incurred over a month before acting to close out positions or taking other action to minimise losses. Market practitioners have argued that this assumption is unrealistic and not representative of actual behaviour. Banks tend to liquidate unfavourable positions much more rapidly than assumed. If this were the case, the effect of this assumption would be an unduly harsh capital penalty.[11] The counter argument to this is that in many instances, traders do not close out unfavourable positions if they believe that the movement in market yields is merely an aberration.
4.4 Empirical Analysis of the Traded-Debt Securities Proposal
Two sets of tests were performed to assess the efficacy and coverage achieved by the capital charges generated under this proposal. The first involved testing the proposal against a small number of actual bank portfolios of debt instruments against actual interest rate movements. Comparisons were then made between losses that would theoretically have been recorded and the level of capital that would have been required under the proposal.
Because of the limited number of actual portfolios available, a second set of tests were conducted based on a series of randomly generated portfolios. These portfolios were created by assuming that the size of banks' long and short positions in time band followed a uniform distribution between $0 million and $100 million. Three hundred separate portfolios were generated by that method.
The portfolios were revalued at monthly intervals using actual yields from the Australian market over the period June 1988 to June 1993. Losses and gains are then calculated from the differences in the value of the portfolio, from month to month, over the five-year period. Two standard deviations of changes in the value of each portfolio form the benchmark against which the capital charges are compared.
Based on the sample of actual portfolios, the capital charge from the standard method proved to be very conservative when compared to the monthly gains and losses experienced by the portfolio. On average, the capital charge covered 99 per cent of all losses. If the portfolio is assumed to be held for a period less than the four weeks specified in the proposal, say for two weeks, then the coverage achieved by the capital charge increases dramatically. The capital charge is sufficient to cover all losses in the period examined (100 per cent coverage) and a considerable buffer of capital above the worst loss is maintained. Given that a shorter holding period for securities within a trading book is not an unreasonable assumption, the level of capital proposed by Basle, therefore, appears conservative.
The results from the simulation analysis on the hypothetical portfolios supports these results. On average, the capital charge covered 99 per cent of the simulated losses on these randomly generated portfolios. The 95 percentile losses (those corresponding to two standard deviations of movements in the value of the portfolio) were compared with the standard capital charge. In no case was the capital charge inadequate to cover two standard deviations of losses, and in most cases, excess capital above this level of loss remained. The conservatism is further emphasised by the fact that the portfolios generated did not take into account the interest rate environment and the fact that actual portfolios will reflect the shape of the yield curve.
An appropriate capital charge is required to do more, however, than to ‘cover’ all, or most losses. The ideal capital charge is one which tracks risk well. Put another way, there should be a strong relationship between the capital charge and the risk in the portfolio. (In this study, the proxy for risk is two standard deviations of movements in the value of the portfolio; or, in other words, the 95 percentile loss.) The analysis indicates that such a relationship exists between the capital charge proposed by Basle and the losses incurred by the portfolios. The Basle method was tested against several alternatives to assess its relative performance. An R2 statistic was used to quantify the ‘fit’ of the losses to the capital charge.
The equations below detail the results of regression analysis of the linear relationship between the 95 percentile losses (L95) and three capital charges, including that proposed by Basle. These capital charges are those derived from:
- the standard method proposed by Basle (BAP);
- a simplified version of the Basle model, using only 5 time bands and 2 time zones and a correspondingly simplified horizontal disallowances structure, (ALT); and
- an even simpler model (NET) which is the Basle model excluding the vertical and horizontal disallowances.
Regression results for debt securities capital charges:[12]
# indicates that the variable is significant at the 1 per cent level. Standard errors are shown in brackets.
Equation 1 indicates that there is a strong relationship between the Basle capital charge and 95 percentile losses. It is interesting, however, that the Basle capital charge is out-performed by the much simpler net model. This implies that the horizontal disallowances do not improve the ability of the Basle capital charge to measure risk.[13] The Basle Committee justifies the additional complexity of the horizontal disallowance structure on the added accuracy it provides to the measurement of risk. The results obtained here question that argument, and suggest that even simpler measures are equally effective.
The coefficients on the capital charge variables in equations are shown to be all less than unity. This implies that, on average, the capital charge overstates the risk associated with the portfolio; less capital would be required to cover the losses observed. In the case of the standard capital charge (BAP), approximately 60 per cent of the proposed capital charge would be sufficient to cover 95 per cent of all changes in the portfolio value.
The debt securities proposal is the most complex of the three market-risk proposals; the concept of vertical and horizontal disallowances is unique to the debt securities proposal, as is the use of more sophisticated risk measurement techniques such as modified duration. Empirical analysis indicates that the capital charge generated is quite conservative; measured against a 95 per cent confidence interval; it is more than sufficient to cover most losses which would be faced by a bank over a one month period. However, data from the simulation analysis indicates that simpler versions of the Basle method perform equally well or better in covering losses.
Footnotes
For the purposes of the calculation, offsetting positions in identical security issues are excluded. [3]
For example, rated Baa or higher by Moodys and BBB or higher by Standard and Poors. [4]
Instruments which are included are: long and short positions in physical debt securities; notional underlying positions of derivative instruments such as futures, forwards and swaps (both legs of the swaps are included, each in their appropriate time band); and options on the basis of the probability of their being exercised (delta equivalent basis). [5]
Duration is a technique used to measure the price sensitivity (i.e. risk) of a security or a portfolio. Price sensitivity is greater for securities (or portfolios) with longer maturities and/or lower coupon rates. Duration provides a useful measure of this price sensitivity by taking both factors into account. In mathematical terms, the concept of ‘modified duration’ measures the price sensitivity of a bond to a small change in interest rates. [6]
The proposals allow banks with sophisticated risk management systems to calculate the exact duration for all individual positions, and use these more accurate measurements in calculating risk-weighted positions. [7]
These assumed volatilities are based on empirical work performed by the Basle Committee using data from different international interest rate environments. [8]
The risk-weighted position of securities within the 6 to 12 month time band is calculated as 0.7 per cent of market value. This represents the product of the duration weight of 0.7 and the assumed change in yield of 100 basis points. [9]
Negative numbers represent liabilities, or short positions. [10]
It should be noted also that the monthly holding period is inconsistent with the traded equity and foreign exchange proposals which only assume a two-week holding period. [11]
Note that where regression equations are estimated without the inclusion of a constant, it is possible to obtain negative R2 values. [12]
The same cannot be said regarding vertical disallowances as the simulation process only includes one type of security per time band – therefore basis risk between offsetting securities in the same time band is not observed. [13]