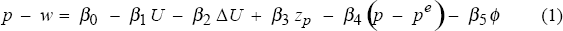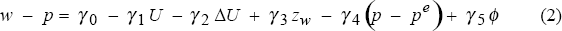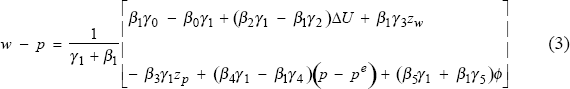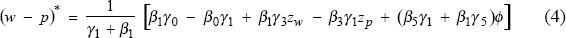RDP 9509: Australian Wage and Price Inflation: 1971–1994 2. Imperfect Competition Model of Inflation

The large and persistent fluctuations in labour's income share can be explained by adjustment costs and real wage rigidities within a neoclassical model with price-taking firms. In this model the real wage remained high relative to productivity following the 1974 wage shocks, raising labour's income share and increasing unemployment.^[1] Eventually the real wage was driven down relative to productivity by the higher unemployment and labour's income share returned to its pre-shock level. The fact that unemployment did not simultaneously return to its pre-shock level implies the story is more complicated. One explanation is that the observed unemployment was voluntary or frictional and there was no involuntary unemployment. Casual observation suggests this is incorrect. A second explanation is that labour supply increased during the adjustment and that the existing real wage and labour's income share were still too high compared with their full employment values. While this may be true there seems little obvious market driven pressure to further lower real wages at present.^[2]

Modelling the Australian economy using a price taking model is inconsistent with the observation that firms appear to set prices and that labour market outcomes are the result of collective bargaining between labour and firms (or possibly labour, the government and firms). It may be more appropriate, therefore, to model Australian wage and price inflation within an imperfect competition model.

In the ‘standard’ imperfect competition model firms maximise profits by holding a desired markup of price on wages.^[3] This implies they hold a desired real wage. Simultaneously, labour's desired real wage is a decreasing function of the level of unemployment since the bargaining position of labour deteriorates as unemployment rises. In the long run, the desires of labour must be consistent with those of firms and this is achieved by changes in the level of unemployment. When the desires of labour and firms are consistent, inflation is stable and the corresponding level of unemployment is termed the non-accelerating inflation rate of unemployment (NAIRU). Away from the NAIRU the desires of firms and labour are not consistent and one or both parties are disappointed with the outcome. In this version of the model, the disappointment is due to the mistaken price expectations of firms and labour which result from unexpected changes in the rate of inflation.

An explanation of the shifts in Australian income shares within an imperfect competition model is set out in Figure 3. It is assumed that labour productivity is constant and equal to 1. It is also assumed that the labour force is fixed so that unemployment U can be shown on the horizontal axis along with employment L.^[4]

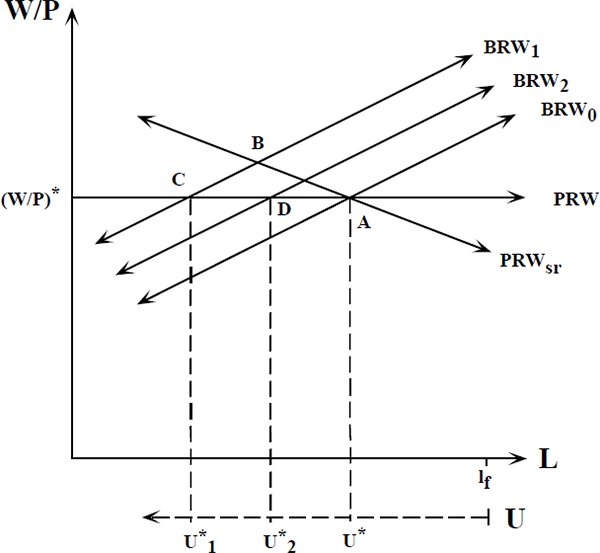
The horizontal product real wage (PRW) curve is the firm's desired real wage. While there is no consensus as to how imperfectly competitive firms adjust prices, there is general agreement that in the long run the markup of price on wages is constant and, therefore, the PRW is constant.^[5] The curves marked BRW are the desired real wage which labour bargains for. The BRW curves slope upward to reflect the improved bargaining position of labour as unemployment falls.

At A the real wage desires of labour and firms are matched by an unemployment rate of U^* and inflation is stable. Wage shocks such as those in the early 1970s would lead to the BRW₀ curve shifting to BRW₁ where each level of unemployment is associated with a higher desired real wage. Due to adjustment costs, the firm's desired short-run PRW curve is downward sloping and the economy initially shifts to B where there is a higher real wage and labour's share of income as well as higher unemployment.^[6] In the long run the economy will eventually shift to C with even higher unemployment but with the real wage returning to its long-run level (W/P)^*. If before adjustment is complete the economy experiences a wage shock, such as associated with the wage pause and the Accord, the desired real wage curve of labour will shift down to BRW₂ and the economy moves towards D.

In this model the real wage and labour's income share eventually return to their long-run level. The higher level of unemployment reflects the fact that labour's real wage demands are still greater at each level of unemployment than before the initial shock. In the new long run, the real wage demands of labour just balance those of profit maximising firms. For the economy to return to A the demands of labour would have to be reduced further shifting the BRW curve back to BRW₀ which implies a period of adjustment where the real wage is below its long-run level.

In this simple imperfect competition model, short-run deviations in real wages from their long-run level are due to mistaken price expectations and adjustment costs. However, if these are the only causes of the fluctuations in the real wage then the adjustment appears slow. The increase in real wages relative to productivity following the 1974 wage shocks lasted around 12 years and it took nearly two business cycles before firms and labour corrected their mistaken price expectations and the wages share returned to its pre-shock level.

Despite this issue the imperfect competition model of inflation is used to derive a simple markup model of prices for a closed economy.^[7] We can write the firm's desired markup as:

and labour's desired real wage as:

where p, p^e, w, U and ϕ are prices, expected prices, wages, the unemployment rate and productivity respectively and the lower case variables are in logs. All coefficients in equations (1) and (2) are positive. The variables z_w and z_p capture shifts in the bargaining position of labour and firms respectively.^[8] For labour, z_w includes unemployment benefits, tax rates, and measures of labour market skill mismatch. Similarly for firms, z_p includes measures of the firm's competitive environment or monopoly power, indirect taxes, and non-labour input costs including oil prices. The unemployment term in the firm's desired markup equation is simply an output measure using Okun's law. If the desired markup is independent of the level of demand then β₁ = 0.

These two equations represent the desired claims of firms and labour on the real output of the economy. By design the ex post real wage of labour must always be equivalent to the inverse of the firms markup. We can, therefore, eliminate the real wage from (1) and (2) to provide an expression for the unemployment rate. Alternatively, we can eliminate the unemployment rate to provide an expression for the real wage:

Defining the long run by setting ΔU = 0 and p = p^e then the long-run real wage is:

Therefore, the long-run real wage and markup are functions of productivity. Furthermore, if firms price independently of demand as in Figure 3 then the real wage in the long run is independent of wage pressures shocks z_w. In contrast, changes in the competitive environment captured by z_p do affect the long-run real wage.

Two issues concerning this model should be raised. First, for labour and firms to maintain stable income shares in the long run and for these shares not to continually rise or fall with trend productivity, the coefficient on productivity in the long-run real wage equation 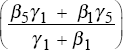must equal unity. This condition is met if β₅ = 1 and γ₅ = 1.^[9] However, if firms price independently of demand and maximise profits (which implies β₅ = 1) then this condition will hold irrespective of γ₅. In the general case when β₁ ≠ 0 the impact of productivity on labour's real wage desires is important. Feedback mechanisms through the impact of persistent unemployment on the aspirations of labour could lead the above coefficient on productivity to equal unity in the long run. However, there is no a priori reason why this condition should be met in the short run.^[10]

The second issue is whether the model as outlined in equations (1) and (2) is identified.^[11] If the equations represent the bargaining behaviour of labour and firms then it can be expected that the variables which impact on the bargaining behaviour of one group will automatically impact on the other. For example, union strength will not only affect labour's bargaining position but also how firms conduct negotiations with labour. In this case z_w and z_p enter both the price and wage equations and the model is not identified.

Footnotes

The result that high real wages increase labour's income share is not straight-forward. High real wages reduce labour input relative to capital and raise the marginal product of labour. Depending on the size of the increase in average productivity, labour's income share may rise or fall. Given that wage shocks appear to raise labour's income share for a considerable time it would appear that the increase in productivity does not match the rise in real wages, at least not in the short to medium term. [1]

For a comprehensive survey on the interrelationship between unemployment, Phillips curves and real wages, see Bean (1994). [2]

The ‘standard’ model is that of the Layard/Nickell tradition. For a detailed exposition, see Layard, Nickell and Jackman (1991) or Carlin and Soskice (1990). [3]

These simplifications allow the story to be told in two dimensions on a diagram. With steady state growth in productivity, the curves are simultaneously shifting upwards. Another result of the simplification of constant labour productivity is that increases in the real wage correspond to increases in labour's share of income. [4]

Normal cost markup and kinked demand curve models suggest the price level is largely insensitive to demand fluctuations. See Hall and Hitch (1939), Sweezy (1939), Layard et al. (1991), Carlin and Soskice (1990), Coutts et al. (1978), Tobin (1972), Bils (1987). [5]

In the short run firms may not fully pass on cost increases into prices for a number of reasons including menu costs and contracts. The reasons are loosely collected under the heading of ‘adjustment costs’. [6]

See Appendix A for a more detailed working of this model. [7]

For a detailed discussion of the theory underlying these shift variables see Layard, Nickell and Jackman (1991) or for a simple taxonomy of explanations see Coulton and Cromb (1994). [8]

This is the equivalent to assuming linear homogeneity between prices and unit labour costs. [9]

The basing of labour's wage claims on past rather than present productivity is sometimes referred to as real wage persistence. Many studies have highlighted the persistently high growth in labour's desired real wages as a major explanation of European unemployment following the slowdown in productivity growth after OPEC 1. See Bruno and Sachs (1985), Grubb, Jackman and Layard (1983). [10]

The model is not identified if adding a multiple of one equation to the other leaves the form of the equation unchanged. A number of authors, including Manning (1994), have raised doubts as to whether the imperfect competition model is identified. [11]