RDP 9601: Why Does the Australian Dollar Move so Closely with the Terms of Trade? 2. The Dynamic Properties of the Terms of Trade
May 1996
- Download the Paper 204KB
This section examines the dynamic properties of Australia's terms of trade. At issue is whether shocks have a permanent effect on the level of the terms of trade (in which case the terms of trade process contains a unit-root), or only a temporary effect (implying that the terms of trade are stationary, possibly around a trend).
In previous empirical research on the Australian real exchange rate, the terms of trade was characterised as a unit-root process (Blundell-Wignall and Gregory (1990), Blundell-Wignall, Fahrer and Heath (1993) and Gruen and Wilkinson (1994)). This characterisation was primarily based, however, on statistical tests which did not allow for a trend in the terms of trade. Visual inspection of Figure 1 above suggests a slight but noticeable downward trend in the terms of trade, suggesting that such a trend should be allowed for when examining the time-series properties of the terms of trade. When this is done, strong evidence emerges that the terms of trade exhibit only temporary deviations from a slowly declining trend.
We present evidence from three statistical tests: the Augmented Dickey-Fuller (ADF) test, the Dickey-Fuller (1981) Φ3 test and the Kwiatkowski, Phillips, Schmidt and Shin (1992) test. The ADF unit-root test is based on the regression:
where tott is natural log of the terms of trade in period t, Δ is the first difference operator, α is the constant or ‘drift’ term, and t is a linear time trend. The lag length on the lagged dependent variable, p, is chosen to eliminate serial correlation in the estimated residuals of equation (1). We set p = 4, and in our results in Table 1 below, show evidence of a lack of serial correlation in the residuals (based on the Ljung-Box Q statistic).[1]
| ADF statistic (with constant and trend) |
ADF statistic (with constant and no trend) | D&F ϕ3 test statistic |
Ljung-Box Q statistic |
|
|---|---|---|---|---|
| Sept 1969 – June 1994 | −5.04*** | −2.87* | 13.76*** | 19.44 |
| Sept 1969 – Dec 1986 | −4.08** | −1.61 | 9.99*** | 16.14 |
|
Notes: ***, **, and *, signify rejection of the relevant null hypotheses at 1%, 5%, and 10% levels of significance. The Ljung-Box Q Statistic is for the first 23 autocorrelations of the residuals for the full sample, and 16 for the truncated sample. |
||||
For the entire sample period, Sept 1969 – June 1994, Table 1 shows that the null hypothesis that the terms of trade possesses a unit root is rejected at the 1 per cent level of significance on the basis of both the ADF statistic with constant and trend and the Dickey-Fuller Φ3 statistic. Note, however, that the ADF statistic with constant term and no trend leads to rejection of the null hypothesis only at the 10 per cent level of significance. Thus, assuming no trend gives much weaker evidence against non-stationarity in Australia's terms of trade over the period.
Later in the paper, we generate forecasts of the real exchange rate beginning in 1987:Q1. Table 1 also reports the results of the statistical tests over a sample period ending before these forecasts begin. Estimation over this truncated sample period, Sept 1969 – Dec 1986, yields results that are qualitatively similar to those generated using the entire sample. The ADF statistic with constant and trend rejects the presence of a unit root at the 5 per cent significance level, while the Dickey and Fuller Φ3 statistic rejects the null hypothesis of non-stationarity at the 1 per cent level of significance.
In contrast to the ADF unit-root test, the Kwiatkowski, Phillips, Schmidt and Shin (KPSS) test has either trend or level-stationarity as a null hypothesis. It thus complements the ADF unit-root test. The KPSS test for trend-stationarity involves regressing the variable under examination against a constant and time trend and calculating the following modified LM statistic:
where 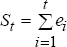 is
the partial sum process of the regression residuals, ei,
s2(k) is a consistent estimator of the long run error variance
based on a Bartlett window adjustment using the first k sample autocovariances as
advocated by Newey and West (1987), and T is the sample size.
is
the partial sum process of the regression residuals, ei,
s2(k) is a consistent estimator of the long run error variance
based on a Bartlett window adjustment using the first k sample autocovariances as
advocated by Newey and West (1987), and T is the sample size.
Table 2 presents KPSS test statistics, calculated over the two sample periods, Sept 1969 – Dec 1986, and Sept 1969 – June 1994, for different values of k. The null hypothesis of trend-stationarity in Australia's terms of trade is accepted at a 5 per cent level in all cases.
| Lag truncation parameter | KPSS test statistic | KPSS test statistic |
|---|---|---|
| k | Sept 1969 – Dec 1986 | Sept 1969 – June 1994 |
| 2 | 0.139 | 0.114 |
| 4 | 0.095 | 0.077 |
| 6 | 0.081 | 0.063 |
| 8 | 0.077 | 0.059 |
| 10 | 0.078 | 0.059 |
| 12 | 0.082 | 0.061 |
|
Note: The null hypothesis of stationarity around a constant and trend is rejected for values of the KPSS statistic greater than 0.216, 0.146, and 0.119 at the 1%, 5% and 10% significance levels. |
||
Thus, over either sample, the three statistical tests provide evidence that Australia's terms of trade exhibit only temporary fluctuations around a slowly declining trend.
2.2 Modelling Australia's Terms of Trade
For the forecasting exercise to follow, we need a time-series model of the Australian terms of trade. For simplicity, we restrict our specification search to autoregressive models, AR(1) to AR(8). Given the evidence from the last section, each model includes a constant and linear trend. Thus, we estimate the following models:
where tott is the log terms of trade in period t, α is a constant, t is a linear time trend, and ut is a mean-zero error term. Estimation is over the truncated sample period, 1971:Q3 – 1986:Q4, so that the preferred specification is determined using data preceding the forecast period (which begins in 1987:Q1).
Summary statistics for the estimated models are presented in Table 3. On the basis of both the Akaike and Schwarz information criteria, the AR(5) model is the preferred specification for Australia's log terms of trade. We therefore use this specification to generate out-of-sample forecasts of the terms of trade throughout the forecast period.[2]
| Model | Akaike information criterion (AIC) | Schwarz information criterion (SIC) |  |
Ljung-Box Q statistic |
|---|---|---|---|---|
| AR(1) | −161.90 | −155.52 | 0.90 | 20.01 |
| AR(2) | −160.45 | −151.94 | 0.90 | 18.15 |
| AR(3) | −162.02 | −151.38 | 0.90 | 21.98** |
| AR(4) | −163.85 | −151.09 | 0.90 | 19.41* |
| AR(5) | −175.21 | −160.32 | 0.92 | 15.94 |
| AR(6) | −174.51 | −157.49 | 0.92 | 13.47 |
| AR(7) | −172.53 | −153.39 | 0.92 | 12.93 |
| AR(8) | −172.78 | −151.51 | 0.92 | 11.81 |
|
Note: The models are estimated over the period Sept 1971 – Dec 1986. **, and *, signify rejection of the null hypothesis at the 5% and 10% levels of significance. The Ljung-Box Q Statistic is for the first 15 autocorrelations of the residuals. |
||||
Table 4 presents coefficient estimates for this preferred AR(5) model:
Note that the trend term is negative and highly significant, and that the sum of the
coefficients on the lagged dependent variables,  = 0.72, is less
than unity, consistent with the earlier evidence that the terms of trade exhibit temporary
fluctuations around a declining trend.
= 0.72, is less
than unity, consistent with the earlier evidence that the terms of trade exhibit temporary
fluctuations around a declining trend.
| Constant | Trend | tott–1 | tott–2 | tott–3 | tott–4 | tott–5 | |
|---|---|---|---|---|---|---|---|
| coeff. | 1.37 | −0.0012 | 0.77 | 0.16 | 0.07 | 0.15 | −0.43 |
| (s.e.) | (0.29) | (0.0003) | (0.12) | (0.16) | (0.16) | (0.16) | (0.12) |
|
Note: Estimation Period: Sept 1971 – Dec 1986. |
|||||||
Finally, Figure 2 shows the actual log terms of trade over the sample period, 1971:Q3–1986:Q4, and the estimates generated from the preferred AR(5) model. The in-sample fit of the preferred model is clearly quite good.

Footnotes
See Appendix A for further details on all the statistics reported here. [1]
While we keep the same AR(5) specification, we do re-estimate the model parameters as each new quarter of data becomes available in the forecast period. [2]



