RDP 9601: Why Does the Australian Dollar Move so Closely with the Terms of Trade? 4. Predictable Real Exchange Rate Changes and Excess Returns
May 1996
- Download the Paper 204KB
4.1 Forecasting the Real Exchange Rate
We now turn to the out-of-sample forecasting performance of the two exchange rate models. Almost without exception, out-of-sample forecasting evaluations by previous researchers use actual future values of the explanatory variables to generate exchange rate forecasts.[6] By contrast, as we have stressed, the forecasts we generate are truly ex ante: they use only information available at the time the forecasts are made.
We use recursive estimation to generate out-of-sample forecasts. This involves initially estimating the models over a sample period up to, but not including, the first quarter in which forecasts are made, 1987:Q1.[7] The estimated terms of trade model is used to generate out-of-sample forecasts for the terms of trade from one to eight quarters ahead. These forecasts are then used with the preferred exchange rate models to generate forecasts of the real exchange rate change from one to eight quarters ahead.
The sample is then extended by one quarter to include data from 1987:Q1, and the models' parameters re-estimated. This leads to new out-of-sample forecasts for the terms of trade and the change in the real exchange rate from one to eight quarters ahead. Repeating this procedure for each subsequent quarter, up to and including 1994:Q2, generates 30 out-of-sample forecasts of the expected change in the trade-weighted real exchange rate for each forecast horizon from one to eight quarters ahead.
We can now evaluate the models’ out-of-sample forecasting performance by regressing the actual, ex post real exchange rate change on its ex ante forecast:
where  is
the expectation at time-t based on real exchange rate model x = A,B. If the
model contains no useful information for k-period-ahead forecasts of the exchange rate
change, the coefficient estimate of β will be insignificantly different from zero.
In this case, the exchange rate model forecast does not out-perform those of a random walk. If,
however, β is significantly different from zero, then the model contains
significant information about future movements of the real exchange rate. Further, if this
coefficient is insignificantly different from unity, this suggests the model generates unbiased
forecasts of the real exchange rate change k-quarters ahead.[8] In the results
reported below, we test two null hypotheses, H01: β = 0 and
H02: β =1.
is
the expectation at time-t based on real exchange rate model x = A,B. If the
model contains no useful information for k-period-ahead forecasts of the exchange rate
change, the coefficient estimate of β will be insignificantly different from zero.
In this case, the exchange rate model forecast does not out-perform those of a random walk. If,
however, β is significantly different from zero, then the model contains
significant information about future movements of the real exchange rate. Further, if this
coefficient is insignificantly different from unity, this suggests the model generates unbiased
forecasts of the real exchange rate change k-quarters ahead.[8] In the results
reported below, we test two null hypotheses, H01: β = 0 and
H02: β =1.
Before estimating equation (9) and conducting these hypothesis tests, however, there are two technical difficulties to be addressed. The first is that the OLS estimate of β may be biased in small samples, if the error terms in the terms of trade equation (equation 4) and in the process driving the real exchange rate are correlated (Stambaugh 1986). This problem is potentially serious as the sample size is indeed small, especially for longer-horizon forecasts.[9]
The second difficulty is that, for k > 1, the forecast horizon extends beyond the sampling interval which induces (k-1)th-order serial correlation in the regression residuals, εt+k,t. This problem can be dealt with by using the Newey and West (1987) consistent estimate of the asympotic covariance matrix, and we report results based on this approach. Unfortunately, while it is valid asympotically, there is no guarantee that this approach gives accurate results in small samples.
To deal with both these small-sample problems, we therefore conduct Monte Carlo simulations, described in Appendix C, to derive estimates of the exact distributions of relevant statistics.
Tables 5a and 5b report the results for models A and B. They show OLS estimates of the
coefficients in equation (9), R2 s, and
adjusted values,  ADJ and
R2ADJ, derived by subtracting from the OLS estimates,
ADJ and
R2ADJ, derived by subtracting from the OLS estimates,
 and
R2, median estimates from Monte Carlo simulations assuming the real exchange
rate is unforecastable. For the hypothesis test H01: β = 0, the tables
show Newey-West t-statistics and their associated marginal significance levels against
the alternative β > 0, denoted MSLNW, as well as results
derived from the Monte Carlo simulations. For H02: β = 1, the Tables
show only marginal significance levels from the Monte Carlo simulations.
and
R2, median estimates from Monte Carlo simulations assuming the real exchange
rate is unforecastable. For the hypothesis test H01: β = 0, the tables
show Newey-West t-statistics and their associated marginal significance levels against
the alternative β > 0, denoted MSLNW, as well as results
derived from the Monte Carlo simulations. For H02: β = 1, the Tables
show only marginal significance levels from the Monte Carlo simulations.
| H01:β = 0 | H02:β = 1 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| k (i) |
 (ii) |
 (iii) |
 ADJ ADJ(iv) |
R2 (v) |
 (vi) |
tNW (vii) |
MSLNW (viii) |
tOLS (ix) |
MSLMC (x) |
MSLMC (xi) |
| 1 | −0.0026 | 0.30 | 0.39 | 0.01 | 0.00 | 0.61 | 0.272 | 0.61 | 0.239 | 0.378 |
| 2 | 0.0009 | 0.51 | 0.60 | 0.07 | 0.04 | 1.19 | 0.116 | 1.45 | 0.134 | 0.423 |
| 3 | −0.0006 | 0.51 | 0.58 | 0.11 | 0.06 | 1.52 | 0.064 | 1.83 | 0.132 | 0.437 |
| 4 | 0.0095 | 0.59 | 0.64 | 0.19 | 0.12 | 2.34 | 0.010 | 2.45 | 0.110 | 0.448 |
| 5 | 0.0190 | 0.64 | 0.65 | 0.22 | 0.14 | 2.84 | 0.002 | 2.63 | 0.122 | 0.457 |
| 6 | 0.0140 | 0.62 | 0.60 | 0.22 | 0.12 | 2.68 | 0.004 | 2.61 | 0.153 | 0.468 |
| 7 | 0.0110 | 0.62 | 0.59 | 0.22 | 0.10 | 2.63 | 0.004 | 2.56 | 0.181 | 0.484 |
| 8 | 0.0110 | 0.62 | 0.55 | 0.20 | 0.07 | 2.64 | 0.004 | 2.37 | 0.214 | 0.499 |
|
Note: Column (i) reports the forecast horizon, k, while columns
(ii), (iii) and (v) report the OLS coefficient
estimates, |
||||||||||
| H01:β = 0 | H02:β = 1 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| k (i) |
 (ii) |
 (iii) |
 ADJ ADJ(iv) |
R2 (v) |
 (vi) |
tNW (vii) |
MSLNW (viii) |
tOLS (ix) |
MSLMC (x) |
MSLMC (xi) |
| 1 | −0.0048 | 0.05 | 0.11 | 0.00 | −0.02 | 0.13 | 0.447 | 0.13 | 0.389 | 0.137 |
| 2 | −0.0011 | 0.41 | 0.48 | 0.06 | 0.03 | 1.26 | 0.104 | 1.34 | 0.129 | 0.191 |
| 3 | 0.0004 | 0.47 | 0.53 | 0.13 | 0.09 | 1.88 | 0.030 | 2.01 | 0.078 | 0.225 |
| 4 | 0.0140 | 0.59 | 0.64 | 0.24 | 0.19 | 3.06 | 0.001 | 2.87 | 0.046 | 0.256 |
| 5 | 0.0290 | 0.67 | 0.72 | 0.31 | 0.24 | 4.08 | 0.000 | 3.33 | 0.040 | 0.278 |
| 6 | 0.0340 | 0.69 | 0.73 | 0.35 | 0.27 | 4.25 | 0.000 | 3.60 | 0.042 | 0.308 |
| 7 | 0.0440 | 0.75 | 0.79 | 0.40 | 0.31 | 4.33 | 0.000 | 3.94 | 0.040 | 0.329 |
| 8 | 0.0580 | 0.80 | 0.83 | 0.41 | 0.32 | 4.73 | 0.000 | 3.94 | 0.050 | 0.341 |
|
Note: Column (i) reports the forecast horizon, k, while columns
(ii), (iii) and (v) report the OLS coefficient
estimates, |
||||||||||
We begin with results for model A. Table 5a shows that both the OLS coefficient estimate,  , and the
explanatory power of the regression, measured by R2, rises as the forecast
horizon is lengthened – a pattern suggesting that the explanatory power of model A rises
with forecast length. Unfortunately, however, this conclusion is premature. This pattern of
rising estimates for longer forecast horizons is not shared by
, and the
explanatory power of the regression, measured by R2, rises as the forecast
horizon is lengthened – a pattern suggesting that the explanatory power of model A rises
with forecast length. Unfortunately, however, this conclusion is premature. This pattern of
rising estimates for longer forecast horizons is not shared by  ADJ and
ADJ and  , implying that there is no clear
improvement in the explanatory power of model A as the horizon is lengthened.
, implying that there is no clear
improvement in the explanatory power of model A as the horizon is lengthened.
Turning to the null hypothesis H01: β = 0, Table 5a shows that the marginal significance levels derived from the Newey-West t-statistics, MSLNW, and from the Monte Carlo simulations, MSLMC, are often very different. The samples are apparently small enough to render the Newey-West asymptotic results extremely inaccurate. As a consequence, we must rely on the Monte Carlo evidence to assess the performance of the model. Based on this Monte Carlo evidence, at all forecast horizons, the null hypothesis H01: β = 0 cannot be rejected against the alternative β > 0, even at a 10 per cent level of significance. Model A cannot significantly outperform a random walk.
For model B, both the OLS coefficient estimate,  , and the regression
R2, rise as the forecast horizon is lengthened. This pattern is repeated by
, and the regression
R2, rise as the forecast horizon is lengthened. This pattern is repeated by
 ADJ
and R2ADJ, implying that the explanatory power of model
B does rise with forecast length; in contrast to the results for model A.
ADJ
and R2ADJ, implying that the explanatory power of model
B does rise with forecast length; in contrast to the results for model A.
As for model A, there is a substantial difference between the marginal significance levels for the null hypothesis, β = 0, based on Newey-West t-statistics and those based on the Monte Carlo simulations, again leading us to rely on the Monte Carlo results to derive inferences about model performance. These Monte Carlo results reveal a marked improvement in out-of-sample forecasting performance as the forecast horizon lengthens. Point estimates of β for one, two, and three-quarters-ahead forecasts, are positive, but insignificant. Over these shorter forecast horizons, model B cannot outperform a random walk.
The contrast with forecasts over time horizons longer than three quarters is striking. For these longer horizons, the out-of-sample forecasting performance improves considerably and the coefficient estimate of β is positive and significant at a five per cent level. Thus, model B contains significant information about future movements of the real exchange rate for horizons ranging from one to two years.
The results in Table 5b also show that the null hypothesis, H02: β = 1, cannot be rejected, implying that there is no evidence of bias in the model forecasts of the change in the real exchange rate.
Figure 3 shows the actual log changes in the real exchange rate against the expected changes from Model B, over one and two year horizons. The positive relationship between the expected and actual changes over each horizon emerges clearly from the figure.

4.2 Expected Excess Returns
We now turn to estimates of the one and two-year-ahead expected excess return to holding Australian bonds rather than a trade-weighted basket of foreign bonds.
Excess returns can be expressed either in terms of nominal appreciation and the nominal domestic/foreign interest differential, or real appreciation and the real interest differential. Using real variables, the excess return (in per cent) to holding a one-year (4-quarter) Australian dollar bond, ERt,4, is approximately:
where 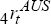 and
and
 are time-t
real interest rates on the domestic and trade-weighted foreign basket of one-year bonds, also in
per cent.
are time-t
real interest rates on the domestic and trade-weighted foreign basket of one-year bonds, also in
per cent.  is defined by:
is defined by:
where wj is the normalised country j trade weight, defined earlier,
and 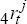 is
country j's real interest rate,
is
country j's real interest rate,  , where
, where 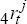 is the
one-year nominal interest rate and
is the
one-year nominal interest rate and  , the log consumer price index in
country j. The expected excess return on the Australian one-year bond,
Et(ERt4), is therefore:
, the log consumer price index in
country j. The expected excess return on the Australian one-year bond,
Et(ERt4), is therefore:
where we assume model B is used to generate the expectations  (qt+4−qt).
For all countries, we also make the simple assumption that the expected inflation rate from
period t to t+4 is equal to the most recently published annual inflation rate
available in quarter t, that is the inflation rate from period t−5 to
t−1, so that
(qt+4−qt).
For all countries, we also make the simple assumption that the expected inflation rate from
period t to t+4 is equal to the most recently published annual inflation rate
available in quarter t, that is the inflation rate from period t−5 to
t−1, so that  for country j.
for country j.
The two-year-ahead excess return, ERt8, in per cent is approximately:
where  and
and
 are the
time-t real interest rates in per cent per annum on the domestic and trade-weighted foreign basket of two-year bonds, with the latter
defined analogously to equation (11). For country j,
are the
time-t real interest rates in per cent per annum on the domestic and trade-weighted foreign basket of two-year bonds, with the latter
defined analogously to equation (11). For country j,  is
given by
is
given by  .
The expected excess return on the Australian two-year bond,
Et(ERt 8), is therefore approximately:
.
The expected excess return on the Australian two-year bond,
Et(ERt 8), is therefore approximately:
where model B is used to generate the real exchange rate expectations,  (qt+8 – qt), and
(qt+8 – qt), and  for each country
j.
for each country
j.
Figure 4 shows the levels of the terms of trade and the five-country trade-weighted Australian real exchange rate since the float. Also shown, over the period 1987:Q1 to 1994:Q2, are the one-year expected excess returns, Et (ERt,4 ), and the annualised two-year expected excess returns, AEt (ERt,8), defined by AEt (ERt,8) = Et (ERt,8) /2. Both these expected excess returns are highly variable over time and often large in magnitude. Thus, for example, the one-year expected excess return ranges from plus 13.2 per cent in 1987:Q4 to minus 19.7 per cent in 1991:Q2.

Both the size and variability of the expected excess returns is primarily due to large changes in Australia's expected real exchange rate, with little offset from the Australian-foreign expected real interest differential (see Figure 5 for a demonstration of this point for the one-year results). For both one and two-year expected returns, the correlation between the expected real exchange rate change and the expected real interest differential is negative but statistically insignificant.
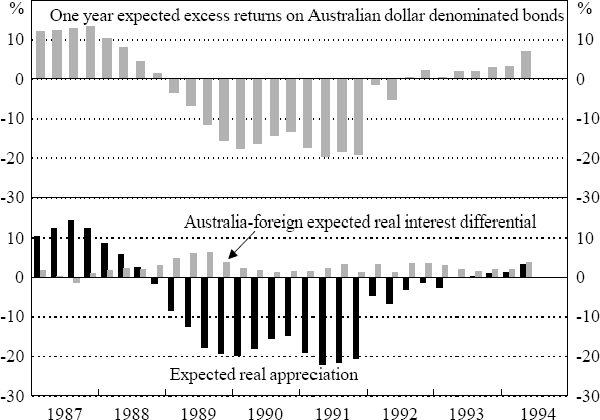
Figure 6 shows a comparison of actual and expected excess returns over both one and two year horizons. Given model B's capacity to predict real exchange rate changes over one and two-years, one might expect the model to have some predictive power for excess returns. As a formal test, we regress actual against expected excess returns to holding Australian dollar-denominated assets:

and present the results, as well as relevant hypothesis tests, in Table 6. As before, we report results based on both Newey-West t-statistics and Monte Carlo simulations.
| H01:β = 0 | H02:β = 1 | ||||||
|---|---|---|---|---|---|---|---|
| k (i) |
 (ii) |
 (iii) |
R2 (iv) |
tNW( ) )(v) |
MSLNW (vi) |
MSLMC (vii) |
MSLMC (viii) |
| 4 | 3.08 | 0.54 | 0.18 | 2.86 | 0.00 | 0.16 | 0.25 |
| 8 | 8.65 | 0.71 | 0.28 | 3.42 | 0.00 | 0.17 | 0.31 |
|
Note: Column (i) reports the forecast horizon, k, while columns
(ii), (iii) and (iv) report the OLS coefficient
estimates, |
|||||||
At both forecast horizons, the OLS coefficient estimate,  , is
positive and the equations have some explanatory power, judged by the R2.
The Newey-West t-statistics, tNW (
, is
positive and the equations have some explanatory power, judged by the R2.
The Newey-West t-statistics, tNW ( ),
suggest that the null hypothesis, H01: β = 0, can be rejected
against the alternative β > 0 at a one per cent significance level for both
forecast horizons (that is, MSLNW < 0.01). Again, however, the samples
are so small that we must discount these results and rely instead on the Monte Carlo results.
These results imply that the null hypothesis, H01: β = 0, can
be rejected against the alternative β > 0 at a significance level of only 16 or
17 per cent.
),
suggest that the null hypothesis, H01: β = 0, can be rejected
against the alternative β > 0 at a one per cent significance level for both
forecast horizons (that is, MSLNW < 0.01). Again, however, the samples
are so small that we must discount these results and rely instead on the Monte Carlo results.
These results imply that the null hypothesis, H01: β = 0, can
be rejected against the alternative β > 0 at a significance level of only 16 or
17 per cent.
While the estimated expected excess returns on Australian-dollar assets are often quite large in
magnitude (see Figure 4), the Monte Carlo results in Table 6 imply
that we can only have a moderate degree of confidence that these expected excess returns help to
predict actual excess returns. The small sample implies that the Monte-Carlo-estimated
distributions of the coefficient estimate, , are broad enough to
render statistical inference difficult. Only when a longer sample becomes available, will it be
possible to be more definitive.
, are broad enough to
render statistical inference difficult. Only when a longer sample becomes available, will it be
possible to be more definitive.
Footnotes
The seminal references are Meese and Rogoff (1983a, 1983b). See Frankel and Rose (1994) and Taylor (1995) for recent reviews on empirical exchange rate research. [6]
Expectations formed at the end of quarter t, Et, use all information available at the end of this quarter. While nominal exchange rates and interest rates are available, the period-t realisations of the terms of trade and domestic and foreign price levels are not. The period-t expectations Et tott and Et qt are therefore generated using terms of trade and real exchange rate models up to and including quarter t−1. [7]
A formal test of unbiasness also requires α = 0. [8]
One to eight-quarter-ahead forecasts are made in each period, 1987:Q1 to 1994:Q2 while the actual exchange rate data ends in 1994:Q4. Hence, the sample size for the equation (9) regressions is 30 for k = 1,2, but progressively less for forecasts further ahead (for k = 8, it is only 24). [9]








