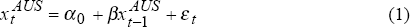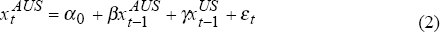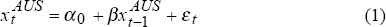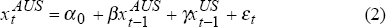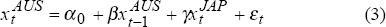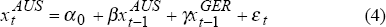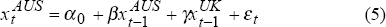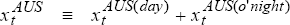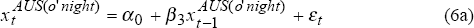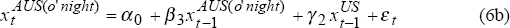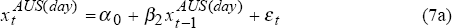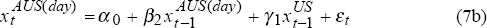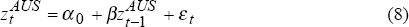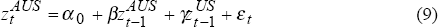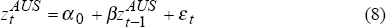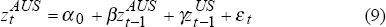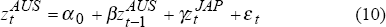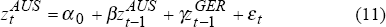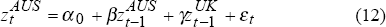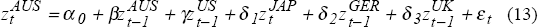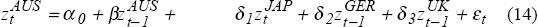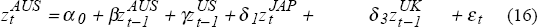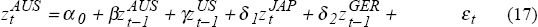RDP 9609: Australian Financial Market Volatility: An Exploration of Cross-Country and Cross-Market Linkages 3. Cross-Country Linkages
November 1996
- Download the Paper 777KB
In this section some econometric analysis is undertaken in order to investigate more rigorously the role of international factors in driving changes in Australia's key financial markets. We assess the extent to which developments in foreign bond and equity markets influence the size and direction of changes in the respective Australian counterpart markets.[10] The linkage between daily changes in Australian and foreign bond yields is examined first. This is followed by an investigation into the responsiveness of daily changes in Australian share prices to developments in major overseas stock markets.
3.1 Bond Markets
3.1.1 The Australian and US bond-market linkage
The examination undertaken in Section 2.1, was suggestive of an increased co-movement in the daily changes of Australian and US bond yields.
In order to further investigate this relationship, we estimate the following two simple equations:
where: 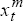 represent the daily ‘close-to-close’ basis point change in country m's
long bond yield.[11]
represent the daily ‘close-to-close’ basis point change in country m's
long bond yield.[11]
In order to obtain estimates of the dynamic profile of the US-Australia bond-market linkage, we run rolling regressions of equations (1) and (2) using daily observations from February 1987 to February 1996.[12] In these, and all subsequent rolling regressions we employ a 120-day (six-month) moving window, generating over 2,220 sets of estimates for each equation.
The results from these estimations are summarised in Figure 8. The increasing importance of the US bond market, in influencing the size and direction of movements in the Australian bond market from late 1993 onwards, is clearly illustrated by Figure 8.
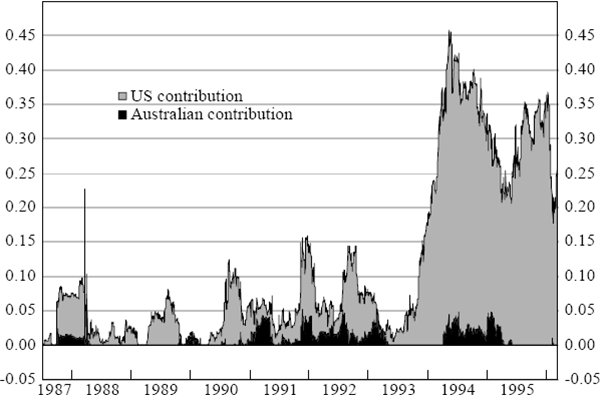
Figure 8 plots the adjusted coefficients of determination,  s from
rolling regressions (1) and (2) over the full sample. The darker shaded area, termed ‘Australian
Contribution’, is simply the
s from
rolling regressions (1) and (2) over the full sample. The darker shaded area, termed ‘Australian
Contribution’, is simply the  from regression (1), ie
from regression (1), ie  . The
lightly shaded area, denoted by ‘US Contribution’, is the
. The
lightly shaded area, denoted by ‘US Contribution’, is the 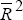 from equation (2) less the
from equation (2) less the 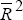 from equation (1), ie
from equation (1), ie 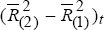 . This
represents the additional explanatory power provided by the inclusion of
. This
represents the additional explanatory power provided by the inclusion of 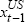 as a
regressor in the equation specification, and can be interpreted as reflecting the US market's
spillover effect on the Australian bond market.
as a
regressor in the equation specification, and can be interpreted as reflecting the US market's
spillover effect on the Australian bond market.
The most striking feature of Figure 8 is the rapid and substantial increase in the explanatory power of equation (2) since late 1993. A pronounced and sustained spillover effect from the US to Australian bond markets appears to exist in the last two years of the sample.
Specifically, Figure 8 reveals the following.
- The specification described by equation (1) provides little explanatory power over the entire sample period; the previous day's basis point change in Australian bond yields generally cannot account for any of the observed variation in current daily basis point changes in Australian yields.
-
Inclusion of
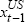 as an additional regressor leads to an increase in
explanatory power, although this improvement in goodness-of-fit displays considerable
variation over the period. Overnight (Australian time) US bond-market movements contribute
to explaining, at most, an additional 10 per cent of daily basis point changes in Australian
bond yields, over the period 1987 to end 1993. This contrasts with the last two years of the
sample period, 1994 and 1995, when US bond-market movements sometimes account for an
additional 45 per cent of the total variation in observed changes in Australian yields.
as an additional regressor leads to an increase in
explanatory power, although this improvement in goodness-of-fit displays considerable
variation over the period. Overnight (Australian time) US bond-market movements contribute
to explaining, at most, an additional 10 per cent of daily basis point changes in Australian
bond yields, over the period 1987 to end 1993. This contrasts with the last two years of the
sample period, 1994 and 1995, when US bond-market movements sometimes account for an
additional 45 per cent of the total variation in observed changes in Australian yields.
The increasing influence of the US bond market is also reflected in estimates of
coefficient γ on the regressor 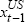 in equation (2), presented in
Figure 9. Daily basis point changes in Australian bond yields have clearly increased their
sensitivity to overnight changes in the US long bond yield, over the time period considered.
Especially noteworthy, is the sudden and apparently permanent increase in this coefficient
estimate since 1993. Over the period March 1993 to November 1994 the sensitivity of daily yield
changes in the Australian market to daily changes in US bond yields, records more than a
ten-fold increase, rising from 0.10 to around 1.
in equation (2), presented in
Figure 9. Daily basis point changes in Australian bond yields have clearly increased their
sensitivity to overnight changes in the US long bond yield, over the time period considered.
Especially noteworthy, is the sudden and apparently permanent increase in this coefficient
estimate since 1993. Over the period March 1993 to November 1994 the sensitivity of daily yield
changes in the Australian market to daily changes in US bond yields, records more than a
ten-fold increase, rising from 0.10 to around 1.
3.1.2 The influence of other foreign markets
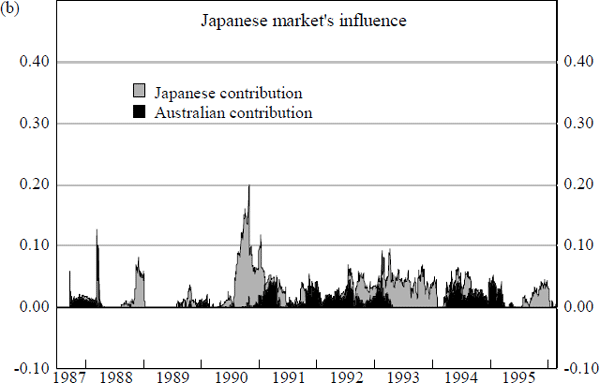
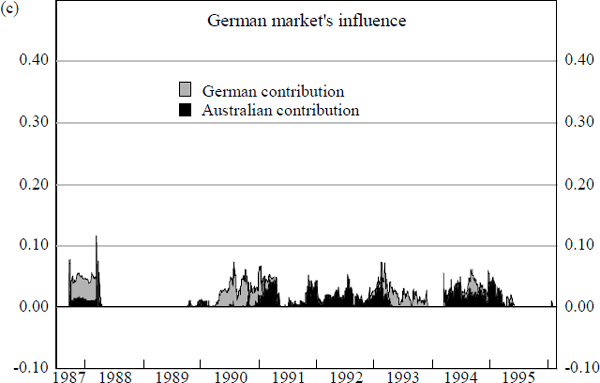
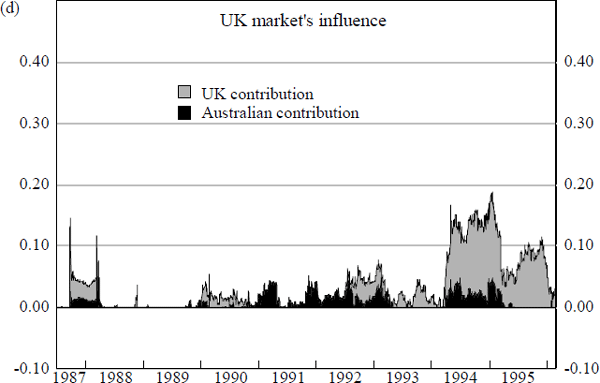
The question naturally arises as to whether other foreign bond markets also have similar spillover effects on the Australian market. Specifically we examine the relative importance of movements in the Japanese, German and UK bond markets in influencing the size and direction of daily changes in Australian bond yields.
The results from a series of estimations attempting to assess the relative influence of these other key bond markets are depicted in Figure 10. The charts in Figure 10 summarise rolling regression estimates of equations (1) to (5) displayed in Box 1 below:[13]
Box 1: The Relative Influence of Foreign Bond Markets
The relative importance of the US, Japanese, German and UK bond markets is measured by the increase in explanatory power resulting from the inclusion of the respective daily yield changes in these markets as an additional regressor to the autoregressive specification given by equation (1). Accordingly, for the charts appearing in Figure 10, we have the following definitions:
Australian Contribution ≡ 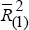 ; US
Contribution ≡
; US
Contribution ≡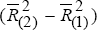 ;
;
Japanese Contribution ≡ 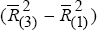 ; German
Contribution ≡
; German
Contribution ≡ 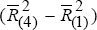 ;
;
UK Contribution ≡ 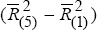 ;
;
where 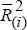 represents the adjusted coefficient of determination from regression i in Box 1.
represents the adjusted coefficient of determination from regression i in Box 1.
It is apparent from the charts in Figure 10 that the incremental contribution of the Japanese, German and UK bond market movements in explaining the daily basis point changes in Australian bond yields is negligible. The bulk of the increase in explanatory power can be attributable to movements in the US bond market. Spillover effects from the Japanese, German and UK markets, if any, are overwhelmingly dominated by spillover effects from overnight movements in US bond yields.[14] Additional econometric estimations reveal that the influence of these other foreign bond markets is reduced further when the US bond market's impact is explicitly allowed for in the equation specification.[15]
3.1.3 Overnight and intraday basis-point changes in Australian bond yields
The increasing influence of overnight changes in US bond yields upon the Australia bond market, can be further analysed by decomposing the daily changes in Australian bond yields into its overnight and intraday movements.
The daily (close-to-close) basis point change in Australian bond yields can be divided into an intraday (open-to-close) yield change and an overnight (close[t-1]-to-open) yield change:
where 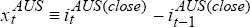 is
the daily basis-point change in yields,
is
the daily basis-point change in yields, 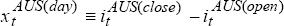 is the intraday change in
the Australian bond yield,
is the intraday change in
the Australian bond yield, 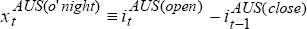 is the overnight change in the
Australian yield.
is the overnight change in the
Australian yield.
Examining the relative impact of US bond yield changes on these two components of the daily change in Australian yields, provides valuable insights into the informational efficiency of the Australian bond market.
If the developments overnight in the US bond market reflect the release of new information which is also pertinent to Australian bond yields, informational efficiency in the Australian market would dictate that this ‘news’ be fully incorporated in Australian opening prices or yields. That is, efficient processing of foreign information requires that such changes in US bond yields influence only the overnight change in Australian yields. Detection of an additional impact upon intraday changes in yields would, however, imply the presence of informational inefficiencies in the Australian bond market. Lagged responses by Australian bond market participants during the Australian trading day, possibly reflecting the effects of an initial over-reaction or under-reaction to the foreign market news, should not arise if the market is informationally efficient.
In order to examine this aspect of the Australian bond market the following sets of rolling regressions are estimated:
As in the cases above, the regressions employ a 120-day moving window. However the data which are used to construct the intraday and overnight yield changes derive from a different source, and extend only for the period January 1990 to February 1996.[16]
The differential impact of changes in US bond yields upon the overnight and intraday components of the daily change in Australian yields is clearly evident from Figures 11 and 12 below. Figure 11 is derived from regression estimates of equations (6a) and (6b), while Figure 12 summarise the results from rolling regressions (7a) and (7b).
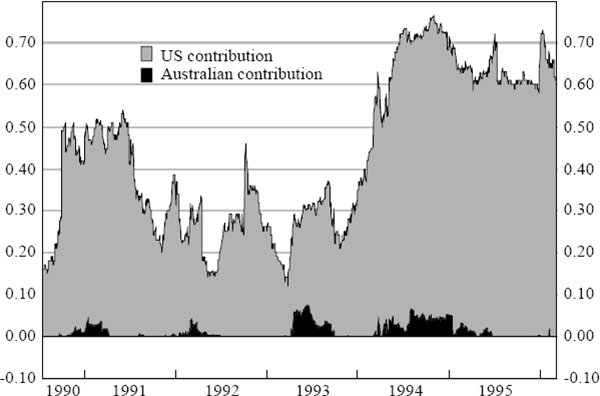
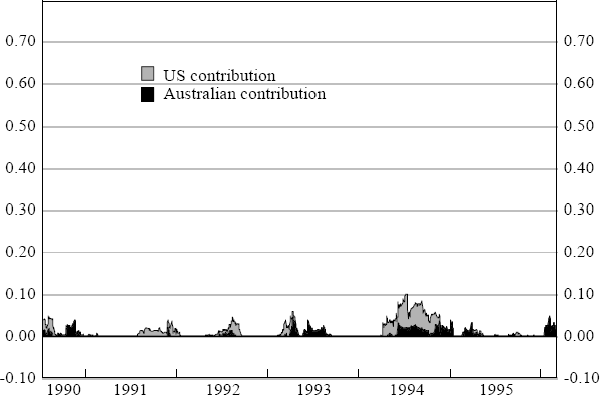
The differences between Figure 11 and Figure 12 are stark. They reveal that developments in the US bond market affect only the overnight component of the daily change in Australian yields, while having an insignificant influence on its intraday movement. Closer inspection of Figure 11, indicates that there have been six-monthly intervals in the period 1990 to 1996, where the daily change in US bond yields explains nearly 75 per cent of the observed variation in the overnight change in Australian yields. In contrast, the US market's contribution to explaining the intraday change in yields over the same period, fluctuates between −1 per cent and 5 per cent (see Figure 12).
Such a pattern, as indicated earlier, is consistent with informational efficiency in the Australian bond market. It also provides an interesting interpretation of the large US spillover effect documented in Figure 8 above. Starting in mid 1993, participants in the Australian bond market have interpreted developments in the US bond market as the release of new information increasingly relevant to the future course of Australian bond yields. However, why US bond yield movements should suddenly become intrinsically very pertinent to Australian yields, or alternatively, why they should suddenly be perceived by participants in the Australian bond market, as having greater relevance and importance to Australian bond yield movements, are 7two puzzling questions.
3.2 Share Markets
This section reports corresponding results on linkages between international equity markets. Using the same approach as shown in Section 3.1, we examine the relationship between daily percentage changes in the respective stock market indices.[17]
3.2.1 The Australian and US share-market linkage
The relationship between daily percentage changes in the Australian and US share market indices is investigated by running rolling regressions of the following two equations over the period February 1987 to February 1996:
where: 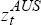 and
and 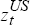 represent respectively the daily percentage change in the Australian and US share market
indices.
represent respectively the daily percentage change in the Australian and US share market
indices.
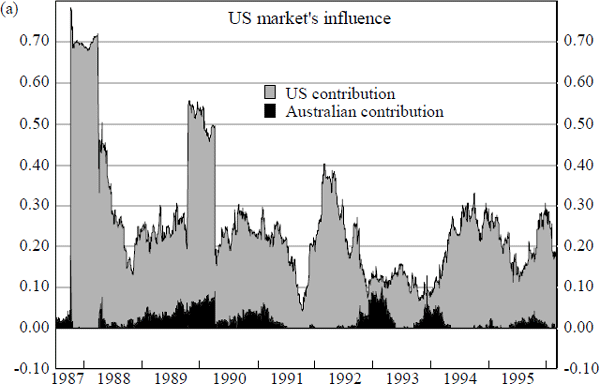
Plots of the time-varying 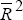 s from these two estimated equations are
contained in Figure 13 below.
s from these two estimated equations are
contained in Figure 13 below.
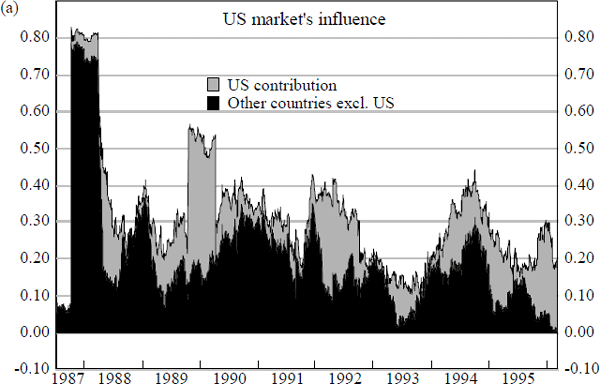
As with the situation for bond markets, developments in the US stock market appear to have a significant impact in determining the size and direction of daily changes in the Australian market. Figure 13 shows that a sizeable proportion of the observed daily percentages changes in the Australian share market index over the sample period can be accounted for by overnight movements in the US market. This is typically around 25 per cent, apart from some exceptional periods.
Differences are clearly evident however, when comparing the temporal profiles of the US bond and share markets' spillovers onto their respective counterpart Australian markets. Whereas the spillover from US to Australian bond markets is prominent only in the last two years, 1994 and 1995, the spillover from the US to the Australian stock markets is prevalent in a sizeable way throughout the entire sample period. The incremental contribution to explanatory power of daily changes in US stock prices, while variable, registers at least 20 to 30 per cent for most of the period. Although the US share-market spillover is slight in late 1991 and throughout 1993, it displays a very pronounced impact on Australian share-price movements during episodes of severe market turbulence such as the 1987 stock-market crash, the mini-collapse in 1989, and the bond market ‘sell-off’ of 1994.
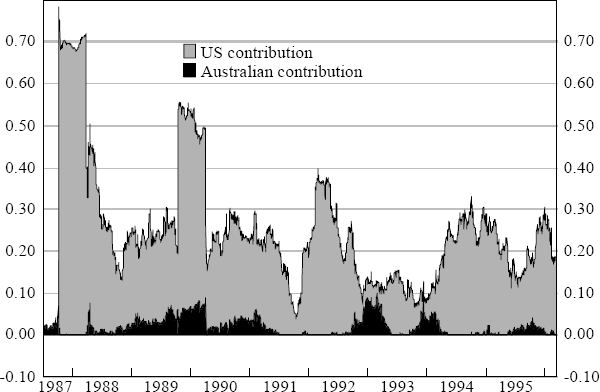
Such a pattern is also reflected in Figure 14, which shows how the Australian share market's responsiveness to daily changes in US share prices (the γ coefficient from equation (9)), varies over time.
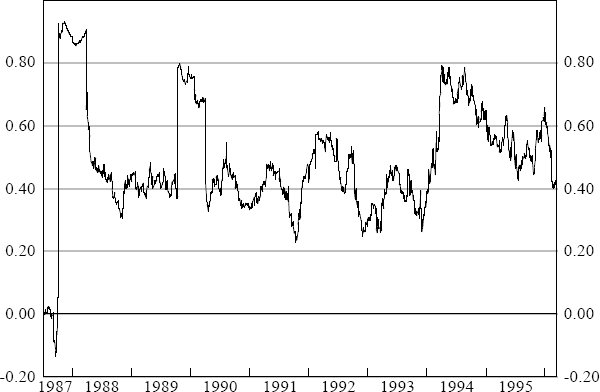
Figure 14 shows that for the most part, the Australian share market's elasticity with respect to developments in the US share market, fluctuates around 0.40. However, in periods of severe financial market turbulence, such as late 1987, late 1989 and early 1994, the Australian share price elasticity to overnight changes in US share prices doubled in size to 0.80. It is also worthwhile observing that Figure 16 does not reveal the presence of an upward trend in the Australian share market's sensitivity to daily changes in US share prices, unlike that documented by Figure 9 for daily changes in bond yields.
3.2.2 The influence of other foreign markets
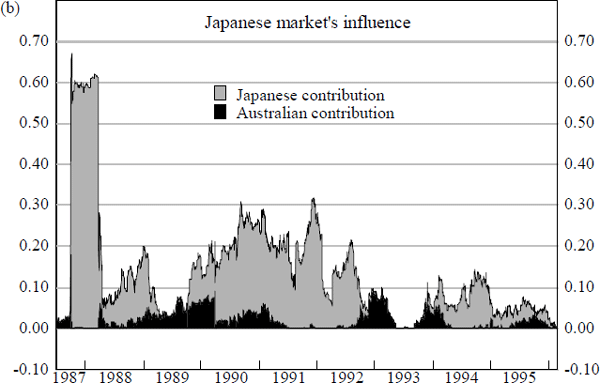
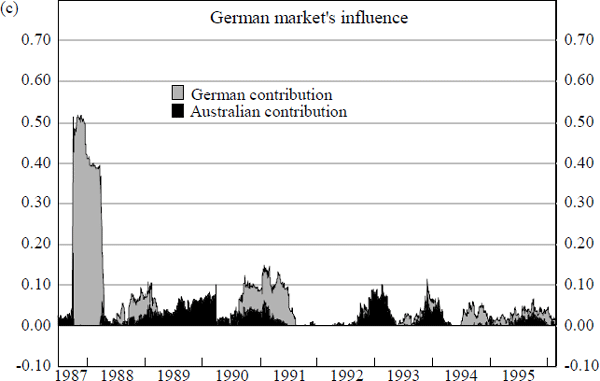
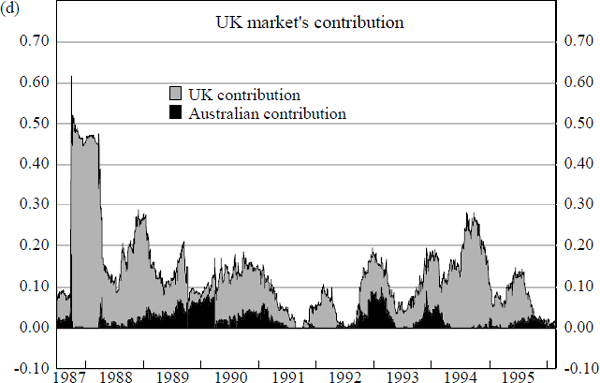
Results from estimations attempting to gauge the impact of other foreign share markets on the size and direction of daily changes in Australian share prices are summarised by Figure 15. These are derived from rolling regression estimates of the equations detailed in Box 2 below, and parallel those which are undertaken for bond markets.[18]
Box 2: The Relative Influence of Foreign Share Markets
The charts in Figure 15 reveal that the predominant foreign market influence on daily changes in Australian share prices is from the US share market. In contrast to the situation for the bond markets however, the US is not the only foreign market which has an impact on Australian share prices.
Chart (b) and Chart (d) of Figure 15 reveal instances of significant spillovers emanating from foreign share markets other than the US. Two main episodes can be identified. First, the period between mid 1990 and end 1992, when daily changes in Japanese share prices appear to have had a significant influence on Australian share prices, and second, the period between late 1992 and end 1994 when changes in UK share prices provide noticeable additions to explanatory power.
The above conclusions are reinforced by the charts in Figure 16. These summarise the results from estimation of the equations (13) to (17) detailed in Box 3 below and provide an alternative approach to assessing the relative importance of foreign equity markets. Each chart in Figure 16 provides a measure of a particular foreign market's contribution to explanatory power, over and above that which is provided by the combined contribution of all other foreign markets.[19]
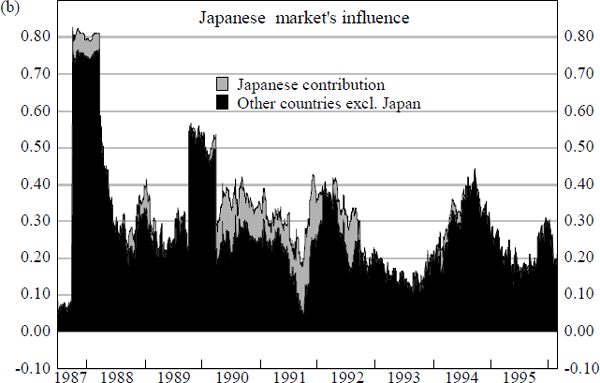
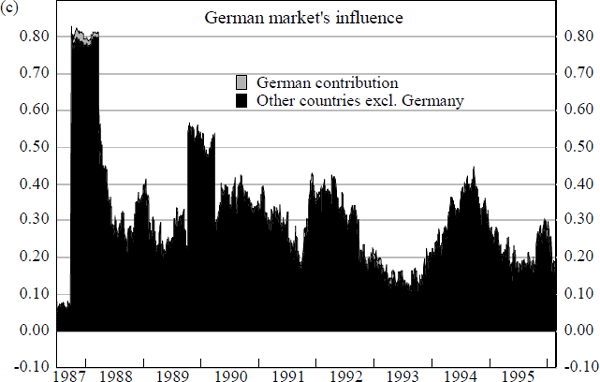
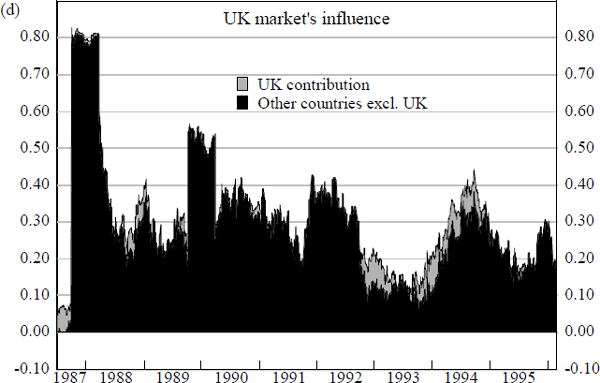
Box 3: The Relative Influence of Foreign Share Markets
Footnotes
Some literature on ‘spillover’ and ‘contagion’ effects already exists. Recent contributions focusing on spillover effects in equity markets include: Bertero and Mayer (1990), Eun and Shim (1989), Hamao, Masulis, and Ng (1990), King and Wadwhani (1990), Koch and Koch (1991), Lin and Ito (1994), Roll (1989), and von Furstenburg and Jeon (1989). With the exception of Borio and McCauley (1996) and some of the papers in Bank for International Settlements (1996), studies focussing on bond-market spillovers are comparatively few in number. [10]
The problem of data synchronisation, due to the presence of time zone differences
between the Australian and US markets, needs to be properly addressed. Since the United
States day t occurs after the Australian day t, equation (2) is
specified so that it is 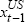 – the US day
t−1 basis point change in US long bonds – which appears as the
regressor in (2) rather than
– the US day
t−1 basis point change in US long bonds – which appears as the
regressor in (2) rather than 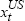 .
[11]
.
[11]
Standard OLS estimation will generate fixed parameter estimates, representing average values over the entire estimation period. Such a procedure will thus effectively mask any temporal changes that may occur in the relationship between the dependant and explanatory variables. Rolling regressions, on the other hand, estimated over such a sliding six-month window, will provide time-varying estimates of the relevant coefficients. This will highlight, as well as identify the timing of, any potential change that may occur in the relationship between the US and Australian bond markets. [12]
Data synchronisation, due to the presence of time-zone differences, dictates that the daily basis point change in German and UK bond yields along with that for the US, enter as a 1-day lagged regressor in the equations (ie indexed by t−1). Daily basis point changes in Japanese bond yields, however, enter as a contemporaneous (date t) regressor. [13]
Rolling regression estimates and analysis, similar in nature to that outlined in Sections 3.1.1 and 3.1.2, were also undertaken for (i) weekly basis point changes in bond yields and (ii) weekly averages of daily bond-market volatility. The results from these estimations were qualitatively similar to those identified for daily basis point changes. Evidence exists of sizeable spillovers from foreign bond markets, with developments in the US bond market being the predominant foreign market influence on the Australian bond market. [14]
We estimate (rolling regression) equations 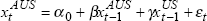 (a) and
(a) and 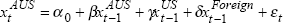 (b
), where the foreign bond markets incremental contribution to explanatory power is
defined by Other Foreign Bond Mkt.'s Contribution ≡
(b
), where the foreign bond markets incremental contribution to explanatory power is
defined by Other Foreign Bond Mkt.'s Contribution ≡ 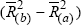 .
[15]
.
[15]
Daily opening quotes on Australian bond yields were unavailable from Datastream. For regressions (14) and (15) the intraday and overnight yield changes are constructed using Sydney Futures Exchange (SFE) data on opening and closing yields for Australian 10-year bond futures. [16]
The empirical examination detailed below is also undertaken for weekly percentage changes in the share market indices as well as for weekly averages of daily share-price volatility. The results from these investigations yielded conclusions qualitatively similar in nature to those found for daily percentage changes in share prices. [17]
For the charts in Figure 15, we have the following definitions: Australian
Contribution ≡ 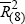 ; US Contribution ≡
; US Contribution ≡
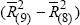 ;
Japanese Contribution ≡
;
Japanese Contribution ≡ 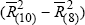 ; German
Contribution ≡
; German
Contribution ≡ 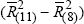 ; UK Contribution ≡
; UK Contribution ≡
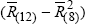 ;
where
;
where 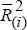 represents the adjusted coefficient of determination
from regression i in Box 2.
[18]
represents the adjusted coefficient of determination
from regression i in Box 2.
[18]
In Figure 16 Chart (a), we have the following definitions: US Contribution
(a) ≡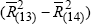 and All Other Countries Excluding
US ≡
and All Other Countries Excluding
US ≡ 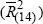 . Similarly in Chart (b) we have Japanese
Contribution (a) ≡
. Similarly in Chart (b) we have Japanese
Contribution (a) ≡ 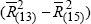 and All Other Countries
Excluding Japan ≡
and All Other Countries
Excluding Japan ≡ 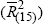 ; in Chart (c) German
Contribution (a) ≡
; in Chart (c) German
Contribution (a) ≡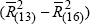 and All Other Countries
Excluding Germany ≡
and All Other Countries
Excluding Germany ≡ 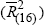 ; and in Chart (d) UK
Contribution (a) ≡
; and in Chart (d) UK
Contribution (a) ≡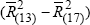 and All Other Counties
Excluding UK ≡
and All Other Counties
Excluding UK ≡ 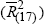 .
[19]
.
[19]