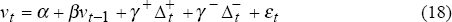RDP 9609: Australian Financial Market Volatility: An Exploration of Cross-Country and Cross-Market Linkages 5. Other Stylised Facts
November 1996
- Download the Paper 777KB
This section briefly examines two popular notions regarding volatility and market linkages. The first is that there is an asymmetry to volatility whereby ‘bad’ news causes more volatility than ‘good’ news. The second notion is that the strength of relationships between markets varies depending upon the state of the markets. In particular, the volatility in different markets is thought to be more correlated in periods of high volatility and during bear markets.
5.1 Asymmetry in Volatility
A common view held by many financial market observers is that there is an asymmetry or directionality to volatility: unanticipated price falls (‘bad news’) are believed to engender more volatility than equivalent unanticipated price rises (‘good news’).[22] This sub-section investigates that issue with respect to the Australian bond and share markets. Two questions are posed: is volatility, on average, higher during bear markets than during bull markets; and are market falls associated with greater volatility than rises of equal magnitude. Both questions receive positive answers. [23]
5.1.1 Is volatility higher during bear markets?
The relationship between volatility and the state of the market is examined by calculating the average volatility of bond and share markets during bull and bear markets. Bear (bull) markets are defined as extended periods of market falls (rises). The state of the market was identified by examining plots of market levels, using daily data, and picking the turning points. The results are shown in Figure 19. The shaded (unshaded) areas represent bear (bull) markets. The horizontal lines show the average volatility during the relevant period. It is apparent from the graphs that in general volatility was higher during bear markets.
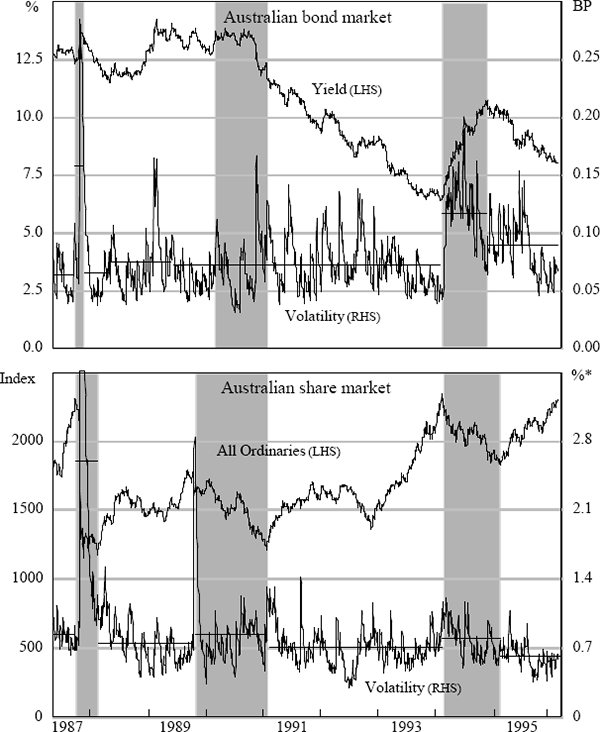
Note: *Scale has been truncated. During the October 1987 stock-market crash, daily Australian share-market volatility reached levels in excess of 9 per cent.
A difference-in-means test was performed where volatility was regressed against a constant and an additive dummy for bear markets. The dummy variable is significant at the 1 per cent level for both bond and share markets: there is a statistically significant difference between average volatility in bull and bear markets.[24] The difference in volatility depending on the state of the market seems to be more marked for shares, indicating that the asymmetry is more pronounced in that market.
Figure 19 also highlights the trends in volatility in each market. In the share market, which has a negative trend to its volatility, each bear (bull) market had lower volatility than the preceding bear (bull) market. Volatility fell from 102 per cent of its whole-sample average in the 1990 bear market, to 96 per cent in the 1994 bear market. In the bull markets, it fell from 85 per cent in 1991–1993 to 74 per cent in 1995. In contrast, in the bond market, which has a positive trend, each bull market had higher volatility than did its predecessor. Volatility was 87 per cent of its whole-sample average in the 1990–93 bull market and 107 per cent in 1995.
5.1.2 Do market falls cause greater volatility than market rises?
To investigate whether or not market falls cause greater volatility than market rises, the following equation was estimated for the bond and share markets:
where: vt is the volatility at time t, 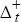 is the absolute value of a market rise and
is the absolute value of a market rise and 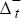 is the absolute value of
a market fall at time t. Obviously
is the absolute value of
a market fall at time t. Obviously 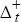 and
and 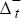 are
mutually exclusive. For bonds, market movements are measured by the basis point change in
yields; for the share market the percentage change in the All Ordinaries index is used.
are
mutually exclusive. For bonds, market movements are measured by the basis point change in
yields; for the share market the percentage change in the All Ordinaries index is used.
Two sets of equations were estimated for each market. In the first, weekly averages of daily data were used in the regressions. In the second set, market changes were given by the weekly (Friday-to-Friday) change in the market level. Weekly averages of daily data were again used for volatility. To allow for the high degree of persistence in volatility, the equations were estimated using robust errors.
If an asymmetry exists, the coefficients of the market change variables will be different. In particular, γ− will be greater than γ+ if market falls are associated with higher volatility than market rises. The results are recorded in Table 4. They provide support for the thesis that market falls cause higher volatility.
| Market |
Constant α |
Lagged volatility νt−1 |
Market rise γ+ |
Market rise γ− |
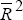 |
|---|---|---|---|---|---|
| Bond | |||||
| Δweekly average | 0.01** (0.00) |
0.82*** (0.03) |
0.28*** (0.04) |
0.39*** (0.09) |
0.78 |
| Weekly change | 0.01** (0.00) |
0.82*** (0.02) |
0.06*** (0.01) |
0.08*** (0.01) |
0.78 |
| Share | |||||
| Δweekly average | 0.03* (0.02) |
0.74*** (0.02) |
0.36*** (0.06) |
0.75*** (0.12) |
0.93 |
| Weekly change | 0.03* (0.02) |
0.74*** (0.02) |
0.07*** (0.01) |
0.15*** (0.02) |
0.93 |
|
Notes: (a) Standard errors robust to serial correlation and heteroscedasticity
are presented in parentheses below the coefficient estimates. |
|||||
The coefficients for market falls are clearly greater than those for market rises.[25] The difference in the coefficients is stronger for shares than for bonds, with the market fall coefficient more than twice the market rise coefficient. This supports the observation, noted above, that the asymmetry is stronger in the share market than in the bond market. For both markets one may conclude that there is an asymmetry in the response of volatility to market movements, with falls being associated with higher volatility than rises.
5.2 Asymmetry in Market Linkages
Previous parts of this paper have investigated the linkages between markets, in terms of both their volatility and the movements of their levels. This section addresses the issue of whether asymmetries exist in such linkages. Specifically, it considers three questions. The first is whether volatility is more correlated in periods of high volatility than in periods of low volatility. Secondly, are market movements more correlated in bear markets than in bull markets? Finally, is volatility more correlated in bear markets than in bull markets?
Semi-correlations are used to determine whether correlations differ depending upon the level of volatility or market movements. Semi-correlations measure the correlation of two series in three states of the world: up-up (both series are above their means), down-down (both series are below their means) and mixed (one series is above its mean and the other is below).[26] There is no statistical reason why above average volatility or market movements should have a different correlation from those below the mean. Thus, different correlations in the up-up and down-down states indicate an asymmetry in the relationship.
5.2.1 Is volatility more correlated in periods of high volatility?
Table 5 contains the semi-correlations of volatility in Australian and US markets. Seventeen of the 21 relationships have stronger correlations in the ‘up-up’ markets. This is cogent evidence that the correlation of volatility across markets is stronger during periods of above average volatility. Some of the differences between correlations in the two states are very dramatic. In particular, the relationships between share and bond markets, both within each country and internationally, show a marked asymmetry in correlations.
| Asset pair |
Up-up correlation | Down-down correlation | Mixed correlation | Total correlation |
|---|---|---|---|---|
| Intra-Australian markets | ||||
| Share-bond | 0.77 | −0.11 | −0.53 | 0.50 |
| Share-US$/$A | −0.35 | 0.12 | −0.56 | 0.25 |
| Share-TWI | 0.25 | 0.17 | −0.33 | 0.21 |
| Bond-TWI | 0.32 | 0.22 | −0.56 | 0.36 |
| Bond-US$/$A | 0.25 | −0.10 | −0.59 | 0.18 |
| TWI-US$/$A | 0.67 | 0.29 | −0.49 | 0.64 |
| Intra-US markets | ||||
| Share-bond | 0.77 | 0.12 | 0.50 | 0.67 |
| Share-Yen/US$ | 0.81 | −0.02 | −0.59 | 0.12 |
| Bond-Yen/US$ | 0.025 | 0.11 | −0.53 | 0.18 |
| Inter-country markets | ||||
| Share(US)-Share(A) | 0.95 | 0.07 | −0.29 | 0.92 |
| Share(US)-Bond(A) | 0.98 | 0.00 | −0.57 | 0.39 |
| Share(US)-US$/$A | 0.11 | −0.04 | −0.47 | 0.25 |
| Share(US)-TWI | 0.31 | −0.18 | −0.38 | 0.11 |
| Bond(US)-Share(A) | 0.73 | 0.07 | −0.53 | 0.64 |
| Bond(US)-Bond(A) | 0.63 | −0.33 | −0.58 | 0.45 |
| Bond(US)-US$/$A | 0.33 | 0.11 | −0.45 | 0.37 |
| Bond(US)-TWI | 0.24 | 0.37 | −0.48 | 0.17 |
| Yen/US$-Share(A) | −0.037 | 0.05 | −0.47 | 0.10 |
| Yen/US$-Bond(A) | −0.16 | 0.013 | −0.58 | 0.07 |
| Yen/US$-US$/$A | 0.046 | 0.22 | −0.44 | 0.22 |
| Yen/US$-TWI | 0.16 | 0.09 | −0.56 | 0.28 |
|
Notes: The semi-correlations measure the correlation of volatility in three states of the world: up-up (volatility in both markets is above the mean), down-down (volatility in both markets is below the mean) and mixed (one market's volatility is above the mean, the other below). Correlations are calculated from weekly averages of daily data. The sample is for week-ending 15/5/87 to week-ending 2/2/96. |
||||
The asymmetry appears to be weak for foreign exchange markets. The correlation difference is generally low for relationships including an exchange rate. The four relationships which have stronger correlations in down-down markets all involve exchange rates. Given the unusual status of exchange rates this is perhaps not surprising. The relationships between asset (ie bond and share) markets uniformly have stronger correlations in the up-up state of the world.
5.2.2 Are market movements more correlated in bear markets?
Table 6 contains the semi-correlations of changes in market levels in Australian and US markets. Twelve of the 21 relationships have stronger correlations in the down-down markets, nine in the up-up markets. This does not indicate any systematic asymmetry in the relationships. It is, however, notable that all of the intra-Australia relationships have stronger correlations in the down-down markets. In Australia at least, it may be that markets do show greater co-movement in bear markets.
| Asset pair |
Up-up correlation | Down-down correlation | Mixed correlation | Total correlation |
|---|---|---|---|---|
| Intra-Australian markets | ||||
| Share-bond | −0.09 | −0.28 | 0.56 | −0.35 |
| Share-US$/$A | −0.03 | 0.21 | −0.60 | 0.14 |
| Share-TWI | 0.08 | 0.20 | −0.61 | 0.12 |
| Bond-TWI | −0.19 | −0.27 | 0.56 | −0.11 |
| Bond-US$/$A | 0.05 | −0.16 | 0.56 | −0.16 |
| TWI-US$/$A | 0.48 | 0.78 | −0.52 | 0.77 |
| Intra-US markets | ||||
| Share-bond | −0.19 | −0.32 | 0.75 | −0.13 |
| Share-Yen/US$ | 0.21 | 0.03 | −0.53 | 0.09 |
| Bond-Yen/US$ | −0.16 | 0.10 | 0.52 | 0.02 |
| Inter-country markets | ||||
| Share(US)-Share(A) | 0.06 | 0.62 | −0.55 | 0.37 |
| Share(US)-Bond(A) | −0.12 | −0.07 | 0.55 | −0.16 |
| Share(US)-US$/$A | 0.03 | 0.10 | −0.62 | −0.07 |
| Share(US)-TWI | −0.10 | 0.01 | −0.61 | −0.02 |
| Bond(US)-Share(A) | 0.01 | −0.04 | 0.73 | 0.26 |
| Bond(US)-Bond(A) | 0.15 | 0.14 | −0.59 | 0.19 |
| Bond(US)-US$/$A | −0.19 | 0.06 | 0.52 | 0.09 |
| Bond(US)-TWI | −0.05 | −0.04 | 0.50 | 0.05 |
| Yen/US$-Share(A) | −0.09 | 0.00 | −0.61 | 0.03 |
| Yen/US$-Bond(A) | −0.08 | −0.01 | 0.55 | 0.03 |
| Yen/US$-US$/$A | 0.07 | 0.24 | −0.65 | −0.06 |
| Yen/US$-TWI | 0.22 | 0.23 | −0.55 | 0.33 |
|
Notes: The semi-correlations measure the correlation of changes in market levels in three states of the world: up-up (the change in market levels in both markets is above the mean), down-down (the change in levels in both markets is below the mean) and mixed (one market's change in level is above the mean, the other below). The change in market level is measured by the daily percentage change in the relevant share index or exchange rate. For bonds, the daily basis point change is used. Correlations are calculated from weekly averages of daily data. The sample is for week-ending 15/5/87 to week-ending 2/2/96. |
||||
In general the results do not show large disparities between correlations in the two states. The largest difference is for share(US)-share(Australia), and this result is probably heavily influenced by the 1987 stock-market crash. Those relationships with stronger correlations in bull markets do not provide significant evidence of an asymmetry in favour of bull markets as they generally involve movements around near-zero correlation. The share(US)-yen and bond(US)-US$/$A relationships are exceptions, as they both have significant levels of correlation in the up-up markets. An interesting result is that for the bond(US)-bond(Australia) relationship. It shows effectively no change in correlation for the different states.
5.2.3 Is volatility more correlated in bear markets?
Table 7 reports the correlations of volatility depending upon the state of market movements. Note that it takes a slightly different approach to that in Table 5, as it uses market movements to define the up-up, down-down and mixed states, not the state of volatility.
| Asset pair |
Up-up correlation | Down-down correlation | Mixed correlation | Total correlation |
|---|---|---|---|---|
| Intra-Australian markets | ||||
| Share-bond | 0.44 | 0.53 | 0.50 | 0.50 |
| Share-US$/$A | 0.27 | 0.23 | 0.28 | 0.25 |
| Share-TWI | 0.21 | 0.26 | 0.19 | 0.21 |
| Bond-TWI | 0.40 | 0.24 | 0.41 | 0.36 |
| Bond-US$/$A | 0.37 | 0.16 | 0.04 | 0.18 |
| TWI-US$/$A | 0.52 | 0.73 | 0.67 | 0.64 |
| Intra-US markets | ||||
| Share-Bond | 0.39 | 0.86 | 0.62 | 0.67 |
| Share-Yen/US$ | 0.24 | 0.14 | 0.09 | 0.12 |
| Bond-Yen/US$ | 0.15 | 0.18 | 0.19 | 0.18 |
| Inter-country markets | ||||
| Share(US)-Share(A) | 0.67 | 0.94 | 0.94 | 0.92 |
| Share(US)-Bond(A) | 0.41 | 0.60 | 0.26 | 0.39 |
| Share(US)-US$/$A | 0.19 | 0.08 | 0.33 | 0.25 |
| Share(US)-TWI | −0.15 | 0.11 | 0.19 | 0.11 |
| Bond(US)-Share(A) | 0.46 | 0.84 | 0.32 | 0.64 |
| Bond(US)-Bond(A) | 0.24 | 0.55 | 0.52 | 0.45 |
| Bond(US)-US$/$A | 0.44 | 0.33 | 0.36 | 0.37 |
| Bond(US)-TWI | 0.20 | 0.26 | 0.05 | 0.17 |
| Yen/US$-Share(A) | −0.01 | 0.14 | 0.15 | 0.10 |
| Yen/US$-Bond(A) | 0.08 | 0.06 | 0.05 | 0.07 |
| Yen/US$-US$/$A | 0.20 | 0.26 | 0.22 | 0.22 |
| Yen/US$-TWI | 0.21 | 0.42 | 0.20 | 0.28 |
|
Notes: The correlations measure the correlation of volatility in three states of the world: up-up (the change in market levels in both markets is above the mean), down-down (the change in levels in both markets is below the mean) and mixed (one market's change in level is above the mean, the other below). The change in market level is measured by the daily percentage change in the relevant share index or exchange rate. For bonds, the daily basis point change is used. Correlations are calculated from weekly averages of daily data. The sample is for week-ending 15/5/87 to week-ending 2/2/96. |
||||
Thirteen of the 21 relationships are stronger in the down-down, or bear, markets. This provides some suggestion of a tendency for volatility to be more correlated in bear markets, but the evidence is neither universal nor overly strong.
Again, all of the eight relationships which have stronger correlations in the up-up, or bull, markets involve exchange rates. The other seven relationships involving exchange rates have stronger correlations in the down-down markets. This indicates that no asymmetry exists in the foreign exchange markets. As mentioned above, given the unusual status of exchange rates and the difficulty of defining bull and bear markets with respect to them, this is not a surprising result.
An alternative view of these results is that bond and share markets are characterised by an asymmetry in their volatility correlations. Every combination involving only bond and share markets (ie any relationship not involving an exchange rate) has stronger volatility correlations in bear markets. Of course, to the extent that bear markets are associated with higher than usual volatility, this result replicates the first finding that volatility is more correlated in periods of high volatility. Some of the differences in correlation are marked. For example, see the share(US)-bond(US), bond(US)-share(Australia) and bond(US)-bond(Australia) relationships.
Footnotes
This feature of directionality or asymmetry in volatility, which is also sometimes referred to in the literature as the ‘leverage effect’, was first noted by Black (1976). [22]
The approach follows closely that which is adopted by Borio and McCauley (1996), in Annex III pp. 90–98. [23]
The difference-in-means test does not take into account the persistent nature of volatility. Tests allowing for this autoregressive aspect of volatility would be required before one could conclude with any certainty that bear markets generate greater volatility than bull markets. [24]
The null hypothesis that γ− equals γ+ is rejected at the 1% level for both the bond and share markets. [25]
See Erb, Harvey and Viskanta (1994). [26]