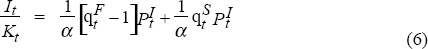RDP 9610: Share Prices and Investment 2. Share Prices and Investment – Some Theory

The theoretical linkages between share prices and investment have been well documented.^[2] In neoclassical investment theory, a manager chooses combinations of capital and labour (subject to certain constraints) in order to maximise the value of the firm.^[3] Even if the cost of an additional unit of capital is known in advance, the revenue that the capital is likely to generate over its lifetime is not known with any certainty. Managers have to make an assessment of the likely future profits that the increment to the capital stock will generate, discounted at some appropriate rate, and contrast it with the marginal cost of capital to determine whether the investment should go ahead:

where I is investment, K is the capital stock, E{ø} is the discounted present value of the revenue expected to be generated by the additional unit of capital, P^I is the marginal cost of capital and α is the cost of adjusting the existing capital stock.^[4]

A similar framework can be used to calculate the value of the firm. The fundamental value of the firm (V) is equal to the discounted present value of the cash flow stream that the existing capital stock is expected to generate:

Thus, the same types of expectational variables that determine the investment decision also determine the value of the firm (the firm's share price). This relationship was recognised by Tobin (1969) in the ‘q’ theory of investment where q is defined as the ratio of the market value of the firm to the replacement cost of its existing capital stock:

Combining Equations (1) to (3) illustrates the basic relationship between investment and Tobin's q:^[5]

Equation (4) illustrates that when the market value of capital exceeds its replacement cost (q>1), a firm is able to increase its value by investing. Further, as the dominant source of variation in q comes from the numerator – the market value of the firm – the equation also illustrates that investment is related to real share prices ().^[6]

As discussed in the introduction, however, there is a body of literature which suggests that a firm's share price incorporates speculative factors unrelated to the value of the firm. In essence, the fundamental value of the firm can be expressed as its market value less its speculative value:

Given the existence of speculative and fundamental elements to a firm's share price, the q investment model (Equation (4)) can be rewritten as:

As such, Equation (6) provides the theoretical framework by which we can test whether speculative share-price movements distort investment decisions. A form of this relationship is tested in Section 4. As a preliminary to examining the relationship between real share prices and investment, we first examine the extent to which inefficiencies in share prices can be identified.

Footnotes

See Barro (1990), Blanchard et al. (1990), Morck et al. (1990), Chirinko (1993) and Tease (1993). [2]

For a survey of neoclassical investment theory see Chirinko (1993). [3]

In a more general model, the purchase cost (P^I) may not be entirely known in advance. Future training and maintenance costs could be represented by a discounted sum, analogous to ø. [4]

In theory, investment should be related to ‘marginal q’ (the ratio of the discounted future revenues from an additional unit of capital to its purchase price). However, as marginal q is unobservable, empirical research has tended to use ‘average q’ as reflected, for example, in the stock market valuation of the firm. The distinction between average and marginal q is discussed in Hayashi (1982). This distinction highlights a problem in using average q measures in empirical tests of the theory. For example, an energy price shock would reduce the value of the existing capital stock but would encourage energy conserving investment: average q would fall while marginal q would rise (see Blanchard et al. 1990, p. 7). While the distinction between average and marginal q is not examined in this paper, Chirinko (1993), among others, has shown that the relationship is: marginal q = (average q – 1) P^I. [5]

See Barro (1990). [6]