RDP 9801: Labour Market Adjustment: Evidence on Interstate Labour Mobility Appendix B: VAR Results and Sensitivity Analysis
February 1998
- Download the Paper 314KB
The two tables below present summarised results from the two VAR models in Section 5 of the paper. In the tables, the first number quoted is the sum of the lag coefficients, the second number is the p-value for the F-test that the lags are jointly significant. These tables are followed by discussion of sensitivity analysis conducted on the two models.
| Equation | |||
|---|---|---|---|
| LHS variable: | Change in employment (Δem) |
Unemployment rate (ur) |
Participation rate (pr) |
| Change in employment (Δem) | 2.02 [0.00] |
0.16 [0.00] |
0.29 [0.00] |
| Unemployment rate (ur) | −0.28 [0.00] |
0.85 [0.00] |
0.13 [0.00] |
| Participation rate (pr) | −0.45 [0.00] |
0.07 [0.00] |
0.90 [0.00] |
 |
0.25 | 0.87 | 0.99 |
| LHS variable: | Change in employment (Δem) |
Unemployment rate (ur) |
Participation rate (pr) |
Change in average weekly earnings (Δwage) |
|---|---|---|---|---|
| Change in employment (Δem) | 2.28 [0.00] |
0.36 [0.00] |
−0.03 [0.00] |
−1.17 [0.00] |
| Unemployment rate (ur) | −0.05 [0.00] |
0.87 [0.00] |
0.12 [0.00] |
−0.01 [0.27] |
| Participation rate (pr) | −0.26 [0.00] |
0.04 [0.19] |
0.94 [0.00] |
0.13 [0.10] |
| Change in average weekly earnings (Δwage) | 0.11 [0.52] |
−0.04 [0.00] |
0.01 [0.01] |
−0.92 [0.00] |
 |
0.30 | 0.92 | 0.99 | 0.09 |
These models were then subject to a range of sensitivity tests to examine the robustness of conclusions from the VAR model. Firstly, to gauge whether the propensity to migrate has become more pronounced over time, the sample was split into two equal sub-samples, and the migration response estimated for each sub-sample using the four-variable model.
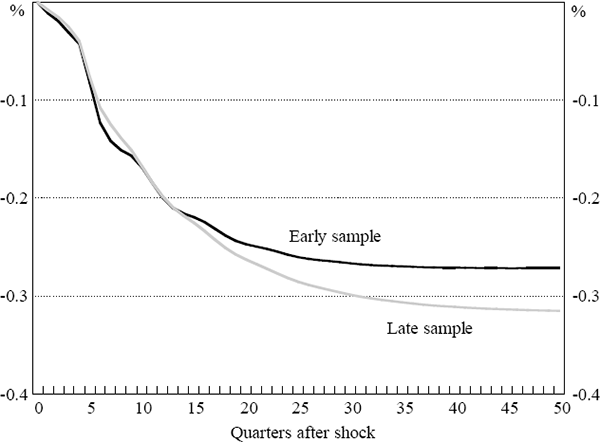
The results of this exercise are shown in Figure B1, and provide some, albeit limited, support for the view that the Australian workforce has become more geographically mobile over the sample period. The long-run migration response in the second half of the sample suggests that an initial negative shock to employment of 10 workers results in long-run net out-migration of 3.2 workers, compared to 2.7 workers in the first half of the sample. The difference between these figures was not, however, statistically significant at the 10 per cent level based on the bootstrapped standard errors. In addition, the speed of the migration response was very similar between the two sub-samples. The larger migration flows and the higher standard deviation of the state unemployment rates reported in Figure 5 in more recent times may also indicate that there have been larger state-specific shocks in the latter part of the sample.
Given that the unit root tests were not altogether conclusive for several variables, we investigate the sensitivity of the impulse response functions to alternative model specifications. These include:
- modelling the relative wage as I(0);
- changing the lag length to three, nine and twelve quarters;
- excluding the ACT and Northern Territory from the panel as both of these have relatively low population bases and correspondingly lower data quality;
- estimating the VAR with the employment share em as I(0); and
- treating the relative unemployment rate ur as I(1), rather than I(0).
Figure B2 presents sensitivity bounds for the projected migration response from the shock. We obtain this by ranking the migration responses under each combination of the specification changes in ascending order,[17] and taking a two-tailed 90 per cent ‘sensitivity interval’ of the migration response based on this distribution. This approach, in the spirit of Leamer and Leonard (1983), provides a concise way of summarising the effect of specification changes on the model's main results.
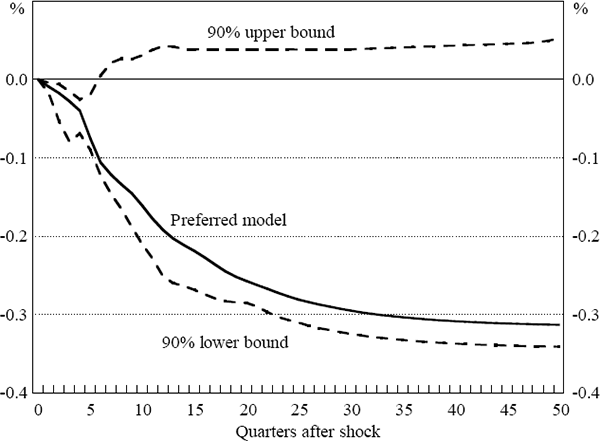
The key results are generally robust to the changes in specification listed above. In a number of cases where the employment share is specified in levels, the model was not dynamically stable (implying that the migration path after a shock does not settle down to a long-run value, but instead explodes). This provides further evidence that the employment share is best modelled as being non-stationary. This result aside, Figure B2 suggests that the results in the model are robust to a wide range of specification changes. Two main results stand out. Firstly, decreased labour demand nearly always seems to induce out-migration (although the lower bound of the long-run migration response is actually below zero). Secondly, the upper bound on the migration effect is only 0.35, much less than Blanchard and Katz's (1992) estimate of 1.3 for the US economy.
Blanchard and Katz's estimates are based on a model using annual data, while our model uses quarterly data. As a further sensitivity test, we re-estimate the four-variable model with annual data. The long-run employment response is higher than that for the quarterly model, and is between 0.4 and 0.65 depending on the lag length used (we experimented with lag lengths between one and four). The duration of the adjustment period is also longer than in the quarterly model, implying that migration acts less quickly to equalise labour market conditions than in the quarterly model. We prefer the quarterly specification because it employs all the available information, which the annual model does not. However, we do note that our results are relatively sensitive to changing the periodicity of the data.
As a final robustness test, the model is re-estimated excluding each of the states in turn. Although this results in some variation in the impulse response functions for each variable, the main inferences from the model are not affected by the exclusion of any particular state.
Footnote
There are 24 × 4 = 64 specification combinations in total. [17]