RDP 9801: Labour Market Adjustment: Evidence on Interstate Labour Mobility 5. Dynamics of State Labour Market Adjustment

In the above discussion we have paid little attention to the actual dynamics of migration flows in response to factors that adversely affect employment in a particular state. In this section we address this issue using a VAR model of the state labour markets that incorporates information on state employment, unemployment and participation rates. The model is based on Blanchard and Katz (1992), and although it does not explicitly incorporate net migration, an estimate of migration flows can be backed out of the model based on the time paths of the other variables.

We use monthly data on employment, the labour force and population for the states and territories as the basis of our empirical work. From this data, we construct three labour market variables. The first variable is (the natural logarithm of) employment in the state as a proportion of total employment. The second variable compares the unemployment rate in the state to the national unemployment rate. It is actually defined as the log ratio of the state and national ‘employment rates’ (where the employment rate is one minus the unemployment rate). This definition is consistent with the equivalent variables defined in Blanchard and Katz, and Decressin and Fatas (1995).^[9] The third variable is a log ratio of the state participation rate to the national participation rate.

In each case, the variable is a ratio between the state and national levels and is thus a measure of the relative performance of the state. The variables are defined in this way because it is differences between labour market conditions across states (such as unemployment rate differentials) that should encourage the movement of labour between states.

The actual definitions of the variables are:

The exact specification of the model chosen is dependent upon the time series properties of the variables. In Blanchard and Katz, the employment share (em) is treated as integrated of order 1 (I(1)) and first differenced, while the other two variables are modelled in levels. We conduct two tests to investigate whether this specification is consistent with the Australian empirical evidence on the persistence of the three variables. Firstly, we apply a panel unit root test on each variable across all the states. Secondly, we conduct univariate unit root tests on each variable for each state. Results of both tests are presented in Appendix A.

From the panel unit root tests, the employment share (em) is I(1) (although it is possible to reject the null of non-stationarity at the 10 per cent level), while the unemployment rate and participation rate are both stationary at the 1 per cent level of significance. However, the unit root tests on the individual series often produce contradictory results for the same variable. The employment share is found to be I(1) in seven cases, but stationary in Tasmania. Results for the relative unemployment rate imply a stationary relative unemployment rate in four cases (South Australia, Tasmania, ACT and the Northern Territory), and a unit root in the other four. Our results from Section 4 on the stationarity of relative unemployment rates are also mixed, with some state unemployment rates found to be cointegrated with the national rate while others are not. The relative participation rate is generally found to be stationary.

Based on the panel unit root results we tentatively conclude that the employment share is integrated of order 1 and the relative unemployment rate and the relative participation rate are stationary. The model specification we use is:

where j denotes a state.

This system can be viewed as the reduced form of an (unknown) structural model of regional labour markets. The structure described above is a standard VAR except that changes in the share of total employment (Δem) feed through simultaneously into the unemployment rate and the participation rate (ur and pr).

Since we model the relative unemployment rate as a stationary variable, our specification dictates that, at least in the long run, shocks to state unemployment rates relative to the national rate will be eventually unwound. Therefore our assumptions imply that migration does work in the long run to eliminate unemployment differentials between states. There may, however, be persistent differences between state unemployment rates during the adjustment process to a shock. As the figures in Section 4 and the unit root tests suggest, this process of adjustment might take many years in some cases.

Given data limitations we impose the rather strong assumption that the responses to a shock (that is the coefficients) are identical across all states. This assumption is unlikely to hold true in practice. Our results should thus be interpreted as the average response across states to a labour demand shock. The model does incorporate fixed differences between states by allowing the constant term α to vary across states. Thus, the model can allow for constant steady-state differences in unemployment rates or participation rates between states but the adjustment path to a shock is the same in each case. For the moment, the effect of a labour demand shock on the real wage is ignored; this transmission channel is introduced in Section 5.2.

5.1 Estimation Results

The model is estimated using ordinary least squares^[10] over the period 1979:Q2 to 1997:Q1, which with six states and two territories yields a total of 576 quarterly observations.^[11] A common lag length of six quarters is employed for each equation.^[12] Tests of the joint significance of the lags of each variable in each of the three equations are presented in Appendix B. Each of the variables is significant in each equation at the 1 per cent level. The adjusted R² for the unemployment rate and participation rate equations are high, 0.87 and 0.99 respectively. The adjusted R² for the employment equation is much lower (0.25), in part reflecting the fact that the employment variable is modelled in first differences.

Figure 6 summarises the results by showing the response of the system to a 1 per cent negative shock to the employment equation. The upper panel shows the impulse response of employment, unemployment, and the participation rate to the employment shock. The unemployment rate and participation rate shown are the actual percentage point deviation of each variable from the baseline.^[13] Initially, the 1 per cent decrease in employment results in a decrease in the participation rate of 0.4 per cent, and a 0.2 per cent increase in the unemployment rate. Most of the initial decrease in employment is later reversed. The participation rate and unemployment rate return back to their base levels (by construction). The process of adjustment takes approximately four years.

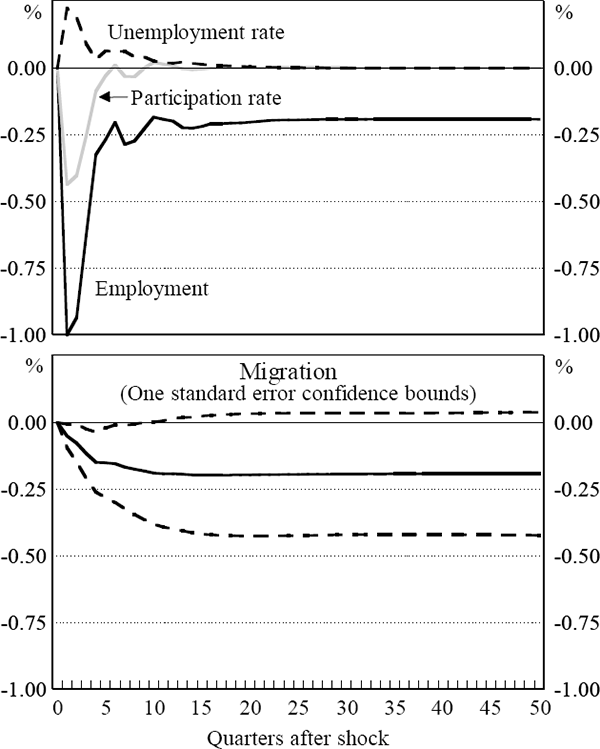
The lower panel shows the net migration response to the negative employment shock, which is computed as a ‘residual’ from the time path of the three variables in the VAR.^[14] Approximately half of the out-migration occurs in the first year after the shock, and three quarters of the net migration is complete within two years of the shock. The cumulative out-migration generated increases steadily, reaching its peak three years after the shock.

Figure 6 also presents one standard error confidence bounds for net migration. These were obtained through stochastic simulation with 1,000 replications. Notably, zero is (just) inside the confidence band for the migration response. Thus, although our point estimate of the level of net migration in the long run is negative (−0.19), a considerable degree of uncertainty should be attached to this figure. Confidence bands were also generated for each of the three variables in the model, although for clarity, these are not presented in Figure 6. The bands are of similar width to the confidence intervals reported in Blanchard and Katz (1992). The largest uncertainty is associated with the employment response.

5.2 Incorporating Wages

The above analysis ignores the potential effect of lower labour demand in a state on the real wages in the state. As discussed in Section 2, the net effect of the real wage on migration is ambiguous. A lower real wage can increase labour demand, reducing unemployment and thereby decreasing mobility; but a lower real wage also increases the incentive to move interstate to seek higher-paid employment. Consequently we extend the VAR framework to include real wages.

The wages variable is defined as follows:

Wage measures the relative level of average weekly earnings, compared to the national average. Individual unit root tests conducted on the wage variable were inconclusive, with five of the eight states indicating a stationary relative wage. The panel unit root test suggested that wage was I(1) at the 5 per cent level of significance (although not at the 10 per cent level). Based on these somewhat inconclusive results, wage is initially modelled as an I(1) variable, allowing the impulse response of relative wages to deviate from zero in both the short and long run. We investigate the effect of modelling wage as I(0) in Appendix B.

Real wage data is available by state only from 1981:Q4. Furthermore, wages data from the ACT and Northern Territory is not available until even later (1983:Q4), and is of relatively poor quality. As a result, the model was estimated from 1981:Q4, with the two territories excluded from the analysis. The three-variable model described at the beginning of this section is appended by including the first difference of the wage variable described above. Summary statistics for this model are presented in Appendix B.

In the first three equations, each of the four variables is usually significant in explaining variation in the dependent variable. The exception is the wages equation, where the level of the other three variables (i.e. the relative labour market conditions in the state), play little role in determining the increase in real wages. In addition, the adjusted R² for the wages equation was only 0.09. These results suggest that state wage bargaining processes in Australia over the sample period were largely driven by factors other than relative labour market conditions. This in turn implies that wage adjustments provide only a weak mechanism for the transmission of labour demand shocks.

Impulse response results from this four-variable VAR are presented in Figure 7. In this specification, a 1 per cent negative shock to employment is associated with a rise in the unemployment rate of approximately 0.3 per cent. The participation rate decreases initially by 0.4 per cent before rising back towards its baseline value. The looser labour market conditions also place some slight downward pressure on wages. The effect on wages occurs with a lag: the decrease in relative wages peaks near 0.3 per cent, one year after the shock. In the long run, the participation rate and unemployment rate return to their baseline values, while there is a permanent downward shift in the real wage. Again, this permanent difference is a direct result of modelling the real wage in differences.

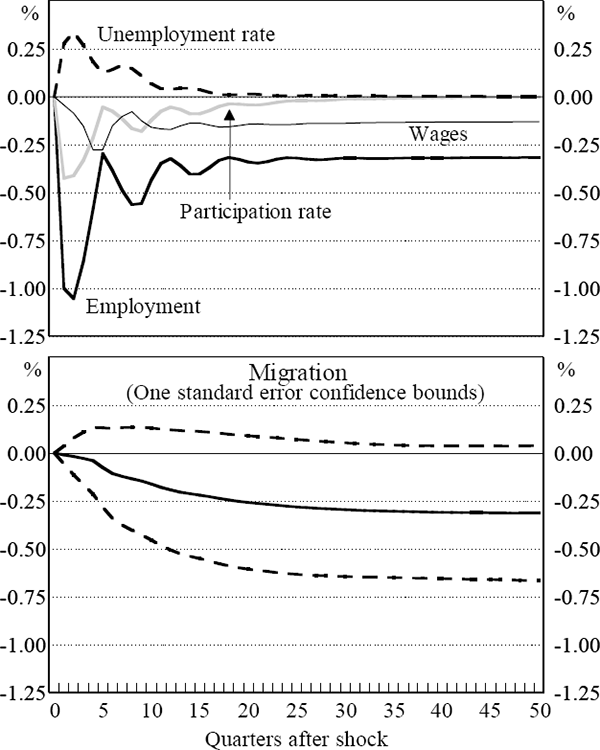
The 1 per cent negative shock to employment causes long-run out-migration of 0.31 per cent of the labour force. This out-migration occurs gradually over a number of years. There is a small amount of net out-migration in the first year after the shock. Approximately one third of the out-migration takes place within two years, and nearly two thirds of the net migration takes place within three years of the shock. The rate of out-migration then flattens out, although it is seven years after the initial shock before the out-migration is entirely complete. The slow initial migration response and the long period over which migration occurs appears reasonable, given the inertia associated with a decision to move interstate, and the high costs of adjustment involved.

The magnitude of the impulse responses for the four-variable model is broadly consistent with the responses in the three-variable model presented in Figure 6. The process of migration does, however, occur over a longer period than in the three-variable model. It should be noted that the results are not exactly comparable with those above, because the sample periods are different, and the four-variable VAR excludes the Northern Territory and ACT.

The speed of adjustment is broadly consistent with results found by Blanchard and Katz (1992) for the United States, and Decressin and Fatas (1995) for Europe. However, the dynamics of adjustment are quite different in each case. In Blanchard and Katz, employment continues to fall further after the initial shock, and significantly overshoots its long-run response value. After one year the fall in employment is double the initial shock, before finally converging to a long-run response of 1.3 times the initial size of the shock. The impulse response of employment for Europe is closer to the results presented here; in Decressin and Fatas, the employment response falls away towards zero in the periods following the shock.

Explaining the difference in the dynamics between the US and Australia is a difficult task. The Blanchard and Katz results for the US are consistent with Diamond-type externalities. For example, if the employment shock is the closing of a particular industry, one might expect spillovers into other industries that supplied the industry, so that the long-run effect exceeds the short-run effect. In contrast, our results suggest that Australian states have an internal adjustment process that mitigates the size of the initial shock. For example, a boom in mining may generate a surge in construction employment which dies out over time so that the long-run boost to employment is less than the initial increase.

Another possible explanation for our result is that, after a positive demand shock, the increase in the real wage tends to dampen the initial employment shock, so that there is some drop-off in employment creation. Conversely, the fall in real wages following a fall in labour demand may induce firms to move into a depressed region lessening the impact of the initial adverse shock. Thus the Australian results could possibly reflect a higher degree of firm mobility.

However, wages are generally regarded as being more flexible in the US than in Australia, so one would expect that the off-setting effect of the wage response to the initial employment shock would be greater in the US than in Australia. Rather, Blanchard and Katz find a large multiplier effect, in spite of the movement in wages. This result then remains something of a puzzle.

To gauge the incremental effect of the wage channel on migration, we recalculate the impulse responses while setting the wage response equal to zero. From this, we can see how suppressing the wage channel affects migration and other impulse responses. Suppressing the wage channel resulted in out-migration of 0.29 per cent after 50 quarters (almost identical to the estimate of 0.31 per cent above).

Extending the model to include the real-wage channel acts to marginally increase the migration response to the decreased labour demand. However, the impulse responses of the unemployment and participation rates, and the migration response, are little altered by the suppression of the real wage variable. Furthermore, the migration response when wages are suppressed is well inside the one standard error confidence band of the four-variable model.

Taken together, the results presented above suggest the introduction of a wages channel does little to change the employment and migration dynamics. This is possibly, in part, related to the federally based award system that existed over much of the sample period. This finding is also consistent with the implication of the Harris-Todaro model that risk-averse workers should care more about relative employment opportunities than about the wage in assessing their migration decision. Blanchard and Katz also find that the addition of a wage variable to their model makes little difference to their results.

As mentioned earlier, the Industry Commission (1993) investigated labour mobility in a framework very similar to that employed here. However, that study adopted different stationarity assumptions for the variables in the system so that the system was estimated as a vector error correction model. These different assumptions appear to be the major explanation for the conclusion of that study that migration plays very little role in labour market adjustment. In contrast to the findings of this paper, the Industry Commission concludes that the participation rate is the main adjustment mechanism. Labour mobility plays a much weaker role than in our model and is close to zero, three quarters after a shock.

We conducted a range of exercises to test the sensitivity of our results to changes in model specification. A detailed discussion of this sensitivity analysis is provided in Appendix B. We find weak evidence that the size of the migration response to a shock is larger in the second half of the sample, although the size of the difference is not statistically significant, and the speed of adjustment is similar. Changing the order of integration of the variables in the VAR usually acts to reduce the size of the migration response, however, a negative shock to labour demand still induces out-migration in nearly all cases. We find that if annual data instead of quarterly data is used to estimate the model (annual data was used in Blanchard and Katz's study), the speed of adjustment to a shock is somewhat slower. Finally, the model conclusions are robust to the exclusion of each individual state in turn.

5.3 State Fixed Effects

In the model described above, permanent differences between states are modelled by allowing the constant term to vary between states for the same equation. In this way, the model can incorporate permanent differences between participation rates, unemployment rates, employment growth rates or growth rates in relative wages in different states.

We test whether these permanent differences between states are significant in a statistical sense. If the state fixed effects are significant, then unemployment rates will not converge to one uniform national rate, even in the long run. Instead, there will be a different steady-state unemployment rate in each state and territory.

F-tests are conducted to test the joint significance of the state fixed effects for each of the four equations in the model.^[15] For each equation except the wages equation, the state fixed effects are found to be jointly significant at the 1 per cent level of significance. This suggests that there are deterministic differences in labour force patterns between states. As further evidence of the importance of permanent differences between states, the four-variable model re-estimated without state fixed effects is found to be dynamically unstable, suggesting that the exclusion of state fixed effects represents a fundamental mis-specification of the appropriate model structure. That the restriction is valid in the wages-growth equation again possibly reflecting the nationally based wage structure embedded in the Australian wage-fixing system over the sample period.^[16]

In our modelling work, we assume that the fixed effects for each state are independent of the shocks to employment. An implication of this is that (for instance) the relatively high rate of unemployment in Tasmania reflects a preference for Tasmanian residents to live in that state, rather than the outcome of a sequence of adverse shocks to unemployment in Tasmania. If this assumption of independence is invalid then state specific shocks may permanently influence relative state unemployment rates.

Alternatively, it may be the case that the high unemployment rates in Tasmania and South Australia reflect a series of negative shocks to employment whose effect on unemployment, while temporary, has not yet dissipated. In this case, the unemployment rates of Tasmania and South Australia might be expected to eventually return to the national rate after a period of continuing net out-migration.

Footnotes

The distinction between defining this variable in terms of employment rates or unemployment rates is not crucial, since ln[(1 − U_S) /(1 − U_N)] ≈ U_N − U_S, whereas ln(U_S/U_N) = ln(U_S) − ln(U_N). [9]

An alternative estimation technique would be to apply Feasible Generalised Least Squares (FGLS), which is asymptotically efficient where there are correlations between the error terms in each equation in the system. In the context of a standard VAR, it can be shown that OLS is equivalent to FGLS because the same set of right-hand-side variables appears in every equation. This is not strictly true of the system estimated above, because Δem enters contemporaneously into two of the equations. But it was found through some preliminary estimation that the gains to using FGLS are small in this context, because of the near-VAR structure of the model. [10]

The data is available at a monthly frequency, but is aggregated into quarterly observations for estimation purposes. The primary motive for this is so that wages (which are only available on a quarterly basis) can be added seamlessly to the model. Estimation results are generally robust to whether quarterly or monthly data is used. [11]

The Schwarz criterion indicated an optimal lag length of 1, which would not provide a rich enough dynamic structure for the model. Consequently, six was chosen as a ‘reasonable’ lag length. As is demonstrated in the sensitivity analysis in Appendix B, the choice of a lag length is not crucial to the inferences generated from the VAR model. [12]

These are derived from the ur and pr variables using d(U/L) = (E/L)*dln(L/E) and d(L/P) = L/P*dln(L/P) where E, L and P refer to employment, the labour force and population respectively. [13]

It can be obtained from the identity: dln(P) = dln(E) − dln(E/L) − dln(L/P), where P is population, L is the labour force and E is employment, and all variables are expressed as a proportion of the national level. [14]

The form of the F-test used here can be found in Greene (1993, p. 468). [15]

These results are consistent with the finding of Groenewold (1992) that long-run equilibrium differences in unemployment rates exist between states. Groenewold also finds that equilibrium wage levels differ between states. This is a different hypothesis to testing the significance of constant terms in our wage equation. We are testing for equality of wage growth rates between states (since our wage variable is modelled in log-differences). [16]