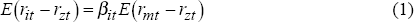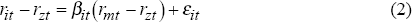RDP 9802: Systematic Risk Characteristics of Corporate Equity 2. Is Systematic Risk Convergence a Statistical Artefact?

To date, attention has focused on the behaviour of a particular estimator of systematic risk, popularised in the late 1960s and early 1970s by empirical studies of the Capital Asset-pricing Model (CAPM). Before describing the early evidence of systematic risk manipulation, it is necessary to discuss how the CAPM as developed by Treynor (1961), Sharpe (1964), Lintner (1969), Mossin (1969), and Black (1972) is fundamentally related to measures of systematic risk.

The CAPM is a single-period model of asset returns, based on the mean-variance optimisation of Markowitz (1959) and the equilibrium assumption that markets clear. Mean-variance analysis delivers two-fund separation such that the expected return on any minimum-variance portfolio can be expressed as a linear combination of the expected returns on any two other distinct minimum-variance portfolios. In the zero-beta CAPM of Lintner and Black, the two minimum-variance portfolios of interest are the market portfolio and the zero-beta portfolio (the portfolio with zero correlation with the market portfolio). Alternatively, in the standard CAPM, the two minimum-variance portfolios of interest are the market portfolio and the risk free security. The market clearing condition implies that the return on the market portfolio is efficient in the sense that it is the portfolio with the minimum variance, given its expected return.

The CAPM defines a useful empirical measure of an asset's systematic risk. This measure of systematic risk is the coefficient, β_i, on the market portfolio's expected return in the equation defining the equilibrium relationship between excess returns on the firm and excess returns on the market:

where r_it is the return on asset i, r_zt is the return on the risk free or zero-beta portfolio and r_mt is the return on the market portfolio.

To estimate the relationship between returns (with its CAPM interpretation), several substantial steps must be taken. First, Equation (1) must be converted from its ex ante form by replacing the expected returns with observed data. This conversion implicitly assumes that the rate of return on any asset is a ‘fair game’ so that, over many realisations, the expected return will equal the average return. In other words, expectations are not biased. With normally distributed returns and independent expectation errors, this fair game assumption delivers an ex post equation:

It is also necessary to identify and measure the return on the market portfolio so that it can be used as a regressor on the left-hand side of Equation (2). In this regard, r_mt is often approximated by an average return on the entire equity market. Then, in a population regression, β_it is estimated by:

where 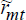is the proxy for r_mt. Clearly 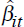is a positive linear transformation of the covariance between firm i's return and the proxy for the market return. In this way it can be interpreted as a measure of systematic risk.

As Roll (1977) points out, the market portfolio includes all possible assets. Specifically, it is not sufficient to use an average of returns within the equity market alone. Roll shows that the only valid way to test the CAPM is to test whether the true market portfolio is mean-variance efficient. Because the true market portfolio is impossible to construct, Roll concludes that standard CAPM testing strategies, using proxies for the market portfolio, are uninformative.

However, this caveat on the literature testing the CAPM does not interfere with the usage of estimated betas in Equation (2) as measures of systematic risk. Interpreting the betas in Equation (2) as measures of systematic risk does not depend on a market-clearing condition or mean-variance efficiency of the approximation for the market return. Thus, approximating the market portfolio with the value-weighted average return on the equity market does not interfere with the interpretation of the betas, estimated from dynamic versions of Equation (2), as measures of market-wide or systematic risk.

Given that the CAPM yields a useful measure of systematic risk, one would expect variations in systematic risk to be evident in studies that attempt to estimate Equation (2). During the period of intensive testing of the CAPM in the 1970s and early 1980s it was widely observed that estimated equity betas evolve through time to eventually exhibit systematic risk characteristics that are similar to those of the entire equity market.^[1] More precisely, in sequential sub-samples, estimates of beta tend towards unity.^[2] Black, Jensen and Scholes (1972), Blume and Friend (1973), and Fama and MacBeth (1973) refer to this phenomenon as beta convergence. These studies all test the CAPM in two stages because of a suggestion by Blume (1970) that measurement error in estimates of equity betas for individual securities is ameliorated to some extent by using the equity returns on portfolios formed from groups of firms in the sample. First, equity betas are estimated for all stocks individually. The stocks are ranked by these initial beta estimates and grouped into a number of portfolios. The ranking process is intended to retain variation in equity betas across portfolios of firms.

In the second stage, a subsequent sample period is used to compute betas for each portfolio. These portfolio betas are then used in cross-section regressions explaining excess rates of return using equity betas and a number of additional explanatory variables that should not be significant under the assumptions of the CAPM model. Typically, these and other studies have found that there is a consistent tendency for the second-stage beta estimates to be less extreme than the first-stage beta estimates. The first stage beta estimates of portfolios can be shown to be the average of the first stage betas estimates of the firms comprising the portfolio.

The most popular explanation for this convergence phenomenon is that it is driven by measurement error. This explanation has Bayesian foundations. Fama and MacBeth (1973, p. 615) explain that forming portfolios of securities that have been ranked by their estimated betas ‘causes bunching of positive and negative sampling errors within portfolios’. 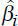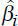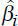The intuition is that, again from Fama and MacBeth, ‘in a cross section of , high tend to be above the corresponding true β_i and low observed tend to be below the true β_i’. A firm is grouped into a low beta portfolio either because it had a low beta or because its beta estimate had a negative measurement error. Thus negative measurement errors are bunched in the low beta portfolios. Similarly, the positive measurement errors tend to be bunched in the high beta portfolios. When new betas are estimated for the portfolios in subsequent time spans, the measurement errors within each portfolio have zero expected value and so a convergence of extreme portfolios towards the market beta should be observed.

However, other authors have discovered a similar convergence phenomenon when estimating the equity betas of individual firms rather than portfolios. Klemosky and Martin (1975) show that naive, no-change forecasts of a firm's beta often have twice the mean-square forecasting error of methodologies that explicitly adjust OLS beta estimates towards the market beta. This paper and other studies focus on the betas of individual firms suggesting that portfolio formation is not the only reason for the convergence witnessed in CAPM tests. This finding has provoked a more focused study of the convergence phenomenon. Is beta convergence a statistical artefact or a behavioural phenomenon?

The statistical artefact argument has been made rigorous in Blume (1975) and Vasicek (1973) using the Bayesian concept of prior distributions. Both argue that in the cross section we tend to observe equity betas that are normally distributed around unity and concentrated between zero and two. Using this prior information to form a Baysian estimator of equity betas should eliminate the measurement error bias because it is a weighted average of the classical estimator and the prior expected value of the equity beta.^[3] The weight placed on the classical estimator depends on the information content in the data sample. With such short data samples being used to estimate equity betas in tests of the CAPM, the sample likelihood function does not dominate the prior information and so the prior information will adjust estimates of equity betas toward unity. This adjustment should eliminate the measurement errors that have affected previous tests of the CAPM.

Using portfolios of equity securities, Blume (1975, p. 785) tests whether the beta convergence observed in the CAPM tests can be entirely explained by the omission of prior information and finds that the convergence tendency of adjusted estimates of equity betas remains significant at the five per cent level. The test is of the null hypothesis that a cross-section regression of adjusted betas in period one on actual betas in period two yields a slope coefficient equal to zero. Blume concludes that ‘a major reason for the observed regression [to unity] is real non-stationarities in the underlying values of beta and that so-called ‘order bias’ is not of dominant importance’.^[4]

Although this paper reaches similar conclusions, it does so using a substantially different methodology. Beta estimates are obtained for individual firms rather than for portfolios preventing measurement errors from being aggregated as in previous studies. While betas for individual firms have large standard errors compared to the betas of portfolios, this should not cause convergence. This paper is also differentiated from previous work by the fact that the estimation of sequential betas is done using the Kalman Filter which optimally updates the next beta based on the current beta and the next observation on equity returns.

This approach, of formally modelling the variation in equity betas avoids the contradiction, inherent in previous studies, of estimating betas under the assumption that they are fixed in sample and then making inferences about their movements through time. Obtaining a time series of equity betas for individual firms facilitates characterisation of the law of motion governing the adjustments from the current beta to the beta in the next period. It is the features of this law of motion, rather than the types of tests conducted by Blume that form the basis of the conclusion that equity betas tend to converge toward unity.

Despite these substantial differences, Blume's Bayesian approach to incorporating prior information is retained by applying a tight prior to the initial estimate of each firm's equity beta. The initial beta estimate is then updated using the Kalman filter so that the prior information gets carried through to estimates of beta throughout the entire time dimension for each firm. This use of prior information prevents measurement error from being related to the extremeness of beta estimates.

This paper also goes beyond the previous studies of equity beta convergence by characterising the relationships between the distribution of equity betas across firms and observed characteristics of firms. The measurement error view of beta convergence cannot explain the increased probability of delisting for firms with extreme betas or the relationship between the concentration of betas and the size and age of firms. By demonstrating that such relationships are a robust feature of the data, the view that beta convergence is a statistical artefact is more strongly refuted.

Remaining is the alternative hypothesis that beta convergence is behavioural. This theory is strongly supported by Blume (1975) who finds that the order bias arising from measurement error in the context of portfolios of securities explains less than half of the observed convergence in equity betas. He concludes that firms with extreme betas seem to take on investment projects with less extreme risk characteristics. This conclusion ignores the many channels through which firms may adjust the risk characteristics of their equity returns by manipulation of their financial structures. Equity issues, leveraged buy-outs and equity carve-outs are examples of such manipulations that will influence the systematic risk profile of the income stream generated by equity holdings. Nonetheless, the essential point that beta convergence is not merely a statistical artefact remains clear. The next two sections investigate Blume's results in a more sophisticated manner, avoiding the many difficulties plaguing beta estimation using portfolios of securities.

Footnotes

Contributors to this literature include Friend and Blume (1970), Black, Jensen and Scholes (1972), Miller and Scholes (1972), Blume and Friend (1973), Blume and Husic (1973), Fama and MacBeth (1973), Basu (1977), Reinganum (1981), Litzenberger and Ramaswamy (1979), Banz (1981), Gibbons (1982), Stambaugh (1982) and Shanken (1985). [1]

The beta for the market return is unity by definition. [2]

The weighted average property of the Baysian estimator requires the loss function to be quadratic. [3]

Order bias is that bias in systematic risk estimates arising from measurement error. [4]