RDP 9812: An Optimising Model for Monetary Policy Analysis: Can Habit Formation Help? 5. Monetary Policy Implications of the Model
September 1998
- Download the Paper 395KB
An alternative interpretation of the results of this paper and Fuhrer (1997a) is that the restrictions imposed on the price specification and the funds rate reaction function are invalid, and are interfering with the real-side dynamics of consumption and output. To test this possibility, I estimate a model with reduced-form processes for consumption and income, so that only the restrictions from the price and interest rate specifications constrain the model. This model allows us to isolate the effects of these restrictions.[8]
A comparison of the autocovariance function for this model (Figure 4) with the unconstrained autocovariance function suggests that this interpretation is invalid. The Fuhrer–Moore price specification and the simple reaction function capture the dynamics in these variables without distorting their dynamic interactions with consumption and income (or vice versa).
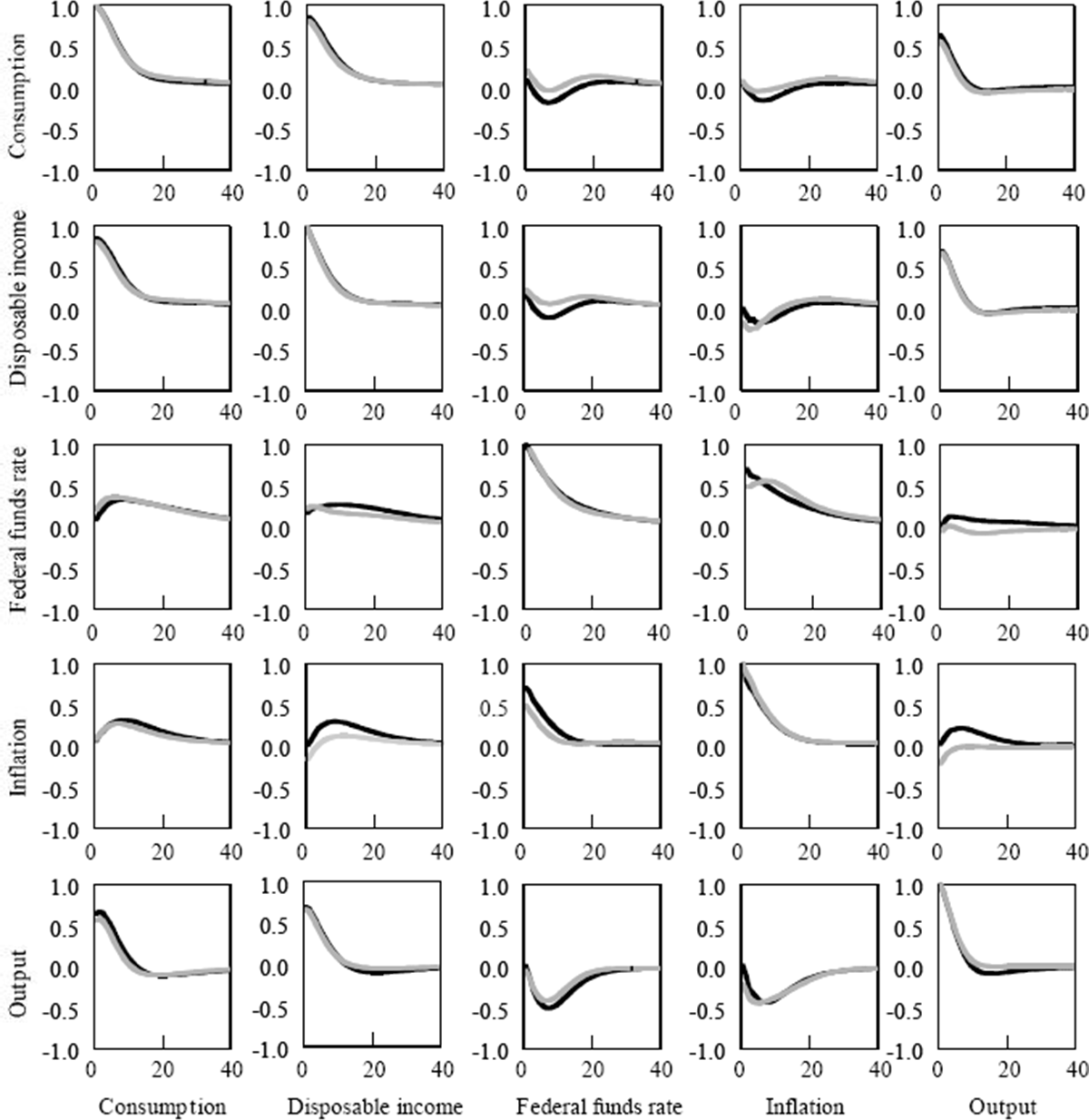
Notes: Ordinate: lags in quarters. Co-ordinate: correlation function. Black lines, unrestricted; grey lines, restricted.
It is the case, however, that improper specification of the real side of the model can distort the dynamics of inflation and nominal interest rates. This should not come as a surprise, given the structural links between real output and inflation in almost any price specification, and given the assumed response of nominal interest rates to real output in the policy reaction function. Figure 5 below provides an example of such a case.
5.1 Disinflation in the Models
In Fuhrer (1997a), a disinflation simulation highlighted the ‘front loaded’ responses of real variables to a monetary shock. This information is, of course, contained in the vector autocovariance function, but the simple disinflation simulation makes a key problem of the specification quite clear. Note that the specification including rule-of-thumb consumers still exhibited rapid response to shocks; we wish to determine whether the addition of habit formation improves this counterfactual behaviour in the model.
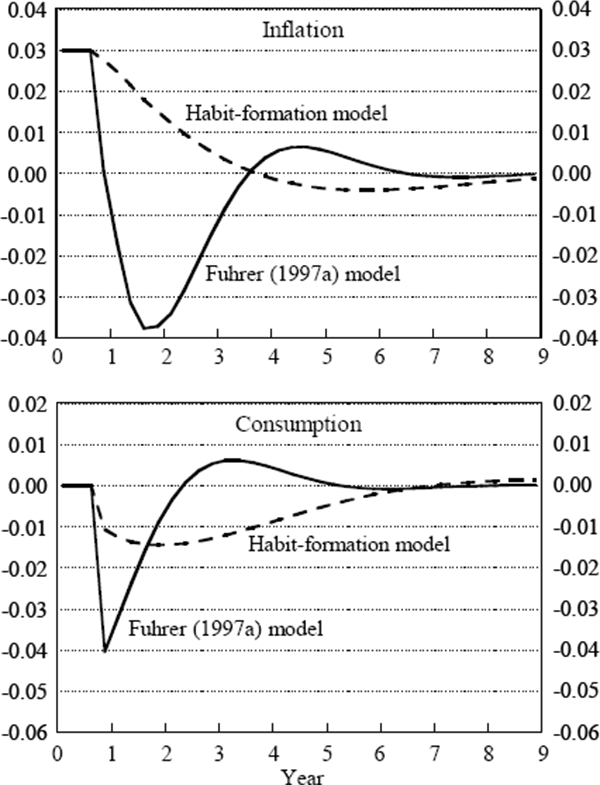
The simulation is straightforward. Starting from a steady state, I decrease the long-run inflation target from about 3 per cent to 0 per cent. The decrease is unanticipated. It is informative to compare the response of the model without habit formation to the model that includes it. Figure 5 displays the results of the simulation.
In the model with habit formation, inflation falls gradually from its old steady state to the new, lower equilibrium. Interestingly, consumption also responds gradually, with its peak response at a year or so; the full response takes three to four years. This response contrasts markedly with that of the model excluding habit formation (from Figure 4 in Fuhrer (1997a)), shown in the solid lines in the figure. Note that the solid lines exhibit an example of a model in which the mis-specification of the real side compromises the behaviour of the nominal side. The persistence of inflation in this model, as indicated in the solid line in the top panel of Figure 5, is significantly decreased by the rapid (and counterfactual) response of real variables to a disinflationary shock.
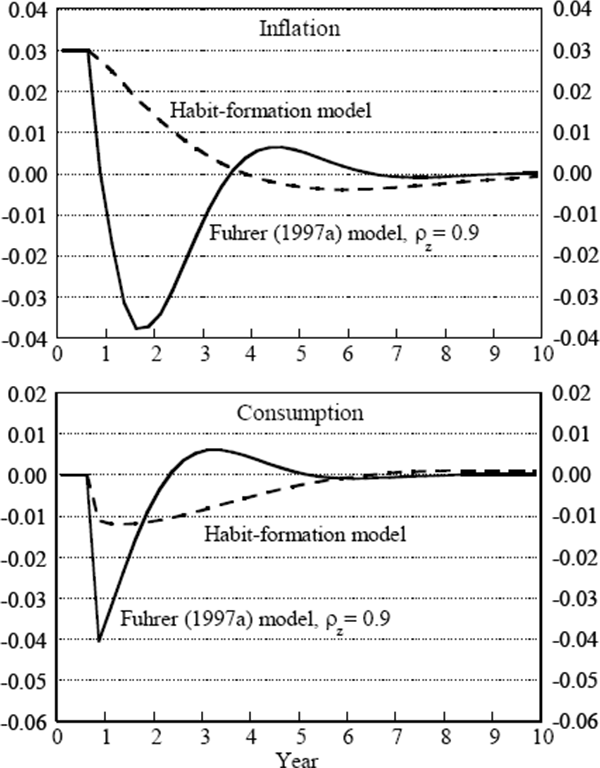
Figure 6 assesses the impact of the length of ‘memory’ in the habit reference level on the model's dynamics. In this figure, I perform the same disinflation simulation, substituting a value of 0.9 for ρz (recall that the estimated value is 0.001). As a comparison of Figures 5 and 6 shows, the model's behaviour is altered only slightly by the change from one-quarter memory to more persistent memory in the reference level.
Footnote
The converse of this test is performed above: The model with restrictions on consumption, but without restrictions on prices and interest rates, requires rule-of-thumb and habit formation behaviour to match the moments in the data. [8]