RDP 1999-08: Inflation Targeting and Output Stabilisation 4. Evidence
June 1999
- Download the Paper 135KB
The model presented in Section 2 has provided the basis for a growing body of empirical work examining the trade-off between output and inflation variability.[6] The general approach that has been adopted in this literature has been to stochastically simulate a version of the model. The weight on output stabilisation (λ) is varied, and a variability frontier is then traced out for an optimal monetary policy response and for various policy rules. This section summarises the findings of the literature, focusing particularly on the results that have been obtained for Australia.
Stevens and Debelle (1995) estimate the model in Section 2 using Australian data, taking into account a slightly more complicated lag structure. The policy-maker is assumed to have complete knowledge of the structure of the economy, but is assumed to respond to shocks with a one-period lag. If policy is conducted optimally, the trade-off frontier in Figure 1 is obtained.
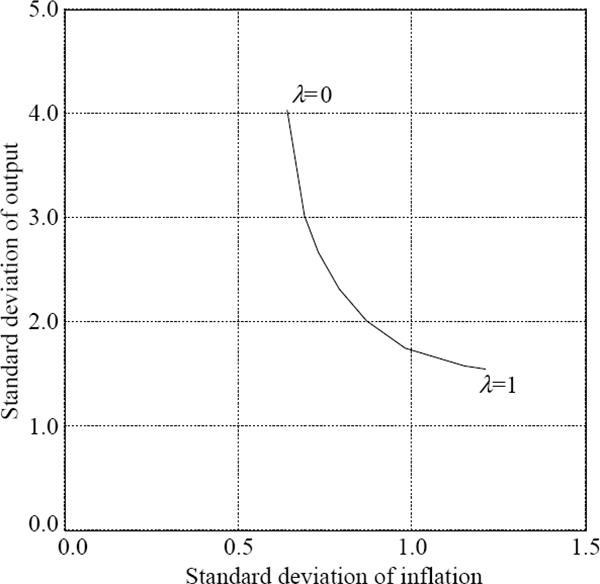
As Figure 1 shows, the trade-off between inflation and output variability is convex: increasing the weight on output in the central bank's objective function (moving south-east on the curve), increases the variability of inflation while reducing the variability of output relatively substantially in the upper-left portion of the curve, but less so in the lower-right portion.
There are two other noteworthy features of the curve. Firstly, when there is no weight on output stabilisation (λ=0), there is little cost in terms of increased inflation variability from small increases in the weight on output stabilisation, but this significantly decreases the variability of output. Secondly, a large range of values of λ deliver very similar outcomes for inflation and output variability. These are clustered around the part of the trade-off curve closest to the origin. Major differences occur only when very large weights are put on either inflation or output stabilisation. These conclusions have been found for a range of countries.[7]
In deciding upon the appropriate weight to put on output stabilisation in the objective function, the following consideration should be borne in mind. The initial choice on the variability frontier may influence the speed with which the central bank acquires credibility, and hence, the choices available to it in the longer term (that is, the long-run position of the trade-off curve). A point such as A in Figure 2 which aimed for lower inflation variability may enable a central bank to establish its inflation-fighting credentials earlier than one which aimed for lower output variability. As its credibility became established, the central bank might then be able to follow a more flexible approach (point B), potentially on a variability frontier closer to the origin.
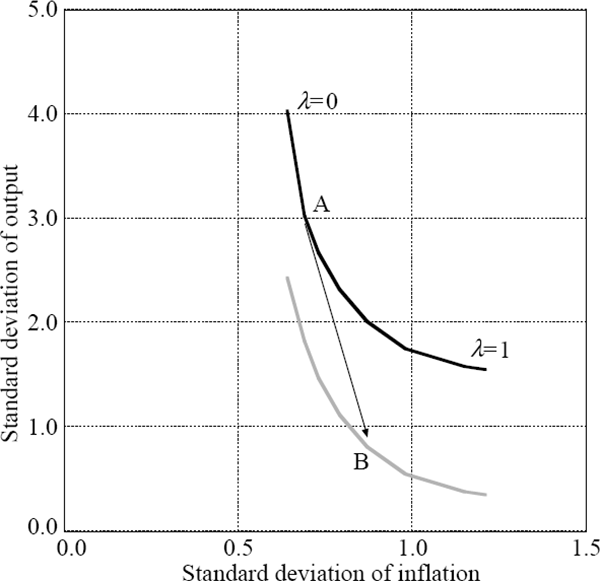
The above results can be used to consider the issue of the appropriate width of the inflation-target band. The curve in Figure 1 was obtained under the assumption of optimal policy where the central bank has full knowledge of the economy's structure. However, even when the central bank puts zero weight on output stabilisation, the standard deviation of inflation is still 0.64 per cent per quarter. Thus a band wide enough to ensure that it was breached only a small fraction of the time would likely be too large to be credible.[8] There are some caveats to this conclusion. Most notably, if over time, the inflation target became more credible, the structure of the economy and in particular, the inflation equation would change, lowering the irreducible variance in inflation (this issue is revisited in Section 5).
de Brouwer and O'Regan (1997) extend the above analysis using a more fully specified model of the Australian economy that explicitly incorporates the exchange rate. They evaluate the performance of different monetary policy rules in terms of their effect on inflation and output variability. The rules they consider include:
|
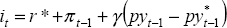 ; ;
|
|
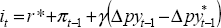 ; ;
|
|
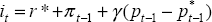 ; ;
|
|
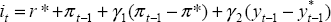 ; ;
|
|
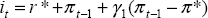 ; and ; and
|
|
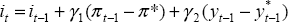 . .
|
Again, stochastic simulation of a small model of the Australian economy under each of these different rules yields the output/inflation variability trade-off curves in Figure 3.[9]
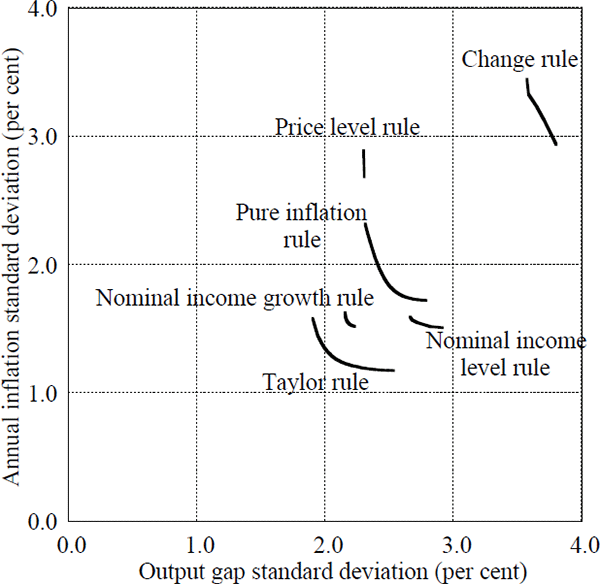
Figure 3 shows that a Taylor rule outperforms other monetary policy rules in terms of reducing both inflation and output variability. Notably, a Taylor rule outperforms the ‘pure inflation’ rule which focuses only on inflation. Not only does it result in lower output variability but it also lowers the overall variability of inflation. This is because the output gap is a major determinant of inflation, but the inflation-only rule does not pay sufficient attention to output.
It should be noted that the ‘pure inflation’ rule does not correspond to strict inflation targeting. As shown in the model in Svensson (1997b) and Ball (1997), even under strict inflation targeting, the central bank's reaction function places a positive weight on output. The difference between strict inflation targeting and flexible inflation targeting is reflected primarily in the weight placed on output in the reaction function. The empirical literature demonstrates the choice set or efficient frontier available to policy-makers from conducting optimal policy, or from following a particular type of policy rule. The policy-maker's preferences embodied in the objective function determine the choice of the point on the frontier.
The Taylor rule also outperforms a nominal-income targeting rule. This result may be particular to the framework employed by the authors. For example, Bryant, Hooper and Mann (1993a) find that the two rules deliver approximately equivalent outcomes. The key issue here is the degree to which agents are forward-looking.
The framework that de Brouwer and O'Regan employ uses adaptive expectations whereas Bryant et al uses rational expectations. Adaptive expectations result in greater persistence in the inflation process which tends to improve the relative performance of the Taylor rule.[10]
It is important to keep in mind that a Taylor rule is not the optimal policy rule in any but an extremely simple model of the economy. Hence, de Brouwer and O'Regan also examine how the trade-off can be improved (that is, shifted towards the origin) beyond that delivered by the adherence to a simple Taylor rule.
Firstly, the output/inflation variability trade-off is improved the more credible is the policy framework. In particular, the inflation target can serve an important role as an anchor for price and wage setters. The greater the credibility of the target, the less that inflation expectations will adjust to shocks to inflation, decreasing the need for policy to offset the impact of those shocks. Consequently, the inflation process will have more inertia around the stable mean of the inflation target. Measures to increase public understanding of the inflation target, including through a sufficient degree of transparency in the central bank's conduct of policy, can be beneficial in this regard.
In this respect, an inflation target has an advantage over a nominal income target. The nominal income target does not provide an explicit decomposition into an inflation component and an output component, so there is no obvious anchor for inflation expectations. Furthermore, the inflation rate is generally well understood by the public whereas nominal income growth may be a more opaque concept.
Secondly, the Taylor rule in its standard form is a backward-looking rule. However, monetary policy in an inflation-targeting regime (and indeed in most policy frameworks) is forward-looking, given the lags in the effect of monetary policy on the real economy and inflation. Friedman (1959) and Blinder (1997) have highlighted the perils of a policy rule which fails to take account of the policy lags. Consequently, a rule which incorporates forward-looking variables can deliver superior outcomes. There are two alternatives in this regard.
A rule which incorporates other variables that affect the future path of output and inflation will improve the trade-off. For example, de Brouwer and O'Regan show that including the exchange rate and unit labour costs in the central bank's policy rule can reduce the variability of both output and inflation.
Alternatively, the policy rule can explicitly include forecast values of output and inflation. That is, the policy rule itself is forward-looking. Again, such a rule reduces the variability of both inflation and output. This occurs because the policy rule now takes direct account of the policy lags.
Batini and Haldane (1999) examine this last issue for the UK economy. They evaluate the performance of an inflation-forecast targeting rule. They show that such a rule is ‘more efficient at minimising inflation and output variability than standard Taylor rule specifications, and [is] almost as efficient as fully optimal rules’ (p. 5). In addition, an inflation-forecast targeting rule has a number of other desirable properties. Its simplicity implies that it is more robust than other policy rules to uncertainty about the structure of the economy and it is more easily monitored than other rules.
The other important issue that Batini and Haldane highlight is that the degree to which policy-makers care about output (the size of λ) affects the horizon of the inflation forecast. They confirm the theoretical result established by Ball (1997) and Svensson (1997b) that the greater the weight on output, the more gradually the policy-maker responds to deviations of the inflation forecast from the target value. In practical terms, this corresponds to a longer horizon on the inflation forecast in the policy rule.
In conclusion, the empirical literature has generally supported the conclusions of the theoretical literature. Namely, sizeable gains can be achieved in terms of output stability at the cost of only a small increase in inflation variability when a more flexible approach to inflation targeting is pursued. Secondly, because output is a major determinant of future inflation, placing a positive weight on output stabilisation in the central bank's reaction function will always improve inflation outcomes over a reaction function which responds only to inflation, regardless of whether a strict or a flexible inflation-targeting regime is being pursued.
Footnotes
An early paper examining the trade-off was Taylor (1979). The volume edited by Bryant, Hooper and Mann (1993b) extensively examines the issue. [6]
See, for example, Black, Macklem and Rose (1997) for Canada, and Bean (1998) for the UK. [7]
Haldane and Salmon (1995) obtain a similar result for the UK. [8]
In Figure 3, the curves are constructed slightly different to that in Figure 1. The γs in the reaction function are varied, rather than the weight λ in the objective function. [9]
See the discussion in Section 3.1 of de Brouwer and O'Regan (1997) for more detail. [10]