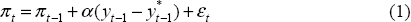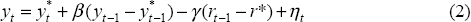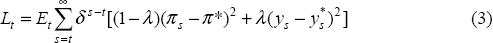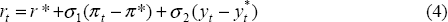RDP 1999-08: Inflation Targeting and Output Stabilisation 2. Theory

The role of output stabilisation in inflation targeting can be illustrated by the following simple model (see Taylor (1994), Svensson (1997a) or Ball (1997)) which consists of a Phillips curve, aggregate demand equation and the central bank's loss function:

where π is inflation, π^* is the inflation target, y is output, y^* is potential output, r is the short-term real interest rate which is assumed to be the instrument of monetary policy, δ is a discount rate, and ε_t and η_t are i.i.d. shocks which are not known to the policy-maker when the interest rate in time t is chosen. r^* is the neutral real interest rate.

Interest rates affect output with a one-period lag, and inflation with a two-period lag indirectly through the impact of interest rates on the output gap. This accords with the lag structure in many economies.

Through the choice of its policy instrument (the real interest rate), the central bank minimises the loss function, which is the weighted sum of inflation and output deviations from their target levels.^[1] Svensson (1997b) interprets the objective function with λ=0 as strict inflation targeting, where no direct concern is paid to output variability. Mervyn King (1997) has referred to a policy-maker with such an objective function as an ‘inflation nutter’. Flexible inflation targeting refers to the case where λ>0. In practice, it appears that all the inflation-targeting central banks have adopted flexible inflation targets to varying degrees.

The model can be solved to yield a reaction function for the central bank of the form:

where σ depends on the parameters in the model, and in particular, the relative weight on output stabilisation in the objective function (λ).

Monetary policy is adjusted in response to deviations of inflation from its target value and output from potential. Such a reaction function for monetary policy is often referred to as a Taylor rule.^[2] In this instance, optimal policy can be described by a simple Taylor-type rule because of the simple structure of the economy. In practice, optimal monetary policy involves examining all available economic information affecting the future values of output and inflation. The inflation target provides the filter with which to process that information.

When λ=0, the optimal policy is straightforward. The instrument is adjusted so that the expected inflation rate two periods hence, is equal to the target inflation rate π^*. The presence of a two-period lag in the effect of monetary policy on inflation means that the optimal policy corresponds to inflation forecast targeting. In this sense, Svensson (1997a) has referred to the inflation forecast as the intermediate target of policy.

When there is positive weight on output stabilisation (λ>0), the optimal solution is to set the interest rate to only partially close the gap between expected inflation (the inflation forecast) and the inflation target two periods hence. The gradual closing of the inflation gap reduces the fluctuations in output.

Note that even with strict inflation targeting (λ=0), there is still a positive weight on output in the monetary policy reaction function. This is because of the information content of the output gap for the forecast of inflation.

The interaction between output and inflation and the consequent effects on their respective variabilities can be illustrated by considering the impact of the two shocks in the model. Ball (1997) and Svensson (1997b) discuss this in more detail.

Firstly, consider a positive demand shock (η_t>0) that increases output above potential, which, in the following period, leads to an increase in inflation. The policy response in this case is to increase interest rates to counteract the inflationary impulse. The extent to which interest rates are adjusted will depend on the relative weight on output stabilisation in the loss function. The higher the weight on output, the smaller the interest rate response. A smaller interest rate response decreases the variability in output but increases the extent to which inflation remains above target, increasing inflation variability.

In general, both the shape and position of the trade-off between output and inflation variability may be affected by the design of the inflation-targeting framework. This is discussed in more detail in Section 5.

Note that the above variability trade-off arises because of the differing lags between the impact of a change in interest rates on output and inflation. Absent the lag structure, the weight on output stabilisation would be irrelevant in the case of a demand shock; interest rates would be adjusted to close the output gap, returning output and inflation to target immediately. In this case, there is no trade-off between output and inflation variability.

Secondly, consider a supply shock (ε_t>0) that increases inflation only, output remains at potential. Regardless of the lag structure, there is a trade-off between output and inflation variability. A negative output gap is required to return inflation to its target rate. The larger the output gap generated, the quicker inflation returns to target, thereby decreasing inflation variability but at the expense of increased output variability.

Again, as was the case with a demand shock, the impact of small supply shocks can be accommodated by appropriate design of the inflation-targeting framework. However, large negative supply shocks that result in a large increase in the price level and the inflation rate, and possibly also open up a negative output gap create more difficulties for the policy-maker. Some trade-off between inflation and output variability is unavoidable.

The trade-off between inflation and output variability can be made starker if we consider a slightly modified model where the transmission of monetary policy changes to inflation is particularly rapid. For example, assume that changes in short-term interest rates result in immediate changes in the exchange rate which are rapidly passed through to consumer prices.^[3]

In response to a deviation of inflation from target, interest rates could be adjusted by an amount large enough to engender a sufficient movement in the exchange rate to return inflation to its target rate almost immediately. While this might be feasible, it may not be desirable, if (as is the case in many countries) the required movement in interest rates and the exchange rate are destabilising for the real economy. The volatility of interest rates and the exchange rate would also increase substantially, raising the prospect of instrument instability.

In conclusion, output stabilisation clearly has a role to play in inflation targeting. The critical question is how large a role should it have. The answer is essentially an empirical issue. Before turning to the empirical evidence however, the next section makes a short digression to consider the variability trade-off in more detail.

Footnotes

An interest rate smoothing term is often also included in the objective function. See Lowe and Ellis (1997) for a discussion of the rationale for interest rate smoothing. [1]

Taylor (1993) found that assigning the weight of 0.5 to both σ₁ and σ₂ resulted in a reaction function that provided a good approximation of the actions of the Federal Reserve. [2]

Bharucha and Kent (1998), Svensson (1998) and Ball (1998) all consider an open economy version of the above model that incorporate this feature. [3]