RDP 2005-09: The US Current Account Deficit: A Re-Examination of the Role of Private Saving 4. Model Simulations

4.1 Current Account

We ask what the consequences are if the US consumer is expecting an increase in the US's share of net world GDP. Specifically, we ask what the effects are of an expectation of an increase from its current share, γ_t, to some larger share, 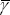. We assume that the shares will evolve in an autoregressive fashion, with α determining the degree of serial correlation. In particular, if α is large (close to one), then the growth in the GDP share will be slow.

This model of GDP shares is given in Equation (9). We can use the result of Equation (10) to substitute into Equation (12) and get:

Note that the solution for the current account to GDP ratio does not depend on the absolute value of the GDP shares, but only the ratio of the long-run to the current GDP share. So, the calibration does not depend on any measure of the US's current share, but only on how much its share is expected to increase.

This equation can be inverted to ask what assumption about the long-run increase in the US share of adjusted GDP could account for a current account deficit of 6 or 7 per cent of (net) GDP. The deficit at the beginning of 2004 was around 7 per cent. We get:

Following usual calibration exercises, we will assume the annual discount factor in utility is β = 0.98. If the increase in output shares is very gradual, so that α = 0.95, we find that in order to have 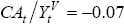, we need 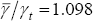. That is, if the US expects a gradual 10 per cent (not 10 percentage points) increase in its share of world GDP, then a current account deficit of 7 per cent of (net) GDP can be optimal.

That seems like a very large increase in the output share, but it is approximately the size of the increase the US has experienced over the past 15 years, according to Figure 1. If the US share is going to gradually rise by this much, with an autoregressive coefficient of 0.95, then the growth over the next 25 years in the share would need to be about 7.1 per cent. That is, if US consumers are expecting the share of US net GDP to grow by 7.1 per cent over the next 25 years (with an eventual cumulative growth of 9.8 per cent), then the entire current account deficit of the US could be explained by optimal consumption behaviour, without any reference to investment spending or government spending.

But Figure 1 only records the US share of adjusted G7 GDP. It may be less plausible that the US share would grow as fast if it were compared to world GDP. On the other hand, we have noted that some of the fastest growing countries in the rest of the world have high saving rates, so that their current accounts are actually in surplus. If their saving rates were to remain high, then the US deficit now may be optimal even if the US share of world output is not expected to grow. For example, if we use Equation (22) to assess this possibility, then assuming β = 0.98 but only a slightly higher level for β*, the model predicts a current account deficit of 7 per cent of (net) GDP. Specifically, we need 1 − β/1 − β^W = 1.07, which implies a value of β^W = 0.9813. If US GDP is approximately 20 per cent of world GDP, then the rest of the world's discount factor would need to equal 0.9816. That is, only a small difference between the US and rest of world discount factor is needed to account for a large current account deficit.

4.2 Real Exchange Rate

Now suppose we take it as given that the assumption that the long-term growth in the US share is given by 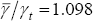so that 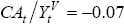is optimal (with no difference in discount factors between US and foreign households). What will the evolution of prices look like in such a model?

In addition to assuming β = 0.98 and α = 0.95, we need to make assumptions regarding the degree of home bias in consumption of traded goods, the share of non-traded goods in consumption, and the elasticity of substitution between home and foreign goods. We choose these to be θ = 0.7, δ = 0.75 and ε = 6, respectively, to match the assumptions of Obstfeld and Rogoff (2004).

As we have discussed above, the calibration of the real exchange rate depends on the model that we use for output growth. In the endowment model, we must make an assumption about 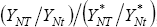, the growth rate of the home endowment of the non-traded good compared to the foreign endowment. Let us suppose that the horizon for comparison is 10 years – we would like to know what the change in the US real exchange rate will be over the next 10 years. In an endowment model, a generous assumption would be that the US non-traded share would rise relative to the foreign non-traded share by 10 per cent in 10 years. Under that assumption, the overall real depreciation for the US in 10 years will be only 15.5 per cent.

If instead we take a model in which factors are mobile between the sectors that produce traded goods and non-traded goods within each country, then Equation (52) determines the real depreciation over this period. As we have noted, this model could conclude that there will be a real appreciation rather than a real depreciation for the US. As in the Balassa-Samuelson model, if the US's traded sector is more productive, then the relative price of its non-traded goods will rise. Working in the other direction are the economic forces that tend to drive the prices of US traded goods down relative to the prices of traded goods in the rest of the world.

We must make an assumption about the magnitude of the change in 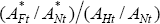: the productivity of the rest of the world's traded sector relative to its non-traded sector, compared in turn to the same productivity ratio in the US. We will assume that the US traded sector shows a 10 per cent improvement compared to the rest of the world over the next 10 years. Under this assumption, there is virtually no change in the US real exchange rate. The model implies a real appreciation of 0.7 per cent over 10 years.

So, contrary to the findings of Obstfeld and Rogoff (2004), if the US current account deficit reflects expectations of an increase in the US's future share of world GDP, and if the reduction of the US current account deficit occurs as part of an optimal adjustment path, then the required change in the US real exchange rate might be quite small.