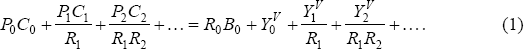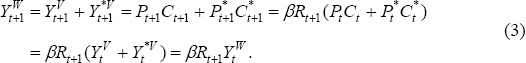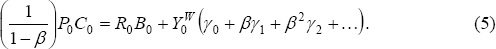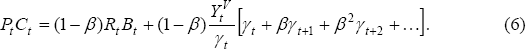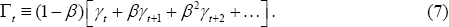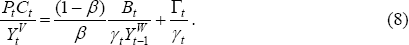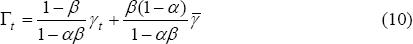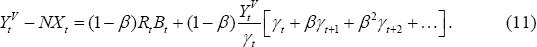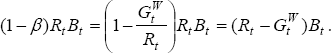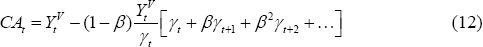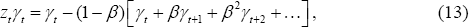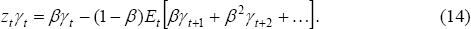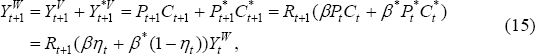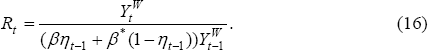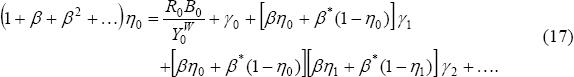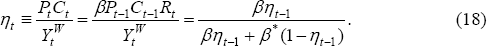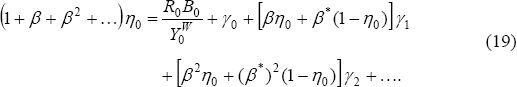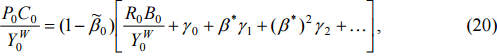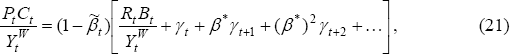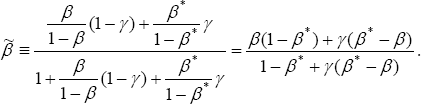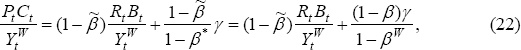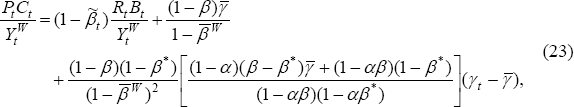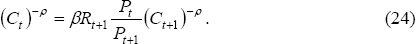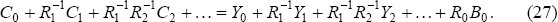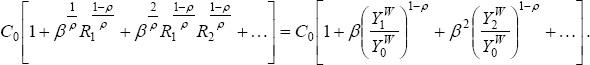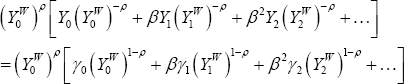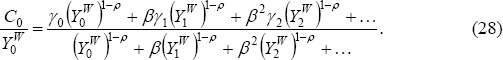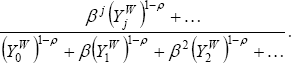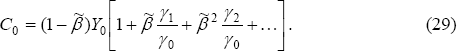RDP 2005-09: The US Current Account Deficit: A Re-Examination of the Role of Private Saving 2. The Model

We build a two-country general equilibrium model in which households choose consumption optimally over an infinite horizon. We begin with the case in which households in each country discount future utility by the same factor, β (where 0 < β ≤ 1), and utility of aggregate consumption is logarithmic (implying a unitary intertemporal elasticity of substitution). We examine the model under the assumption of perfect foresight.

2.1 Equal Discount Factors, Logarithmic Utility

In general, if preferences are homothetic, we can write a household's total nominal expenditure on consumption as P_tC_it, where P_t is the exact consumer price index, and C_it is the real consumption bundle for household i. If we assume that there are N identical households in the home country, then the total national nominal expenditure is P_tC_t, where P_t is the exact consumer price index, and C_t ≡ N⋅C_it is the aggregate real consumption index. We can also use the notation 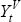to be the total nominal value of output in the home country, net of investment and government spending. (We use V as the superscript to denote ‘value’.) The corresponding variables for the foreign country are labelled with a ‘*’.

The model we examine is one in which only real values are determined. It is helpful to maintain the notion that prices are expressed in terms of a currency, because then the symmetry between the home and foreign countries will be clearer. But we should interpret all nominal prices as being expressed in a common currency, as if these two countries were in a currency union. To reiterate, this is merely notational convenience, and has no implications for the results in the model.

We have not assumed that preferences are identical between the home and foreign country. A household could, for example, have a home bias in consumption, whereby it gives greater weight in preferences to goods produced in its own country. There could be non-traded goods, so that only home-country households consume home-country non-traded goods, and likewise for foreign households. All that we require is that preferences be homothetic, so that we can define consumption aggregates for each household and their exact price index.

We can aggregate across the budget constraint for each household in the home country to write:

Here, R_t is the gross nominal interest rate for period t. B_t is the home country's nominal claims on the foreign country at time t (so that if the home country is a debtor, B_t is negative). The Euler equation for consumption is given by:

Using this equation and its foreign counterpart, we get:

In this derivation we have used the equilibrium condition that the total value of world consumption is equal to the total value of world output (net of investment and government spending) in each period. We use the notation 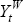to denote the value of world output at time t. From Equation (3) it follows that:

Substituting Equations (2) and (4) into (1), we get:

Here, 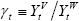is the home country's share of world net GDP at time t. We can rewrite this equation slightly, and express nominal consumption at time t as:

This is the key equation of our model. It says that the consumption/output ratio for a country will depend on the discounted sum of its current and future share of world net GDP, relative to its current share. To see this, define the present value relationship:

Then we can write Equation (6) as:

(We have used Equation (4) to substitute out for the equilibrium interest rate.)

Equation (8) tells us that the home country will tend to have a high ratio of current consumption to output when its expected discounted current and future shares of world net GDP, Γ_t, is high relative to its current share of world net GDP, γ_t . The interest rate does not appear in Equation (8), since it can be solved for in terms of the growth rate of world output (and the discount factor) according to Equation (4). The relationship in Equation (8) could be consistent with any world growth rate. That is, what matters for the country's consumption/output ratio is its current and expected future shares of world output. The higher is its future share of world output compared to its current share, the greater will be its consumption/output ratio. That is true whether its share of world output is rising because its own output is rising faster than the rest of the world's output is rising, or it is falling less quickly than the rest of the world's output is falling.

To see how growth in the share of world income might matter, consider this simple autoregressive model for the home country's net GDP share:

Then,

so the discounted sum of the current and future shares, Γ_t, is a weighted average of the current share and the long-run steady-state share, 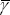. The more weight that individuals put on the future in their utility (larger β) or the faster the convergence to the steady-state value (smaller α), then the greater the importance of the long-run output share in determining current consumption.

To get to the empirical model that we will examine in our Carnegie-Rochester paper, we use the national income accounting identity, 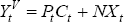, where NX_t is the home country's net export of goods and services (not including interest payments on its debt). We can rewrite Equation (6) above as:

The current account is given by CA_t = NX_t + (R_t − 1)B_t. We propose the following approximation: CA_t ≈ NX_t + (1 − β)R_tB_t. Obviously this is not exact, but how far off is it? That is, how close is (1 − β)R_tB_t to (R_t − 1)B_t ? From the solution for the interest rate above, we have that 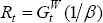, where 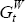is the growth rate of world output. Then,

If 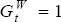, the approximation would be exact. But we believe the difference between CA_t = NX_t + (R_t − 1)B_t and 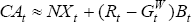is small, so the approximation is reasonable. With this approximation, we can then rewrite the model as:

Or

where .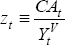

We have derived all of this under perfect foresight. Now we arbitrarily incorporate an expectations sign in Equation (13), to get:

If we had derived the model from the beginning under the assumption of uncertainty, then Equation (14) would not hold exactly. So Equation (14) is not, strictly speaking, derived from the Euler equation under uncertainty and the rest of the model. Perhaps future work can assess the error involved with the approximations used to derive Equation (14).

Equation (14) implies a relationship between a country's current account relative to world net GDP (z_tγ_t) and the country's current and expected future shares of world net GDP.

2.2 Different Discount Factors, Logarithmic Utility

Here we briefly consider how Equation (14) would look if the discount factor in each country were different. This is a simple way to capture the notion that some countries which have very good growth prospects still tend to have high saving rates. Equations (1) and (2) still hold, but Equation (3) is replaced by:

where 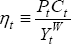. Then, Equation (4) is replaced by:

So we can replace Equation (6) with:

But we can see that:

Substituting into Equation (17):

Solving out for η₀, we have:

where 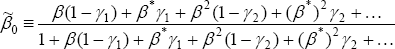. Or, for any time t:

where .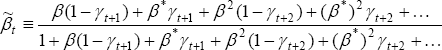

In general, 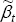is not constant over time. It is interesting, however, to see what the model implies about the special case when each country's share is constant over time. Then we have:

From Equation (21), it follows in this case (setting β_t = 0) that:

where β^W = γβ + (1 − γ)β*. Compared to the case of equal discount factors (β_t = 0), we can now see that the home country's consumption will be higher if it is less patient (has a lower discount factor) than the rest of world.

Another interesting case is when the country's share of world net GDP evolves according to Equation (9). Although the expression for 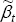is quite complex, and the closed-form solution for Equation (21) is not that intuitive, we can take a linear approximation to the solution around the point :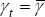

where 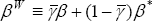. To understand this equation, begin by noting that if the share were constant over time so 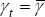, then Equation (23) would reduce to Equation (22). Also note that if the discount factors were equal, but the shares were not constant over time, Equation (23) would reduce to Equation (6), with the solution for Γ_t from Equation (10) substituted in.

2.3 Same Discount Factors, Non-logarithmic Utility

Let the utility function each period be given by (1/(1 − ρ))(C_t)^1−ρ. Then the first-order condition becomes:

In general, we cannot derive anything except in the simple case where there is a single homogenous good that is freely traded and consumed in both countries. In that case, we might as well take the price as constant. So we can rewrite Equation (24) as:

Adding the equivalent expression for foreign consumption, and using the world equilibrium condition, we get:

The home country's budget constraint is:

We can use Equations (25) and (26) to write the left-hand side of Equation (27) as:

The discounted sum of GDP on the right-hand side of Equation (27) can be written as:

Set initial debt to zero so that the expression is easier to look at. Then we can solve Equation (27) as follows:

In this case, initial consumption relative to world income is still a weighted average of current and future shares of world income. Now the weight given on our share in period j is given by:

Suppose the growth rate of world income is constant. Then we can rewrite Equation (28) as simply:

This is identical to the expression we had in the case of unit intertemporal elasticity of substitution, Equation (12), except that the discount factor, β, in Equation (12) is replaced by:

where 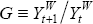Assuming G > 1, we have 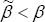if ρ > 1. So, if the intertemporal elasticity of substitution is less than one (that is, ρ > 1), then the weight on future shares is lower compared to the model which assumes that utility is logarithmic.

While we are unable to generalise beyond the case of a single homogenous good when the intertemporal rate of substitution is not unity (that is, utility is not logarithmic), we get the general lesson that if ρ > 1 and the world growth rate is positive, then households effectively discount future shares at a greater rate than implied simply by the discount rate in utility.