RDP 2006-01: Modelling Manufactured Exports: Evidence from Australian States 5. Results

5.1 Mean-group Panel

Estimates of the long-run elasticities from the mean-group panel are given in Table 5. In general, the estimates are relatively consistent using either the DOLS or ADL model (although the standard errors on the price elasticity are generally larger for the ADL model and are therefore typically insignificant). The exceptions are for NSW and Western Australia, with price and income elasticities varying considerably across models. Using the DOLS model, estimates of the price elasticity of manufactured exports range from −0.3 for Western Australia to −0.8 for NSW, but only the coefficients for NSW and Victoria are statistically different (using a Wald test). Estimated income elasticities are between 2.1 and 2.3, but the South Australian elasticity is significantly larger at 3.9.

Table 5: Estimated Elasticity of Manufactured Exports

	Vic	NSW	SA	WA	Q1d	Australia
Price elasticity
DOLS	−0.36**	−0.77**	−0.67**	−0.31*	−0.57**	−0.54**
	(0.12)	(0.21)	(0.28)	(0.17)	(0.16)	(0.16)
ADL	−0.27	−0.26	−0.73**	0.06	−0.51	−0.33
	(0.17)	(0.43)	(0.16)	(0.29)	(0.30)	(0.27)
Income elasticity
DOLS	2.37**	2.15**	3.89**	2.18**	2.31**	2.53**
	(0.07)	(0.14)	(0.11)	(0.10)	(0.11)	(0.10)
ADL	2.15**	1.60**	3.62**	1.68**	2.56**	2.22**
	(0.21)	(0.28)	(0.17)	(0.27)	(0.31)	(0.23)
Diagnostics
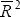DOLS	0.97	0.91	0.97	0.80	0.92
ADL	0.99	0.96	0.97	0.84	0.95
LM (serial correlation, ADL)	3.75	6.02	3.41	0.50	3.88
	[0.15]	[0.05]	[0.18]	[0.78]	[0.14]
Notes: * and ** denote significance at the 10 and 5 per cent levels respectively. Figures in parentheses represent standard errors; those estimated using the DOLS specification use the Newey-West correction. Australian elasticities and standard errors are calculated using the mean-group method. LM (serial correlation) refers to the Breusch-Godfrey LM test (number of observations x R2 statistic), with p-values in square brackets.

The mean-group estimates of the national elasticities are shown in the final column of Table 5. The estimated national price elasticity is −0.5 using the DOLS model and −0.3 using the ADL model, with the latter insignificant due to the wider confidence intervals of the ADL estimates. These elasticities are smaller than those of Dvornak et al (2005), who find an elasticity of −0.8, and may reflect their use of export unit values as the deflator for their real exchange rate (which could bias the estimate towards 1). The estimated national income elasticity is 2.5 using the DOLS model and 2.2 using the ADL model, which are considerably larger than those in previous studies; Caporale and Chui's (1999) estimate (using total exports) is the largest known estimate of the income elasticity of Australian exports at 1.3. It is likely that the considerably higher estimate in this paper stems from the shorter sample used here, with global trade in manufactured exports accelerating during the 1990s following the dismantling of barriers to trade in the 1980s.^[10] This is consistent with the findings of Wu (2005), who estimates an income elasticity of 1.2 for Australian exports over a sample from 1960 to 1998, but an elasticity of 1.9 over the period from 1988 to 1998.

5.2 Robustness Checks

Section 2 highlighted the apparent sensitivity of previous direct Australian estimates of the export price and income elasticity to changes in the specification or estimator used. Given this sensitivity, it is appropriate to check whether the fixed-effects estimation used in this paper provides more robust results.

Three robustness checks were performed on the DOLS model, and two of these are repeated on the ADL model. First, the DOLS model is estimated without including leads of the first differenced regressors. The inclusion of leads in the DOLS model is intended to account for the possible endogeneity of the regressors, which is not expected to be of much importance in this sample, given that manufactured exports in any particular state are likely to have little influence on Australian dollar exchange rates. Consequently, estimating the model without leads may provide a more parsimonious model, at little cost. The second check is to include a trend term in the specification of the DOLS and ADL models. This variable is intended to proxy the increasing integration of global manufacturing trade during the 1990s following the dismantling of trade barriers. Third, the DOLS and ADL models are augmented with a measure of the capital stock in the manufacturing sector. This appears to be a reasonable proxy for the extent of vertical and/or horizontal integration (Krugman 1989 and Grossman and Helpman 1991).^[11]

The baseline DOLS estimates are robust to the exclusion of leads of the regressors in all states, with the mean-group estimates of the price and income elasticities falling only marginally from the baseline specification (Table 6). Similarly, the price elasticity estimates are also quite robust to the inclusion of a time trend; while the change in price elasticity estimates is quite large for some states (such as NSW), the new estimates are rarely outside their previous confidence intervals, and the mean-group estimate declines (in absolute value) by only 0.1 using the DOLS model (and increases marginally using the ADL model). Similar results are also found when the capital stock is included, although the (absolute) decline is somewhat more pronounced.

Table 6: Alternative Estimates of the Elasticity of Manufactured Exports

	DOLS model			ADL model
	Price elasticity	Income elasticity		Price elasticity	Income elasticity
Baseline	−0.54**	2.53**		−0.33	2.22**
Excluding leads	−0.49**	2.47**		na	na
Including trend	−0.39**	4.93**		−0.35**	4.58**
Including capital stock	−0.33**	3.75**		−0.31	3.32**
Notes: ** represents significance at the 5 per cent level, with standard errors on the DOLS model calculated using the Newey-West correction. Elasticities are the mean-group estimate of the national elasticity. The baseline model for the DOLS and ADL specification is the mean-group estimates from Equations (4) and (5) respectively.

In contrast, estimates of the income elasticity are quite sensitive to the inclusion of a time trend or the capital stock. Under these alternative specifications, the income elasticities increase for all states except South Australia, and the mean-group estimate of the income elasticity rises to implausibly large levels. Interestingly, the coefficients on the trend term and the capital stock is negative for all states except South Australia – in contrast to its expected sign – with the estimates implying a trend decline in exports of around 8 per cent per annum (absent trading partner growth).

5.3 Fixed-effects Panel

Given the similarity of the estimated elasticities across states, it is reasonable to estimate a fixed-effects panel that constrains these elasticities to be the same across states. To ensure stationary errors in the South Australian equation, the estimated panel DOLS model (but not the ADL) includes a trend term; otherwise the model is as represented in Equation (4), with long-run coefficients constrained to be identical across states.

Results from the fixed-effects model are generally consistent with the mean-group estimates. In the baseline DOLS specification, the price elasticity of −0.53 is very similar to the estimate from the DOLS mean-group estimate, although the income elasticity is slightly lower at 2.26 (Table 7). The price elasticity estimated from the ADL model is similar in magnitude to that using the DOLS specification and is larger than that found with the mean-group estimator, but not statistically so, while the income elasticity estimate is little changed. This similarity of elasticities according to the two models, and the stationary errors that arise from the fixed-effects estimation, suggest that there is little heterogeneity in the true long-run income and price elasticities (with the exception of the South Australian income elasticity, which is constrained in the DOLS specification by the use of a time trend).

Table 7: Fixed-effects Panel Models

	Price elasticity	Income elasticity
Panel DOLS	−0.53** (0.09)	2.26** (0.07)
Panel ADL	−0.62** (0.10)	2.51** (0.11)
DOLS excluding leads	−0.49** (0.09)	2.24** (0.07)
DOLS including trend	−0.42** (0.09)	4.57** (0.48)
DOLS including capital stock	−0.37** (0.11)	3.56** (0.32)
Notes: ** represents significance at the 5 per cent level. Figures in parentheses are standard errors, estimated using a Newey-West correction. All models include a trend in the South Australian equation to ensure cointegration.

The fixed-effects estimates of the price elasticity are again relatively robust to changes in the specification. As with the mean-group estimates, there is little difference when leads of the regressors are excluded. The price elasticity is somewhat more affected by the inclusion of a trend or the capital stock in the equation, but these new estimates are not statistically different to those previously. In contrast, the income elasticity estimates continue to be significantly affected by the inclusion of a time trend or the capital stock, rising to 4.6 and 3.6 respectively.

5.4 Direct Australian Estimates

Given the focus of this paper has been to estimate the national price and income elasticity of manufactured exports, it is a useful comparison to consider direct estimates of these coefficients. To ensure comparability, the same DOLS and ADL models are estimated on Australian data. Trading partner weights used to construct the real effective exchange rate and foreign income are manufacturing-specific.

The results of the baseline DOLS and ADL models are shown in the top half of Table 8. The elasticity estimates from these models are consistent with those from the panel estimates. The price elasticity estimate according to the DOLS model is slightly lower in absolute value than in the panel estimation (shown in Table 5), while the ADL estimate is slightly higher in absolute value (and significant). The income elasticity estimates in each model are slightly higher than those of the panel specification. The bottom half of the table indicates that the direct estimates of the income elasticity continue to suffer from instability when a time trend or the capital stock are included, in line with the panel results.

Table 8: Direct Estimates of National Export Elasticities

	Price elasticity	Income elasticity		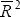	LM
DOLS	−0.46** (0.08)	2.75** (0.05)		0.98
ADL	−0.39** (0.16)	2.58** (0.14)		0.99	2.73 [0.25]
	DOLS model			ADL model
	Price elasticity	Income elasticity		Price elasticity	Income elasticity
Excluding leads	−0.44**	2.71**		na	na
Including trend	−0.38**	4.58**		−0.34**	3.50**
Including capital stock	−0.37**	3.43**		−0.38**	4.94**
Notes: ** represents significance at the 5 per cent level. Figures in parentheses represent standard errors; those estimated using the DOLS specification use the Newey-West correction. LM (serial correlation) refers to the Breusch-Godfrey LM test (number of observations x R2 statistic), with the p-value in square brackets.

Footnotes

It may also be due, in part, to the increasing share of manufactured exports in global trade, underpinned by increasing product variety or quality (Krugman 1989 and Grossman and Helpman 1991). [10]

Krugman and Gross and Helpman argue that vertical integration (increasing the variety of products) and/or horizontal integration (increasing the quality of products) can introduce an upwards bias to estimates of the income elasticity of exports. The use of the capital stock to proxy this effect is due to Muscatelli, Stevenson and Montagna (1995). [11]