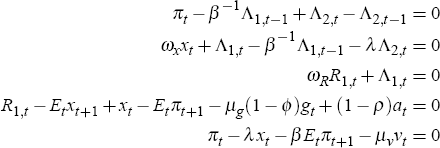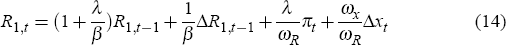RDP 2006-02: Term Structure Rules for Monetary Policy 4. Optimal Monetary Policy Rules
April 2006
- Download the Paper 316KB
I start by constructing an optimal policy rule following Giannoni and Woodford (2002). I consider a rule that would bring about the optimal response to shocks as well as yield a unique stationary equilibrium for the economy. I assume that the objective of the monetary authority is to minimise the expected value of a loss criterium given by
where the bank's discount rate β is the same as in Equation (3) and the period loss function is of the form
Here, the parameters ωx and ωR (assumed to
be positive) govern the relative concern for output and short-term nominal interest rate
variability. The monetary authority faces the problem of minimising the loss function given by
Equation (12) subject to the New IS and Phillips curves given by Equations (1) and (3),
respectively. Notice that minimisation is achieved by choosing a time path for  that
minimises the monetary authority's objective and simultaneously satisfies the model's
structural equations at each point in time. The first-order conditions of the problem are given
by
that
minimises the monetary authority's objective and simultaneously satisfies the model's
structural equations at each point in time. The first-order conditions of the problem are given
by
where Λ1,t and Λ2,t stand for the Lagrange multipliers associated with the IS and New Phillips curve equations respectively. One can use the equations above to substitute out the Lagrange multipliers in order to obtain a monetary policy rule consistent with the optimal solution of the form
As shown by Giannoni and Woodford (2002), commitment to this rule implies a unique equilibrium as well as an optimal pattern of responses to the economy's disturbances. In this case, the optimisation is not performed over some parametric set of policy rules (for example, a Taylor-type rule). Instead, the approach underlying Equation (14) characterises the optimal response to shocks by taking the structural equations as constraints, and then finds the policy rule that generates such an equilibrium.
Any rule constrained to belong to a given set of rules cannot perform better than this optimal rule. Hence, type-1 or type-2 rules could not possibly yield a better outcome than Equation (14). However, studying how close these rules come to the optimal response remains important for many reasons. McCallum's (1988) critique, namely that the main problem that policy-makers face is uncertainty about the exact structure of the economy, implies uncertainty about the exact specification of the optimal monetary policy rule. For this reason it remains important to understand how a given rule works across different plausible environments. Simple policy rules have also been proposed on the basis of being operational and simple to communicate to the public. Operational considerations suggest that rules should be expressed in terms of instrument variables that can be controlled by central banks and require only information available to central banks.[20] Recall that the outcome of any type-2 rule can be reproduced by some rule for the short-term rate. So implementation of type-2 rules need not require modifications of operating procedures.
I therefore consider the optimal rule, Equation (14), as a benchmark to evaluate the performance of type-1 and type-2 rules (restricting attention to those that result in a unique REE). For reference, I also examine outcomes based on the standard Taylor rule.
4.1 Type-1 Rules
Table 1 shows, for different calibrations of ωx and a value of 0.1 for ωR, the value of the loss function and each of its components for the optimal rule (Equation (14)), the standard Taylor rule (Equation (4)), and type-1 rules of the selected term structure.[21]
| Optimal rule | Taylor rule | R2 | R4 | R12 | R20 | R40 | |
|---|---|---|---|---|---|---|---|
| ωx = 0.1 | |||||||
| Loss | 0.9926 | 1.0032 | 1.0032 | 1.0032 | 1.0032 | 1.0032 | 1.0032 |
| Var(π) | 0.1015 | 0.1147 | 0.1147 | 0.1147 | 0.1147 | 0.1147 | 0.1147 |
| Var(x) | 8.8961 | 8.8824 | 8.8824 | 8.8824 | 8.8824 | 8.8824 | 8.8824 |
| Var(R1) | 0.0150 | 0.0031 | 0.0031 | 0.0031 | 0.0031 | 0.0031 | 0.0031 |
| ωx = 0.33 | |||||||
| Loss | 2.8191 | 2.8744 | 2.8744 | 2.8744 | 2.8744 | 2.8744 | 2.8744 |
| Var(π) | 0.4574 | 0.3616 | 0.3614 | 0.3614 | 0.3614 | 0.3614 | 0.3614 |
| Var(x) | 7.0625 | 7.5377 | 7.5383 | 7.5383 | 7.5382 | 7.5383 | 7.5383 |
| Var(R1) | 0.0757 | 0.0027 | 0.0027 | 0.0027 | 0.0027 | 0.0027 | 0.0027 |
| ωx = 1 | |||||||
| Loss | 6.7243 | 7.5900 | 7.5900 | 7.5900 | 7.5900 | 7.5900 | 7.5900 |
| Var(π) | 1.6088 | 0.8299 | 0.8299 | 0.8301 | 0.8299 | 0.8299 | 0.8299 |
| Var(x) | 5.0405 | 6.7488 | 6.7488 | 6.7486 | 6.7488 | 6.7488 | 6.7488 |
| Var(R1) | 0.7504 | 0.1130 | 0.1130 | 0.1130 | 0.1130 | 0.1130 | 0.1130 |
| ωx = 3 | |||||||
| Loss | 14.2980 | 19.5110 | 19.5110 | 19.5110 | 19.5110 | 19.5110 | 19.5110 |
| Var(π) | 4.8407 | 3.7726 | 3.7726 | 3.7725 | 3.7726 | 3.7726 | 3.7726 |
| Var(x) | 3.0422 | 5.1710 | 5.1710 | 5.1711 | 5.1710 | 5.1710 | 5.1710 |
| Var(R1) | 3.3090 | 2.2525 | 2.2525 | 2.2524 | 2.2525 | 2.2525 | 2.2525 |
Reacting to movements in nominal longer-term rates does not present significant gains. As expected, type-1 rules are no worse than the standard Taylor rule, since this rule is a particular case of a type-1 rule for which γ is set to zero. Inspection of Table 1 shows not only that type-1 rules achieve a value of the loss function which is identical to that of the Taylor rule, but also that the variances of the relevant variables remain unchanged.[22]
In general, for all calibrations and maturities considered, the optimal value of γ turns out to be negative. This is a surprising result in light of Goodfriend's (1993) account of monetary policy and Mehra's (1999) econometric results. Recall that the rationale for allowing the monetary authority to react to movements in long-term bond yields is that long-term nominal interest rates could measure the private sector's long-term inflationary expectations. The central bank might, therefore, be interested in using reaction functions that incorporate longer-term rates, so that if they rise the bank raises the short-term rate in its attempts to keep inflation under control. In other words, this behaviour would imply a positive value of γ.[23]
Since there appear to be no significant gains in reacting to movements in longer-term rates, I do not investigate any further the behaviour of type-1 rules under alternative calibrations for ωx and ωR.
4.2 Type-2 Rules
For different calibrations of ωx and a value of 0.1 for ωR, Table 2 shows the value of the loss function and the value of each of its components for the optimal rule (Equation (14)), the Taylor rule (Equation (4)), and type-2 rule (Equation (6)) for interest rates at selected maturities.
| Optimal rule | Taylor rule | R2 | R4 | R12 | R20 | R40 | |
|---|---|---|---|---|---|---|---|
| ωx = 0.01 | |||||||
| Loss | 0.1167 | 0.1180 | 0.1179 | 0.1177 | 0.1182 | 0.1189 | 0.1195 |
| Var(π) | 0.0039 | 0.0032 | 0.0032 | 0.0032 | 0.0033 | 0.0024 | 0.0012 |
| Var(x) | 11.0347 | 11.2289 | 11.2218 | 11.2058 | 11.1868 | 11.2659 | 11.4064 |
| Var(R1) | 0.0252 | 0.0248 | 0.0245 | 0.0244 | 0.0307 | 0.0386 | 0.0423 |
| ωx = 0.05 | |||||||
| Loss | 0.5287 | 0.5376 | 0.5374 | 0.5370 | 0.5359 | 0.5362 | 0.5377 |
| Var(π) | 0.0396 | 0.0443 | 0.0440 | 0.0435 | 0.0426 | 0.0433 | 0.0453 |
| Var(x) | 9.7381 | 9.8486 | 9.8494 | 9.8505 | 9.8377 | 9.8192 | 9.7952 |
| Var(R1) | 0.0216 | 0.0094 | 0.0095 | 0.0098 | 0.0138 | 0.0194 | 0.0262 |
| ωx = 0.1 | |||||||
| Loss | 0.9926 | 1.0032 | 1.0032 | 1.0029 | 1.0028 | 1.0027 | 1.0035 |
| Var(π) | 0.1015 | 0.1147 | 0.1143 | 0.1134 | 0.1116 | 0.1097 | 0.1110 |
| Var(x) | 8.8961 | 8.8824 | 8.8853 | 8.8917 | 8.9075 | 8.9230 | 8.9173 |
| Var(R1) | 0.0150 | 0.0031 | 0.0031 | 0.0033 | 0.0040 | 0.0063 | 0.0069 |
| ωx = 0.33 | |||||||
| Loss | 2.8191 | 2.8744 | 2.8752 | 2.8766 | 2.8773 | 2.8775 | 2.8778 |
| Var(π) | 0.4574 | 0.3616 | 0.3593 | 0.3562 | 0.3556 | 0.3554 | 0.3515 |
| Var(x) | 7.0625 | 7.5377 | 7.5472 | 7.5612 | 7.5651 | 7.5662 | 7.5789 |
| Var(R1) | 0.0757 | 0.0027 | 0.0019 | 0.0006 | 0.0000 | 0.0000 | 0.0000 |
| ωx = 1 | |||||||
| Loss | 6.7243 | 7.5900 | 7.6189 | 7.6732 | 7.7088 | 7.7089 | 7.7105 |
| Var(π) | 1.6088 | 0.8299 | 0.7823 | 0.6832 | 0.5987 | 0.6066 | 0.6135 |
| Var(x) | 5.0405 | 6.7488 | 6.8280 | 6.9865 | 7.1101 | 7.1023 | 7.0970 |
| Var(R1) | 0.7504 | 0.1130 | 0.0872 | 0.0347 | 0.0000 | 0.0000 | 0.0000 |
| ωx = 3 | |||||||
| Loss | 14.2980 | 19.5110 | 19.8466 | 20.6461 | 21.8445 | 21.9581 | 22.0236 |
| Var(π) | 4.8407 | 3.7726 | 3.5856 | 3.1417 | 5.8654 | 6.0786 | 6.1891 |
| Var(x) | 3.0422 | 5.1710 | 5.3491 | 5.7716 | 5.1613 | 5.1196 | 5.1001 |
| Var(R1) | 3.3090 | 2.2525 | 2.1369 | 1.8943 | 4.9512 | 5.2074 | 5.3430 |
When the concern for the output variance is relatively low, type-2 rules based on rates of longer maturities generally perform better than the Taylor rule. For example, when ωx equals 0.05, all type-2 rules except the one based on R40 do better than the Taylor rule, with the R12 rule being the best among these. Also, note that a type-2 rule based on R12 generates a lower variance for R1 and higher variances for inflation and output relative to the optimal rule, but lower variances of inflation and output relative to the Taylor rule.
When the concern for output volatility increases to 0.1, the best among the type-2 rules shown is that which is based on the 5-year rate. Inspection of Table 2 reveals that in this case the relevant gain comes from the ability of this R20 rule to generate a lower variance of inflation. Observe that when ωx equals 0.01, 0.05 and 0.1 (that is, when the concern for output deviations is relatively low) the variance of the short-term rate increases with the maturity of the interest rate in the rule. For these parameter values, type-2 rules yield a higher variance of the short-term rate than that of the Taylor rule. However, this property is not preserved when the concern for output deviations increases to ⅓ or to 1.
Table 3 reproduces the results of Table 2 but this time with ωR set to 1. With this greater aversion to the variance of the short-term interest rate, the variance of R1 is reduced in all cases and for all rules. In Table 3, for all values of ωx considered, the variance of the short-term rate achieved by type-2 rules is lower than it is for the optimal rule case and for the Taylor rule.[24]
| Optimal rule | Taylor rule | R2 | R4 | R12 | R20 | R40 | |
|---|---|---|---|---|---|---|---|
| ωx = 0.01 | |||||||
| Loss | 0.1280 | 0.1289 | 0.1288 | 0.1287 | 0.1306 | 0.1335 | 0.1366 |
| Var(π) | 0.0128 | 0.0129 | 0.0128 | 0.0127 | 0.0156 | 0.0199 | 0.0254 |
| Var(x) | 10.9092 | 10.9984 | 10.9958 | 10.9874 | 10.9132 | 10.8553 | 10.7963 |
| Var(R1) | 0.0062 | 0.0061 | 0.0061 | 0.0061 | 0.0058 | 0.0050 | 0.0032 |
| ωx = 0.05 | |||||||
| Loss | 0.5375 | 0.5419 | 0.5418 | 0.5415 | 0.5415 | 0.5426 | 0.5440 |
| Var(π) | 0.0479 | 0.0522 | 0.0520 | 0.0515 | 0.0522 | 0.0549 | 0.0584 |
| Var(x) | 9.7043 | 9.7458 | 9.7472 | 9.7488 | 9.7300 | 9.7017 | 9.6733 |
| Var(R1) | 0.0044 | 0.0024 | 0.0024 | 0.0026 | 0.0028 | 0.0026 | 0.0018 |
| ωx = 0.1 | |||||||
| Loss | 0.9993 | 1.0047 | 1.0046 | 1.0045 | 1.0044 | 1.0048 | 1.0053 |
| Var(π) | 0.1090 | 0.1183 | 0.1181 | 0.1175 | 0.1166 | 0.1175 | 0.1193 |
| Var(x) | 8.8679 | 8.8555 | 8.8571 | 8.8607 | 8.8685 | 8.8638 | 8.8538 |
| Var(R1) | 0.0035 | 0.0008 | 0.0008 | 0.0009 | 0.0010 | 0.0009 | 0.0006 |
| ωx = 0.33 | |||||||
| Loss | 2.8492 | 2.8757 | 2.8762 | 2.8769 | 2.8773 | 2.8778 | 2.8780 |
| Var(π) | 0.3916 | 0.3581 | 0.3572 | 0.3558 | 0.3555 | 0.3509 | 0.3553 |
| Var(x) | 7.3225 | 7.5506 | 7.5554 | 7.5629 | 7.5656 | 7.5806 | 7.5684 |
| Var(R1) | 0.0167 | 0.0008 | 0.0005 | 0.0002 | 0.0000 | 0.0000 | 0.0000 |
| ωx = 1 | |||||||
| Loss | 7.1171 | 7.6441 | 7.6601 | 7.6891 | 7.7070 | 7.7098 | 7.7104 |
| Var(π) | 1.1005 | 0.6977 | 0.6772 | 0.6367 | 0.6058 | 0.6064 | 0.6055 |
| Var(x) | 5.7595 | 6.9144 | 6.9589 | 7.0434 | 7.1011 | 7.1034 | 7.1049 |
| Var(R1) | 0.2570 | 0.0320 | 0.0240 | 0.0090 | 0.0000 | 0.0000 | 0.0000 |
| ωx = 3 | |||||||
| Loss | 16.3987 | 20.5962 | 20.8247 | 21.3184 | 21.7777 | 21.7844 | 21.7845 |
| Var(π) | 3.0671 | 1.8028 | 1.6506 | 1.2557 | 0.7568 | 0.7618 | 0.7485 |
| Var(x) | 3.9136 | 6.0524 | 6.2104 | 6.5889 | 7.0070 | 7.0075 | 7.0120 |
| Var(R1) | 1.5907 | 0.6364 | 0.5428 | 0.2960 | 0.0000 | 0.0000 | 0.0000 |
A comparison of Tables 2 and 3 shows that when the concern for output variance is relatively low the optimal type-2 rule (in terms of the maturity of the interest rate) is sensitive to the value of ωR. For example, when ωx equals 0.1 and ωR equals 0.1, the best rule is that based on R20. However, when ωx equals 0.1 and ωR equals 1, the best rule is that based on R12. Despite these differences in the maturity length, Tables 2 and 3 show an interesting pattern. When the relative concern for output volatility is low, medium/long-term rate rules perform better than the Taylor rule, and when the concern for the output variance is high, the Taylor rule turns out to be better. In short, the best rule depends upon the parameters determining the preferences of the monetary authority.
Tables 2 and 3 reveal the presence of two different kinds of trade-offs between the variance of inflation and the variance of output. The first is the well-known Taylor curve trade-off that arises when the parameter that governs the relative degree of concern for the output gap variance, ωx, varies. For all rules considered, as ωx rises from 0.01 to 3, the central bank generates a lower variance for output at the expense of a higher one for inflation.
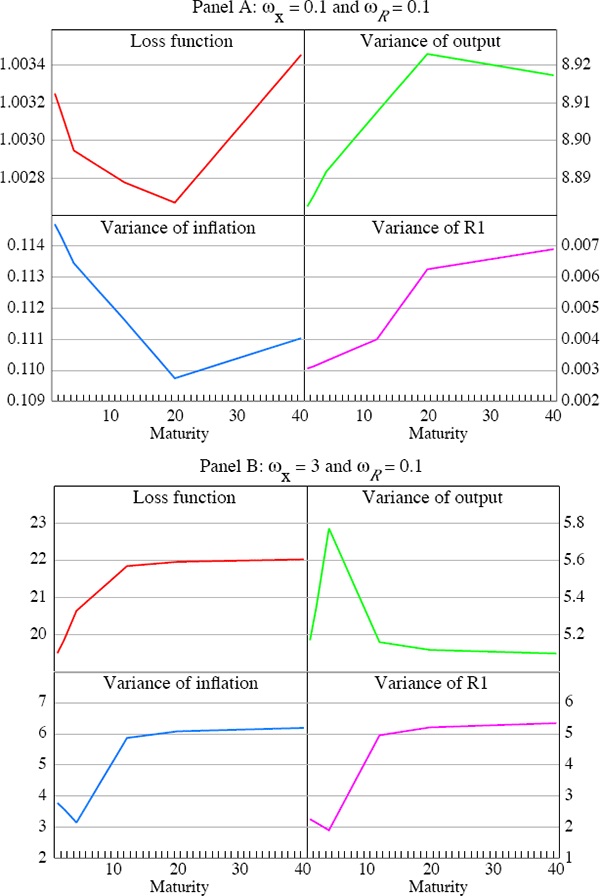
The second trade-off between the variance of output and the variance of inflation, which to the best of my knowledge is new in the literature, shows up in terms of maturities. Notice that a trade-off between the output and inflation variance appears for given values of ωx and ωR as we move along the maturity dimension of the class of type-2 rules. However, this trade-off is not working in the same direction in all cases. For example, it is not always the case that when the maturity length of the type-2 rule increases, one observes a lower variance of inflation at the expense of a higher one for output. Figure 4 illustrates this by plotting the loss function and its components against the maturity of the interest rate in the rule. Panel A plots the case when ωx equals 0.1 and ωR equals 0.1. As the maturity of the interest rate rule increases up to 20, the variance of inflation decreases and the variance of output increases, but as we move further along the term structure the trade-off changes direction. Panel B shows the case when the preferences of the central bank are ωx equals 3 and ωR equals 0.1. In this case the variance of inflation decreases and that of output increases but only up to a maturity of four quarters. The direction of the trade-off changes above this maturity. It is important to emphasise that this is a trade-off that emerges for given values of the parameters that govern the preferences of the monetary authority, ωx and ωR. Also, the precise nature of this trade-off changes when the preferences of the central bank change.
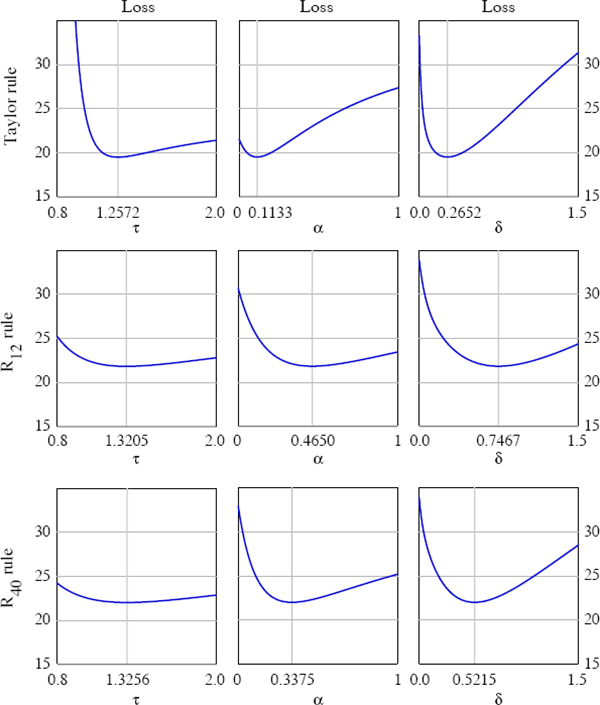
One further feature of type-2 rules is worth highlighting. Compared to the standard Taylor rule, they appear to be more forgiving of deviations from their optimal setting. An example of this is provided in Figure 5, which shows the behaviour of the loss function as we depart from the optimal value of one of the parameters in the policy rule (holding the other parameters at their optimal values). For this particular set of preferences the Taylor rule happens to outperform type-2 rules. Even so, the loss function appears to be flatter for type-2 rules (across a wide range of parameter values). What Figure 5 shows is that it seems relatively less costly for the central bank to deviate from the optimal values of τ, α, and δ using the type-2 rule for R12, as opposed to deviations from the best form of the Taylor rule (or even the type-2 rule for R40). This flatness of type-2 rules is potentially beneficial for policy-makers with some uncertainty about the optimal parameters of a rule.
Footnotes
If the central bank collects data with a lag, then depending on the frequency of the model, the rules described here might not be operational in practice. Notably, McGough et al (2005) address this problem and find regions of uniqueness for policies that set a longer-term rate in response to lagged inflation. [20]
Notice that
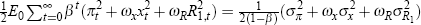 .
So minimising J is equivalent to
minimising a weighted average of the variances as given by
.
So minimising J is equivalent to
minimising a weighted average of the variances as given by 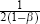
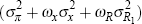 . Since
. Since 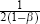 is only a scaling constant, one can focus on the value of
is only a scaling constant, one can focus on the value of
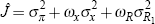 instead. This is the value of the loss function reported in
all tables.
[21]
instead. This is the value of the loss function reported in
all tables.
[21]
This is, in general, true up to the 9th decimal digit. A higher numerical precision shows that type-1 rules are better than the standard rule as one would expect. However, this difference is obviously trivial. [22]
Interestingly, there is recent macro-finance literature that includes the long-run expected inflation component of the long-term rate in the policy rule and can justify negative values for γ. For example, in response to a perceived decrease in the inflation target (a decrease in the expected inflation component of the long rate), the monetary authority must increase rates in order to push inflation down to this lower target. This behaviour would justify a negative value of γ. See Rudebusch and Wu (2004). [23]
This is, in principle, an interesting result in light of the liquidity trap problem. If, instead, one found that for all type-2 rules, the variance of the short-term rate increases, then the chance of hitting the zero lower bound would increase under type-2 rules. [24]