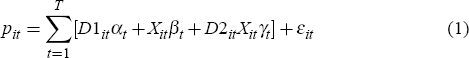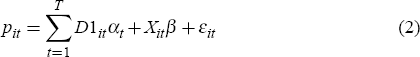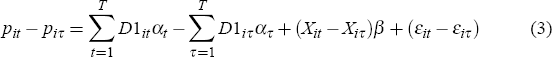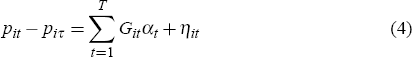RDP 2006-03: Australian House Prices: A Comparison of Hedonic and Repeat-sales Measures 3. Alternative Measures of House Prices

3.1 Hedonic Measures

Hedonic measures have a strong theoretical grounding (see, for example, Griliches 1971 and Rosen 1974) and use regression techniques to control for compositional and quality change. Meese and Wallace (1997) show that a general form of a hedonic specification can be written as follows:

where p_it is the log of the price of house i when sold at time t, D1_it is a time dummy equal to 1 for the i^th house if sold at time t and 0 otherwise, X_it is a vector of house characteristics for house i when sold at time t, D2_it is a vector of dummy variables with 1's for repeat-sales observations and 0's otherwise, and ε_it is white noise. In this model the exponential of (α_t − α₁) provides an estimate of the rate of growth in the mean price with respect to the mean price at the start of the sample period.^[5] Further, β_t provides estimates of the implicit value of the house characteristics at time t. It should be noted that this is a pooled rather than panel data regression, as the number of observations varies with each time period t. The key advantage of the general hedonic formulation is that it provides direct estimates of pure price changes and can, in principle, control for changes in the composition and quality of houses sold.

Nonetheless, hedonic measures are not without their limitations. In particular, the use of regression techniques implies that hedonic models are only as good as the specifications used to derive them, and often depend on the quality of the data available. If hedonic regressions omit variables that have a significant impact on house prices, this can result in biased estimates of pure price changes.^[6] Analogously, if the relationships between the attributes of houses and their effect on prices are incorrectly specified, for instance through an incorrect functional form, this could also result in biased estimates. For example, Equation (1) could have been formulated with additional second-order terms capturing squared terms of the characteristics vector and allowing for interaction terms between characteristics.

A related question is whether to use an unrestricted hedonic regression, as in Equation (1), where estimates of the implicit price relativities of housing characteristics are allowed to vary between single and repeat sales and over time, or a restricted hedonic regression that assumes the implicit price relativities are the same for both single and repeat sales (γ_t = 0 for all t) and are constant over time (β_t = β, conditional on γ_t = 0 for all t):

In principle, whether Equation (2) is appropriate can be tested by estimating Equation (1) and testing whether the assumptions hold. While these tests provide information about the most appropriate specification, they may be less important in an economic sense if the estimates of pure price changes (the exponential of α_t − α₁) are similar, regardless of whether the unrestricted or restricted specification is chosen.

The results of several empirical studies lend support to the hedonic approach when compared with alternatives. For example, Mark and Goldberg (1984) compare mean, median, hedonic and repeat-sales measures for two Vancouver neighbourhoods and find that hedonic measures (as well as simple measures, such as a median) perform relatively well when compared with their repeat-sales counterparts that appear to underestimate pure prices growth. More recently, Meese and Wallace (1997) use US data and advocate the hedonic approach on the grounds that it is less affected by sample-selection bias (associated with the use of repeat-sales data) and non-constant implicit prices of housing attributes than a repeat-sales measure; similarly, Clapham et al (2004) find that hedonic indices constructed using Swedish data are less prone to revisions than repeat-sales. Comparing hedonic measures with mix-adjusted measures using data from the Netherlands, Francke, Vos and Janssen (2000) suggest that hedonic measures tend to be less sensitive to small market segments. In the Australian context, Rossini et al (1995), Costello (1997) and Flaherty (2004) argue in favour of the hedonic approach when compared with a median on the basis that it is less volatile, and provides some control for changes in the composition and quality of properties sold.

3.2 Repeat-sales Measures

While hedonic measures can, in principle, capture the pure price change in housing, their reliance on a large and high-quality information set regarding house characteristics has led researchers to investigate less data-intensive regression-based methods. Repeat-sales measures, initially proposed by Bailey et al (1963), provide an alternative estimation method based on price changes of houses sold more than once. In particular, if the restricted hedonic model in Equation (2) is differenced with respect to consecutive sales of houses that have sold more than once in the sample period, it follows that:

where for each observation the log resale price is denoted by p_iτ at time t and the previous log sale price is denoted by p_iτ at time τ (t>τ). Assuming that the characteristics of the i^th house do not change between sales (X_it = X_iτ), Equation (3) can be estimated through:

where G_it is a time dummy equal to 1 in the period that the resale occurs, −1 in the period that the previous sale occurs and 0 otherwise, and η_it is again a white noise error term (with an error for each resale, multiple resales are treated as independent observations).^[7]

Advocates of the repeat-sales methodology contend that using a repeat-sales measure more accurately controls for the attributes of houses since it is based on observed appreciation rates of the same house (Bailey et al 1963; Case and Shiller 1987). Repeat-sales measures also require much less data, with information on price, the sales date and the address being the only requirements.

However, repeat-sales measures are estimated on the premise that house characteristics (that is, quality) have not changed over time. Given the non-trivial amount of investment in renovations – often around 2–3 per cent of GDP – and that non-renovated house structures can depreciate with time, it seems unlikely that this will be true. One way to control for this is to use a sub-sample of repeat sales, where quality is thought to be relatively constant. The problem with this approach is that if the sub-sample is too small, the price changes inferred may no longer be indicative of price changes for the full sample of repeat sales. Another control, proposed by Goetzmann and Spiegel (1995), is to use all repeat-sales data and allow for a constant in the repeat-sales regression. In this case, the constant is time invariant and might capture average quality change (across all characteristics), over the average holding period. The suitability of this will depend on whether quality change is correlated with the length of the holding period; a high correlation implies that it will not be suitable as simple repeat-sales methods cannot distinguish between quality and pure price changes temporally. It also depends on the extent to which quality change is not randomly distributed across repeat-sales observations.

Repeat-sales are inefficient in their use of information. The samples used, by construction, only contain information on those houses which have been sold at least twice. If there is a systematic difference between price changes in houses that have been sold only once and those which have been sold more than once, then repeat-sales will provide biased estimates of overall house price changes. Similarly, if there are systematic differences between different types of repeat-sales houses and their rate of turnover (that is, houses sold two, three, four times and so forth), then it is possible for houses with high turnover rates to become over-represented in the sample, again resulting in measurement bias.

Revisions are an issue that can affect both repeat-sales and hedonic measures, since re-estimation with additional data can result in changes in the coefficients estimated and thus the price indices inferred. There have been few empirical studies on this issue to date, though Clapham et al (2004) (Sweden) have found evidence to suggest hedonic indices are relatively more stable than repeat-sales indices.

There is a considerable body of literature advocating repeat-sales measures. Further to the main contributions by Bailey et al (1963), Case and Shiller (1987) and the intercept modification proposed by Goetzmann and Spiegel (1995), a number of alternative repeat-sales estimators have been proposed including arithmetic, geometric and hedonic-repeated measures (Shiller 1991, 1993), Bayesian and Stein-like estimators (Goetzmann 1992) and distance-weighted estimators (Goetzmann and Spiegel 1997). These papers explore several different estimation strategies and generally find that repeat-sales can provide useful additional information using US sales data in their empirical applications (see also Crone and Voith 1992). Using small samples of Australian data, Rossini et al (1995) and Costello (1997) find that a repeat-sales approach compares favourably with a restricted hedonic approach, and that both approaches outperform a median.

3.3 A Simple Mean or Median

The simplest measures of house prices calculate some measure of central tendency from the distribution of prices for houses sold in a period. Since house price distributions are generally positively skewed (predominantly reflecting the heterogenous nature of housing, the positive skew in income distributions and the zero lower bound on transaction prices), the median is typically used rather than the mean. Further, as no data on housing characteristics are required to calculate a median or mean, a price series can be easily inferred.

The simplicity of a median or mean is mitigated, however, by the fact that these measures make no adjustment for the difficulties previously discussed. In particular, a mean or median transaction price is not necessarily representative of the mean or median price of the dwelling stock. This applies both within a given time period and across time periods, suggesting that changes in the mix of properties sold can bias these measures. In addition, a mean or median makes no allowance for changes in the quality of the housing stock over time.

In view of this, a mean or median measure will be an accurate guide to pure price changes only when there is little change in the composition of houses sold between periods, and when quality change is limited. If there is a correlation between turning points in house price cycles and compositional and quality change, then a median could be especially misleading in periods when the premium on accuracy is highest.

3.4 Mix-adjusted Measures

A simple approach to control for changes in the composition of houses sold between periods, but not quality change, is to use a mix-adjusted measure of house prices.^[8] Such measures control for variations in prices across different types of houses by separating the sample into subgroups according to individual house characteristics such as price, location, size, amenities and so forth. A measure of central tendency, such as a median or mean, is then constructed for each group before being combined to construct the aggregate mix-adjusted index. For example, a geometric mix-adjusted index can be constructed as follows:

where MP_t is the mix-adjusted price at time t, w_i is the weight of group i (for instance, expenditure, turnover or housing-stock weights), P_it is the median house price of group i at time t, and n is the total number of groups. This mix adjustment is a relatively simple method of accounting for differences in house characteristics. The data requirements will depend upon the type of groups used, but are generally less intensive than for hedonic price measures. It is also less susceptible to any specification error associated with regression techniques. However, unlike hedonic measures, mix-adjusted measures take no account of quality changes in the housing stock over time.

The effectiveness of a mix-adjusted measure will depend upon the groups used. Generally, a mix-adjusted measure only controls for compositional change across the dimensions defined by each group. For example, if a mix-adjusted measure separates house sales according to their location, changes in turnover across locations should not have a large effect on measured price changes. However, if there is a change in the mix of property types sold that is unrelated to location, then such a mix-adjusted measure will not account for this. Similarly, mix-adjusted measures do not account for changes in the mix of properties sold within each subgroup defined – that is, changes in the mix of properties sold within the boundaries of each defined location.

Mix-adjusted measures of house prices have been used by numerous statistical offices and government agencies including the UK Department of the Environment (1982), the UK Office of the Deputy Prime Minister, and the ABS. Although discussions of this approach have received less attention in academic literature (being more commonly researched and used by statistical agencies), there is a developing body of work on market segmentation using statistical techniques such as cluster and factor analysis (see, for example, Dale-Johnson 1982, Goodman and Thibodeau 2003 and Thibodeau 2003). In principle, cluster and factor analysis can be used to define housing sub-markets or groups, which can then be used as strata in the construction of a mix-adjusted measure. Concurrent research at the ABS (2005) has focused on this approach.

Footnotes

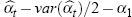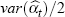More precisely, the exponential of provides the estimated rate of change. In practice, is negligible for large samples (Hill and Melser 2005). [5]

For instance, this can occur where there is a change in an unobserved quality variable over time that leads to a change in prices. [6]

As noted by Shiller (1991), the treatment of multiple resales as independent observations should not be overly problematic because there is no overlap between the holding periods of multiple resales. [7]

Mix-adjusted measures are also referred to as composition-adjusted, fixed-sample or weighted-average measures in the literature. [8]