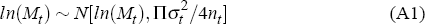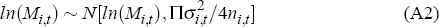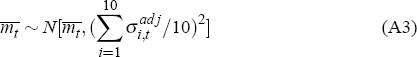RDP 2006-03: Australian House Prices: A Comparison of Hedonic and Repeat-sales Measures Appendix A: Confidence Intervals

For the median confidence interval, I assume that house prices are log-normally distributed. Therefore, the median will be approximately log-normally distributed in large samples as follows (Miller and Miller 1999):

where M_t is the median price of houses sold at time t, σ_t is the standard deviation of log prices at time t and n_t is approximately half the total number of sales at time t (it is the number of sales up to and including the median).^[22]

For the mix-adjusted interval, I first calculate the distribution of the median for each decile in each time period. As above, it is assumed that prices are log-normally distributed and therefore:

Given 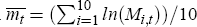ere 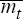is the log of the mix-adjusted measure at time t), and assuming that the sample median of each of the deciles are independently distributed:

where 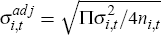. Both the median and mix-adjusted intervals should be treated as indicative, given that the assumptions of log-normality (and independence across decile medians) are not clearly supported by the data.

For our preferred hedonic and repeat-sales measures, the confidence intervals constructed use heteroskedastic-consistent standard errors from their respective OLS regressions.

Footnote

It should be noted that Equation (A1) is also an approximation in the sense that it assumes the log of the median price is sufficiently close to the median of log prices. This is reasonable given the large samples of data used. [22]