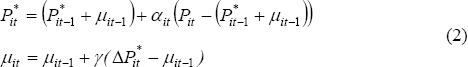RDP 2006-11: Component-smoothed Inflation: Estimating the Persistent Component of Inflation in Real Time 3. An Alternative Measure of Underlying Inflation

3.1 Why Do We Need Another Measure of Underlying Inflation?

An important feature of the world economy over the past few years has been the emergence of China as a significant influence on world production and prices. Its rapid industrialisation has been pushing up commodity prices. At the same time, this industrialisation combined with its relatively cheap labour force has been driving down the price of manufactured goods. More generally, technological innovation has been driving the price of computers and related items down while services, such as education, medical care and child care have seen significant price rises. The net effect of these changes is that the relative prices of individual components of the CPI have been changing significantly and persistently.

This pattern of changing relative prices sits uncomfortably with the assumptions of a number of existing underlying inflation measures (such as the exclusion or reweighted measures discussed in Section 2), which assume that there is a common component to inflation in all series around which there is only idiosyncratic noise. It also means that there is the potential for deviations between headline CPI and various underlying measures to emerge. For example, over the three years to March 2006, the average difference between headline CPI and CPI excluding volatile items in Australia was 0.2 per cent per year,^[3] in the US it was 0.7 per cent over the three years to October 2006. Of course, whether these differences persist over longer periods will depend on the extent to which the rise in the relative price of fuel over this period proves to be permanent or transitory.

Given these considerations, it is worth considering an approach to measuring underlying inflation that is defined as the low- and medium-frequency component of headline inflation. A problem with using the low and medium frequency component of inflation as a conceptual definition for underlying inflation is that it cannot be assessed in real time; it is only with the benefit of hindsight that one can definitively separate transitory shocks from permanent shocks. Notwithstanding this difficulty, the next section considers a measure that uses the information contained in the historical behaviour of the component price series to provide an estimated separation of the permanent and transitory shocks to the CPI in real time.

3.2 Component-smoothed Inflation

The basic method of constructing our component-smoothed inflation measure is to smooth the individual components of the CPI by an amount that is proportional to the volatility in each series. Thus, fruit and vegetable prices are heavily smoothed, because most movements in these series are temporary, while rent is barely smoothed at all, because most movements in this series are highly persistent. This means that only a small fraction of movements in especially volatile prices are allowed to influence the component-smoothed inflation measure in the period they occur because most of these movements are quickly reversed. Nonetheless, if there are persistent changes in these prices, they will contribute to the measure – albeit with a lag.

This approach is, in a sense, a formalisation of a process many economists already undertake informally in interpreting volatile economic series. With a volatile series, economists will often wait for some periods before being convinced that a given movement is going to be sustained. For example, a large movement in average weekly earnings, a particularly volatile series, rarely leads to a change in economists' estimate of the trend rate of wage growth until it is sustained for some periods. Conversely, a large movement in the wage price index, a particularly stable series, leads economists to change their estimate of trend more quickly. The component-smoothed inflation measure does the same thing for individual price series; an increase in the rent series, a particularly persistent series, is reflected almost immediately in our measure, while an increase in petrol prices, a particularly volatile series, needs to be sustained for a number of periods before it is reflected in our measure. This feature has some influence on how movements in our measure are interpreted. We discuss this further when we present our results below.

From this basic methodological approach, we make a number of choices to ensure some desirable properties of the component-smoothed inflation measure. For example, smoothing is applied to the level of the price series to ensure that the measure is unbiased over time. We also choose a smoothing method from the relatively simple class of exponential smoothers to minimise the computation burden of this measure and maximise its transparency.

This approach, smoothing volatile series a lot while leaving persistent series relatively untouched, is analogous to an optimal signal extraction strategy for each series. The Kalman filter, which is often used to identify underlying trends in series, displays just this behaviour.^[4] It reflects the fact that movements in persistent series are informative about the underlying trend – and so one's estimate of the underlying trend should be strongly influenced by new observations – while movements in noisy series are relatively uninformative about the underlying trend – and so one's estimate of the underlying trend should be updated relatively little in light of new observations.

In one sense, this approach can be considered an extension of the idea behind exclusion-based measures. Exclusion-based measures derive from the observation that food and fuel prices are volatile and that movements in these series are more likely to be noise than signal. On this basis, these components – and only these components – are ignored in the calculation of the core measures of inflation. The data, however, are not so black and white. In reality, there are a number of items in the CPI that have similar volatility to food and fuel. For example, some clothing and holiday travel costs are approximately as volatile as food and fuel. Thus, a consistent application of the exclusion principle underlying the core measures could also argue for the exclusion of these categories. However, a choice between complete exclusion or full inclusion is not required. The component-smoothed inflation measure allows a continuum of possible treatments for price series between complete exclusion and full inclusion. No series are completely excluded in the long run, and sustained relative price shifts will be reflected in the component-smoothed inflation measure for even the most volatile components. In another sense, however, component-smoothed inflation differs from other underlying measures because it introduces exponential smoothing, whereas most other measures are calculated entirely from contemporaneous information.

Component-smoothed inflation is calculated using two equations to smooth the price level of each CPI component series. The first equation is just an exponential smoother (with an adjustment to allow for trends in the price level – which is needed because of positive inflation) while the second equation updates the estimate of the trend:

where is the smoothed price level in logs of series i at time t, P_it is the published price level in logs and μ_it is the trend rate of growth of the price level. There are two parameters, α and γ, that control the speed of updating or, equivalently, the amount of smoothing. These parameters are restricted to lie between 0 and 1. Our implementation links α and γ so, in practice, only one parameter needs to be chosen.^[5]

The parameter α determines how quickly changes in a series' price level are reflected in the smoothed series. A high value of α means that changes will be reflected almost immediately, while a low value of α passes through very little of the change. There are a variety of ways to choose α, but, based on our objective to remove transitory volatility, we choose α based on the signal-to-noise ratio of the price series.^[6] Thus, a highly persistent series would have α = 1, and there would be no smoothing, while a series dominated by temporary shocks would have a small value for α and a high degree of smoothing. This has the effect of smoothing transitory shocks while leaving persistent movements relatively unaffected. In a similar manner, the parameter γ controls the speed with which the estimate of trend is updated. If γ = 0 there is no updating and the trend remains constant throughout the sample.

The basic formula for α is:

where Q is a parameter that controls the smoothness of the component-smoothed inflation measure and R_it is the variance of the noise in the raw price series. R_it is calibrated for each series as the variance of deviations of the observed price series P_it from its Henderson trend based on data up to time t. A series with little noise will have small deviations from its Henderson trend, so that R_it will be small and, consequently, α_it will be close to unity. A series containing a lot of noise will deviate substantially from its Henderson trend, and have a low value for α_it . In practice, the values of R_it do not appear to matter as much as the ranking between the CPI series that they provide.

While Q needs to be in the same units as R, the precise value for Q is somewhat arbitrary and can be thought of as the ‘target’ for how smooth the researcher would like the underlying measure to be. A higher value for Q will lead to a more volatile underlying series while a lower value will have the opposite effect. At the limits, if Q = 0 all the α parameters would be zero and the resulting series would be a constant, while α approaches 1 for large Q and, in the limit, the resulting series would be the headline CPI. Our particular choice is guided by the desire to capture enough medium-term movements to allow policy-relevant inference about inflationary pressures to be made. We discuss the exact values chosen in Sections 4.1 and 4.2.

When comparing the results based on Equation (3) to those of the Kalman filter we find that highly volatile series are smoothed too much and so the lag before sustained price changes were reflected in the index was judged to be too long. Thus, we adopt one small modification to the formula for α to limit the extent of smoothing. We modify Equation (3) and set α_it as:

where β sets a lower bound for a_it, which ensures that even very volatile series still make some contribution to the final index. Because only data up to time t are used to calculate R_it, the smoothing process can be performed in real time.

In keeping with our approximation to the Kalman filter we choose 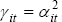. This specification updates the estimate of the trend quickly for series with little noise, and more slowly for series that contain more noise – something that also has obvious intuitive appeal.

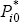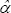As the smoothing process is recursive, the initial values need to be set. We set equal to P_i0, μ_i0 equal to the growth rate of the CPI in the period before the algorithm is started and α_it = , a constant, for an initial three-year period. After three years the estimates for α_it are updated and the first three years of data are used to calculate the first value of α_it, and the sample used to calculate α_it is lengthened recursively with the release of each new observation.^[7]

3.3 Features of Component-smoothed Inflation

The component-smoothed inflation measure can be thought of as an implementation of the idea expressed in Blinder (1997), whereby underlying inflation is the persistent component of inflation. However, rather than down-weighting volatile series, our measure maintains the CPI weights and removes the noise from the series through exponential smoothing. While the maintenance of CPI weighting has obvious intuitive attractions, an additional advantage of maintaining expenditure weights is that it helps to ensure that the measure is unbiased in the long run with respect to headline inflation. As discussed above, sustained relative price shifts have been a particular feature of CPIs around the world over recent years. Our measure is robust in the long run to persistent relative price changes of this sort.

While smoothing each individual CPI component requires more calculation than just smoothing aggregate inflation, a significant advantage is that identification and removal of transitory shocks is much easier at the disaggregated level. To see this most clearly consider a trivial example where the CPI is made up of two series, where one is very noisy and contains no long-term trend (white noise for example), while the other is highly persistent (say, a random walk). At the aggregate level it would not be possible to separate the temporary from the persistent shocks in real time. At the component level, separating the temporary shocks from the persistent shocks is trivial. While the distinction is not quite so easy in the real world, there are still series that are historically highly persistent, such as rent, while others, such as fruit, have historically been characterised by frequent temporary price shocks.

Another feature of the measure is that some lag relative to the headline CPI can arise in circumstances where history has shown that the movements are quickly reversed. If a historically volatile item experiences a persistent change in price, the measure will lag, though to some degree recognition lags are probably inevitable with any measure in these circumstances. There is little problem with temporary shocks to persistent series as they only serve to add a little extra volatility to the series.

Another property of the component-smoothed inflation measure is that a number of existing measures of inflation can be thought of as special cases. For example, headline inflation is equivalent to setting all α_i = 1 and the exclusion measures are equivalent to setting α_i = 0 for the excluded components and α_i =1 for the rest. This relationship will be discussed further below when this paper's measure is compared with existing measures of inflation.

Papers by Roger (1998) and Wynne (1999) have proposed a number of properties for underlying inflation measures which they see as desirable. The component-smoothed inflation measure is designed, wherever possible, to have these properties. Thus, it is timely as it can be calculated in real time, it is unbiased by construction, and we have also endeavoured to make it easy for the public to understand and verify by choosing to use exponential smoothing and opting towards simpler formulations wherever possible.^[8] As argued for by Wynne, the component-smoothed inflation measure is non-revisionary and, as is shown below, because it focuses on the persistent component of inflation, has some predictive power for future inflation.

Finally, while we calculate the component-smoothed inflation measure based on headline inflation in this paper, it would be a simple matter to base the construction on any other inflation measure. This would result in a measure that is unbiased with respect to that measure of inflation, but smoother. This would seem to be of most relevance in countries where some other measure of inflation is the legislated, or otherwise chosen, target of policy.

A more detailed evaluation of the performance of the component-smoothed inflation measure is contained in the next section which presents the measure for Australia and the US and compares these results with commonly used measures of underlying inflation in each country.

Footnotes

March 2006 is chosen to avoid the ‘banana effect’ dominating the comparison. Over the three years to September 2006 the average difference is 0.81 per cent per year. [3]

The exponential smoother can be viewed as an approximation to the theoretically more appropriate Kalman filter (see Hamilton 1994 for details of the Kalman filter). In practice, the Kalman filter gain quickly converges to a constant in the case of the data we use in this paper and, as such, the use of a time-invariant gain is not significantly inferior to the time-varying gain of the Kalman filter. [4]

This method is sometimes called ‘double exponential smoothing’. The double refers to the second equation which ensures that the smoother follows trends whereas ‘exponential smoothing’ cannot be guaranteed to be unbiased with respect to the original series. [5]

This is also consistent with our method's interpretation as an approximation to the Kalman filter. A superficially appealing alternative to using the signal-to-noise ratio for a series to calibrate α would be to use the autoregressive parameter for the price series. A problem with this approach, however, is that it is not robust to medium-term shifts in the rate of inflation for a series. For example, many Australian inflation series, including ones that are highly volatile, have a high autoregressive parameter when calculated over any period incorporating the decline in inflation in the early 1990s. Nonetheless, we consider this alternative in Section 4.3 when we test the robustness of our measure. [6]

Occasionally new series are added to the CPI. When this occurs, we set the α parameter for the new series to that of the most similar series already in the index for the first three years of its inclusion. For example, in Australia the education fees price series was replaced with three series (primary, secondary and tertiary education) with the introduction of the 14^th series CPI. For the first three years we set the α for these three series based on the α for the older aggregate education series. [7]

Exponential smoothing and the other steps required to calculate component-smoothed inflation can all be implemented in a spreadsheet while other methods may require more specialised software. [8]