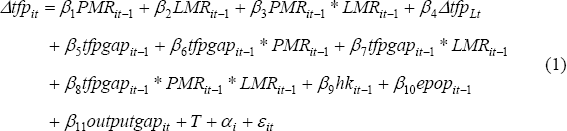RDP 2007-04: Productivity Growth: The Effect of Market Regulations 3. Data and Method
June 2007
- Download the Paper 471KB
This paper uses fixed-effects panel data regressions with growth in TFP as the dependent variable. We examine the effects of product and labour market regulation on TFP growth in 18 OECD countries from 1974 to 2003.[8] Appendix A provides detailed descriptions of our data and its sources while Table 1 summarises the key data.
| TFP growth(a) | Product market regulation(b) | TFP gap(c) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1983 | 1993 | 2003 | 1975 | 1983 | 1993 | 2003 | 1973 | 1983 | 1993 | |||
| Australia | 0.41 | 1.05 | 1.80 | 4.0 | 4.0 | 3.2 | 1.5 | −31.9 | −30.1 | −32.3 | ||
| Belgium | 1.84 | 1.15 | 0.85 | 5.5 | 5.5 | 4.6 | 2.1 | −34.2 | −17.5 | −21.1 | ||
| Canada | −0.25 | 0.90 | 1.45 | 4.3 | 4.3 | 2.5 | 1.9 | −3.1 | −7.6 | −12.9 | ||
| Denmark | 0.80 | 0.69 | 0.92 | 5.5 | 5.5 | 4.2 | 1.6 | −39.5 | −33.0 | −40.1 | ||
| Finland | 2.05 | 1.85 | 2.97 | 5.5 | 5.4 | 4.2 | 2.4 | −63.9 | −53.6 | −51.4 | ||
| France | 0.73 | 0.79 | 0.92 | 6.0 | 6.0 | 4.9 | 3.0 | −4.2 | −0.8 | −5.9 | ||
| Germany | 1.22 | 1.04 | 1.26 | 5.2 | 5.1 | 4.2 | 1.7 | −28.6 | −19.5 | −23.5 | ||
| Ireland | 3.59 | 3.91 | 4.44 | 5.7 | 5.7 | 4.7 | 3.2 | −80.9 | −51.1 | −25.5 | ||
| Italy | 1.45 | 1.53 | 0.67 | 5.8 | 5.8 | 5.3 | 2.6 | −24.8 | −17.1 | −19.0 | ||
| Japan | 1.11 | 1.68 | 0.41 | 5.1 | 5.1 | 3.3 | 2.2 | −38.9 | −38.0 | −35.4 | ||
| Netherlands | 1.65 | 1.51 | 0.67 | 5.6 | 5.6 | 4.2 | 1.6 | −22.2 | −9.2 | −8.2 | ||
| NZ | – | – | 1.11 | 4.9 | 4.5 | 3.0 | 2.1 | – | – | −36.1 | ||
| Norway | 2.41 | 2.01 | 2.28 | 5.5 | 5.5 | 3.6 | 2.3 | −22.0 | −6.8 | 0.0 | ||
| Spain | 1.38 | 1.12 | 0.41 | 5.1 | 5.0 | 4.5 | 2.0 | −24.9 | −15.1 | −16.8 | ||
| Sweden | 0.56 | 0.97 | 1.92 | 4.5 | 4.5 | 3.3 | 1.9 | −33.6 | −31.9 | −37.1 | ||
| Switzerland | – | – | 0.58 | 4.1 | 4.2 | 4.2 | 2.8 | – | – | −42.3 | ||
| UK | 1.54 | 1.22 | 1.28 | 4.8 | 4.5 | 2.2 | 1.0 | −26.4 | −14.6 | −17.2 | ||
| US | 0.28 | 1.23 | 1.59 | 3.7 | 2.7 | 2.2 | 1.4 | 0.0 | 0.0 | −1.5 | ||
| Average | 1.30 | 1.41 | 1.42 | 5.0 | 4.9 | 3.8 | 2.1 | −28.1 | −21.6 | −23.7 | ||
| Days lost to labour disputes(d) | Employment protection legislation(e) | Union density(f) | ||||||||||
| 1973 | 1983 | 1993 | 2003 | 1973 | 1983 | 1993 | 1973 | 1983 | 1993 | |||
| Australia | 450.8 | 413.0 | 137.3 | 39.0 | 0.0 | 0.0 | 1.1 | 50.2 | 47.2 | 37.5 | ||
| Belgium | 216.9 | 56.8 | 27.4 | 21.0 | 3.0 | 3.0 | 2.6 | 47.6 | 51.9 | 55.0 | ||
| Canada | 570.9 | 563.4 | 159.7 | 151.0 | – | 0.6 | 0.6 | 34.6 | 36.6 | 32.8 | ||
| Denmark | 550.4 | 114.4 | 31.6 | 37.7 | 0.0 | 0.0 | 1.9 | 62.2 | 80.8 | 77.3 | ||
| Finland | 888.8 | 223.7 | 78.9 | 28.5 | – | 2.2 | 2.2 | 61.4 | 68.8 | 78.8 | ||
| France | 189.7 | 87.5 | 37.6 | 73.8 | 2.7 | 2.7 | 2.9 | 22.1 | 16.0 | 10.1 | ||
| Germany | 67.4 | 1.5 | 16.6 | 4.3 | 3.6 | 3.6 | 3.2 | 32.4 | 35.0 | 31.8 | ||
| Ireland | 213.4 | 341.0 | 94.7 | 32.8 | 0.8 | 1.0 | 1.0 | 53.3 | 57.2 | 50.0 | ||
| Italy | 1001.9 | 699.3 | 146.5 | 121.0 | 0.0 | 4.2 | 3.8 | 43.3 | 45.5 | 39.2 | ||
| Japan | 101.9 | 9.4 | 2.3 | 0.3 | 2.6 | 2.6 | 2.6 | 33.5 | 29.8 | 24.3 | ||
| Netherlands | 45.9 | 20.2 | 11.0 | 21.5 | 3.1 | 3.1 | 2.8 | 36.2 | 31.3 | 25.9 | ||
| NZ | 140.5 | 236.4 | 51.7 | 21.8 | 0.0 | 1.0 | 1.0 | 56.3 | 64.5 | 34.5 | ||
| Norway | 6.6 | 54.1 | 66.8 | 22.2 | 1.6 | 3.1 | 3.0 | 53.2 | 58.1 | 58.0 | ||
| Spain | 67.0 | 359.2 | 338.5 | 157.4 | 0.0 | 3.7 | 3.5 | – | 8.9 | 18.0 | ||
| Sweden | 74.4 | 19.6 | 19.8 | 50.4 | 0.0 | 3.4 | 2.9 | 72.5 | 79.6 | 83.9 | ||
| Switzerland | 1.0 | 0.5 | 0.1 | 3.8 | 1.3 | 1.3 | 1.3 | 27.8 | 29.6 | 22.9 | ||
| UK | 609.2 | 186.3 | 25.2 | 28.0 | 0.4 | 0.5 | 0.5 | 45.5 | 48.0 | 36.1 | ||
| US | 419.3 | 144.2 | 35.2 | 14.3 | 0.0 | 0.0 | 0.2 | 26.3 | 21.7 | 16.9 | ||
| Average | 312.0 | 196.1 | 71.2 | 46.0 | 1.2 | 2.0 | 2.1 | 44.7 | 45.0 | 40.7 | ||
|
Notes: (a) Ten-year average of annual growth ending in the year shown.
Average for Finland and Norway begins in 1976. Source: See Appendix A |
||||||||||||
We run the regression with observations over three 10-year blocks. While the data are annual, estimating the regression over 10-year periods lets us better capture any relationship between TFP growth, which is quite volatile from one year to the next, and changes in the structure of product and labour markets, which are likely to have a delayed and more gradual impact on TFP growth. This is also one way to attempt to control for any influence of the business cycle on measured TFP growth (discussed further below).
The dependent variable in our regressions is growth in TFP in the business sector. We calculate TFP from OECD data converted to US dollars using purchasing power parity exchange rates to increase cross-country comparability. Restricting our analysis to the business sector avoids the problems of measuring output and productivity in the government sector, and using an hours-based measure of labour inputs avoids the well-known problems with time series comparisons of heads-based productivity estimates. An important difference between our measure of TFP and some others is our measure of labour's share of income (LSI): we include an approximation of labour's share of gross mixed income (GMI) in our estimate of LSI.[9]
The general specification we use for our regression analysis is a modified version of that in Griffith, Redding and Van Reenan (2000) and is based on a ‘catch-up’ theory of TFP growth. This theory suggests that, other things equal, countries further from the technological frontier will experience more rapid TFP growth, given their opportunities to adopt more advanced productive practices of those countries at the frontier. Following Griffith et al, we assume that TFP growth is an auto-regressive distributed lag (1,1) process in which the level of TFP in each country is co-integrated with that in the technological leader. This specification allows for the possibility that TFP growth rates may converge in the long run, but that differences in the level of TFP can persist. If we also assume long-run homogeneity, TFP growth in a given country at time t will be a function of TFP growth in the technological leader and the technological ‘gap’ for each country, which is the difference between the logged levels of TFP in country i and the technological leader (see Equation (1) below).
To test the effects of regulation on TFP growth we add measures of product and labour market regulation on their own, in combination, and (following Nicoletti and Scarpetta 2003) in combination with the technology gap.[10] The products of regulatory terms with the technology gap allow for the possibility that the effects of labour and product market regulations on productivity may depend on a country's distance from the productive frontier.
Our measure of product market regulation is an OECD index, which provides an internationally comparable measure of the degree to which government policies inhibit competition. This index is based on a number of sub-indices covering regulations related to barriers to entry (including legal and administrative barriers to entrepreneurship), public ownership, market structure, vertical integration and price controls in seven non-manufacturing industries (for more details see Appendix A and Conway and Nicoletti 2006). The index ranges from most restrictive (6) to least restrictive (0), and is an annual time series available from 1975–2003. We can think of this index as a ‘direct’ measure of a country's economic structure, in the sense that it is directly related to a country's economic regime, rather than being a consequence of that structure.
Like most proxies, direct measures of product market competition such as these have both advantages and disadvantages. A significant advantage of direct measures of the regulatory structure is that (provided regulators do not deregulate opportunistically) they are more exogenous to the macroeconomic variables under investigation than traditional proxies such as firms' mark-ups. Two potential disadvantages are that proxies based on statutes cannot adjust for the way that the statutes are enforced in practice, and that the regulations might be a poor proxy for competition because, even if enforced, they do not actually affect competition. The OECD indices attempt to adjust for enforcement by including some data on actual market structures. Also, the few direct tests of the OECD indices conducted to date suggest that they are correlated with traditional indicators of competition such as firm entry rates and sectoral mark-ups (Conway and Nicoletti 2006).
Our preferred measure of labour market regulation (LMR) is a proxy based on the number of days lost in labour disputes, but we test the sensitivity of our results to alternative measures in Section 5. While the annual data are quite volatile, a three-year moving average shows a trend decline across most countries, and this trend appears to be consistent with the variation in the extent of labour market reforms across countries.[11] Because the approach to industrial relations reform has been quite different across countries, an outcome-based measure such as this may be better than a direct measure. For example, Wooden and Sloan (1998) show that while Australia and the UK adopted different approaches to labour market reform, they have resulted in very similar labour market outcomes.
Both the PMR and LMR variables enter our regressions in levels rather than changes. With this specification, the literal interpretation of a significant negative relationship between a regulatory variable and TFP growth is that deregulating the relevant market causes a permanent increase in the growth rate of TFP. Although we do find such significant econometric relationships, we would caution against this literal interpretation. This is because it may be difficult to distinguish between lower levels of regulation leading to higher levels or higher growth rates of TFP over our sample period.
To avoid attributing changes in the quality of labour to changes in TFP growth, we include two controls for changes in labour quality in our regressions. The first is average years of schooling, a proxy for human capital. Clearly this is imperfect as it measures a process (education) rather than an outcome (human capital formation) and does not capture post-school human capital formation. However, Bassanini, Scarpetta and Hemmings (2001) note that the specific series used in their paper represents an improvement upon those generally used in the literature.[12]
The second control is an employment-to-population ratio. This should capture variation in the quality of labour inputs arising from the employment of more or less productive employees over time. Various versions of this measure have been found to be significant in related studies.[13] The choice of both the denominator and numerator are potentially important here. The choice of the denominator (total population, population aged 15 and older or population aged 15–64) affects the extent to which changes in an employment-to-population ratio reflect changes in the age structure of the population (which are not necessarily related to labour productivity). We choose the denominator (population aged 15–64) that is likely to be least susceptible to demographic changes, given our sample period. For the numerator we choose business sector rather than total employment, although there are potential problems with either measure. Total employment would fall if public sector employment fell with unchanged business sector employment, which we would expect to have only a tenuous relationship with the marginal productivity of employees in the business sector, our sector of interest. Conversely, we might expect the marginal productivity of new entrants into private sector employment to differ depending on whether they came from outside the labour force, unemployment, or the public sector, but our measure will only register an increase in the employment rate regardless of the origin of the entrants.
Measured TFP growth may be influenced by the state of the business cycle, and business cycles are not perfectly synchronised across countries. It follows that international comparisons of productivity growth may be distorted unless one controls for the business cycle in each country. This can be done by including an indicator of the cycle as an independent variable. Alternatively, the dependent variable could be smoothed to remove its cyclical component. Skoczylas and Tissot's (2005) analysis of cross-country labour and multifactor productivity compares these methods. While they favour the former, the authors note that for most countries in their sample the results of each method are broadly similar. We make use of both approaches in this paper. When using data over 5- or 10-year blocks, much of the effect of the cycle is controlled for indirectly. We also include an output gap as an indicator of the cycle in our regressions. Our gap is the difference between the natural logarithms of actual and trend business sector output, where trend is constructed with an HP filter. The standard endpoint problem is partially mitigated by including three years of OECD forecasts for business sector output when smoothing these series.[14]
In summary, we estimate regressions based on the following general formulation:
where: Δtfpit and ΔtfpLt are average annual growth in TFP for country i and the leading country L over the time period, t, in question; PMRit−1 is the lagged level of the product market regulations index; LMRit−1 is the lagged level of working days lost to labour disputes (smoothed by taking averages over three-year periods); tfpgapit−1 is the level of the gap between TFP in country i and the leading country; hkit−1 is the lagged level of average years of schooling; epopit−1 is the lagged level of the ratio of employment to the working-age population; outputgapit is the average annual value of the output gap over the period t; and T is a time trend. The time periods are the three 10-year blocks ending in 1983, 1993 and 2003. The regulation variables, TFP gap, human capital and employment-to-population ratio are all measured on a period-ended basis, that is, the year just prior to the start of the 10-year block t; the exception to this is for the first 10-year period for which the PMR index is only available for 1975.
Footnotes
As discussed below, we exclude observations for Japan and the Netherlands in the 1990s from most of the regression analysis. [8]
Specifically, we assume that all self-employed are paid average wages. The conceptually correct method for calculating LSI is to sum compensation of employees (CoE), labour's share of GMI and net taxes on labour. Of course, labour's share of GMI is positive, and net taxes on labour are also likely to be positive (and relatively small). Hence the standard technique of approximating the numerator of LSI solely with CoE yields LSI estimates that are biased downwards. As LSI is the weight on labour inputs in calculations of TFP, bias in the level will affect estimates of TFP growth. [9]
Griffith et al (2000) use an endogenous growth framework to derive a model of productivity growth incorporating R&D. Scarpetta and Tressel (2002) and Nicoletti and Scarpetta (2003) adapt this specification, replacing R&D in the original equation with PMR. While Griffith and Harrison (2004) criticise this replacement as being ad hoc, Scarpetta and Tressel and Nicoletti and Scarpetta do suggest mechanisms through which product market competition can affect the adoption of new technologies. [10]
It is possible that there is a mechanical relationship between the days lost to labour disputes in one year and TFP growth in the next. Whether or not such a relationship exists depends on: (i) how the labour input of striking employees is measured in each country in our sample; and (if measured hours worked do fall as a result of industrial action) (ii) the extent to which this decrease in labour inputs results in a fall in output, TFP, or some combination of the two. Even if such a mechanical relationship does exist, its effect will be negligible as our dependent variable is average TFP growth over 10- or 5-year periods. [11]
For an examination of the importance of human capital in closing Australia's labour productivity gap with the US, see Dolman, Parham and Zheng (2007). [12]
For example, Belorgey, Lecat and Maury (2004) find a negative association between labour productivity and the change in the employment rate, where the denominator of the latter is the total population. Gust and Marquez (2004) find a negative association between business sector labour productivity growth and the change in the ratio of total employment to the population aged 15 and older. [13]
We also estimated regressions below using output gaps from the OECD's Economic Outlook No 78 database. Their results were very similar. [14]