RDP 2007-04: Productivity Growth: The Effect of Market Regulations 4. Results
June 2007
- Download the Paper 471KB
The first point to note is that regressions based on the full sample (results not reported) show that residuals for Japan and the Netherlands in the 10-year period ending in 2003 stand out as being particularly large.[15] This is because these countries experienced sizeable declines in PMR from 1983 to 1993, but also experienced among the largest declines in average TFP growth from the 10 years ending in 1993 to the 10 years ending in 2003. In what follows we exclude observations for the Japan and the Netherlands in the 1990s. The exclusion of outlying observations is fairly common in the literature, in part reflecting problems with errors in variables and omitted variables that may be especially relevant to some observations (see, for example, Nicoletti and Scarpetta 2003). For Japan, the after-effects of the financial bubble are likely to have played an important role. For the Netherlands, wage moderation enabled a very large rise in participation through the 1990s (without a commensurate increase in labour market flexibility), which was associated with a sharp decline in labour and total factor productivity (for a discussion of the Dutch case, see Naastepad and Kleinknecht 2002 and Bell 2004).
The key results of estimating a number of variants of Equation (1) using OLS appear in Table 2. Model 1 is a basic regression with only the PMR and LMR measures (and their interactive term) included. The coefficients on the LMR and interactive terms are significant by themselves. The coefficient on PMR is not – its p-value is 0.108, but excluding it from the model leads to a drop in the fit of the model of around 20 per cent. The PMR variable is significant in the absence of the LMR and interactive terms (results not shown), and its coefficient is of a similar order of magnitude as per Model 1.
| Variables | Lag | Model | |||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4(a) | ||
| PMR | t−1 | −0.22 | 0.12 | −0.23** | |
| LMR | t−1 | −0.009*** | −0.016*** | −0.010*** | −0.008*** |
| PMR*LMR | t−1 | 0.0016*** | 0.0030*** | 0.0019*** | 0.0016*** |
| Human capital | t−1 | 0.068 | |||
| Employment/population | t−1 | −0.070 | |||
| TFP growth leader | t | 0.042 | |||
| TFP gap | t−1 | −0.087** | −0.085*** | ||
| TFP gap*PMR | t−1 | 0.015* | 0.015*** | ||
| TFP gap*LMR | t−1 | −0.0003 | |||
| TFP gap*PMR*LMR | t−1 | 6.4xl0~5 | |||
| Output gap | t | −0.21*** | |||
| Number of observations | 48 | 48 | 48 | 82 | |
| R2 within(b) | 0.34 | 0.57 | 0.49 | 0.30 | |
| p-value for rejecting | 0.025 | 0.000 | 0.000 | 0.000 | |
| F-test of overall significance | |||||
| Notes: ***, ** and * indicate that coefficients are significant at the 1,
5 and 10 per cent significance levels, respectively, using robust standard
errors. All models exclude observations from 1994 to 2003 for Japan and
the Netherlands. PMR – index from 0 (least) to 6 (most) restrictive.
LMR – days lost to labour disputes per 1000 employees. (a) Based onfive 5-year blocks, ending in 1983, 1988, 1993, 1998 and 2003. (b) The R2 within does not take account of the explanatory power from the constant. |
|||||
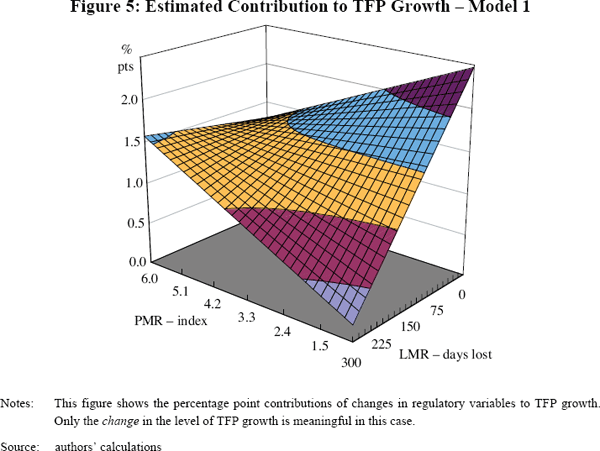
Because of the interactive term, the interpretation of the marginal contributions of reforms in labour and product markets depends on the level of the other regulatory variable. This can be seen in Figure 5, where changes in the vertical height of the surface show the estimated changes in TFP growth for given changes in LMR and PMR. From the initial to the most recent observations of PMR and LMR included in our panel, most countries moved from points near the front and left of the surface, to points towards the right and rear of the surface. Within much of the region of reforms actually observed, the shape of the surface shows that deregulation in labour and product markets had large effects when undertaken in combination.[16]
Model 2 is the more comprehensive specification, with human capital, the employment-to-population ratio, the TFP gap and related interactive terms with the regulatory variables all included.[17] The TFP gap by itself is significant and enters with a negative coefficient. As all TFP gaps are negative or zero, this implies that the further a country is behind the lead country, the faster will be its average TFP growth over the next decade. While PMR is not significant on its own, its interactions with both LMR and the TFP gap variables are both significant. The coefficient on the interactive term between PMR and TFP gaps is positive, implying that the technology gap tends to have closed more quickly when product market regulations were less restrictive. Because of the interactive terms, the interpretation of the marginal contributions of reforms in labour and product markets depends on the level of the other regulatory variable, and the level of the technology gap. To interpret these interactions, we remove the insignificant variables from Model 2 to obtain the parsimonious Model 3.
The estimated contribution to TFP growth of changes in the regulatory environment can be illustrated with a surface similar to that of Figure 5 for each of three different TFP gaps: large; intermediate; and small. These surfaces are shown in Figure 6, where changes in the height of the surfaces show the estimated changes in TFP growth for given changes in LMR and PMR, conditional on the TFP gap.
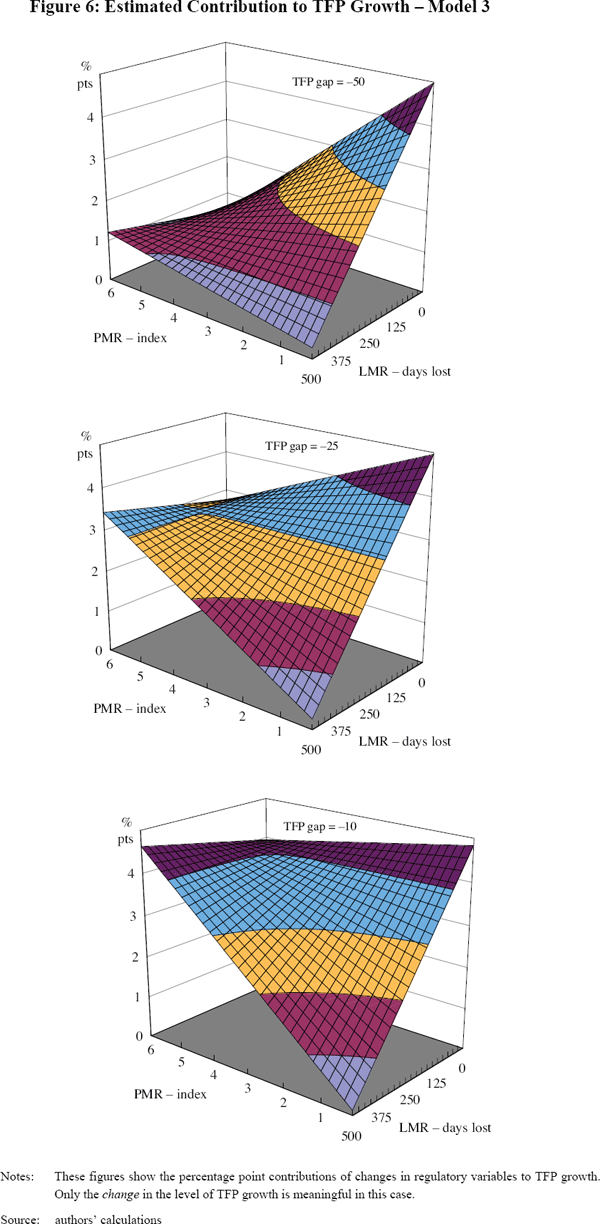
For all three TFP gaps, the contribution of labour market deregulation is positive so long as the product market is not too heavily regulated (a PMR index of less than about 5.3), and the contribution is larger at lower levels of product market regulation. The contribution of product market deregulation depends on the levels of both LMR and the technology gap. For each gap, the estimated marginal contribution of product market deregulation is negative for higher levels of labour market regulation; the level of LMR needed to make a marginal change in PMR positive falls as the technology gap closes. For moderate to low levels of labour market regulation, product market reforms are estimated to make a positive contribution to TFP growth. This contribution is larger the lower is labour market regulation, and the larger is the TFP gap.
Model 1 is fairly robust to the inclusion of an output gap or the exclusion of each individual country from the sample, although the coefficient on PMR is not as stable as the others. While the coefficients on LMR and the interactive term are quite robust, adding a time trend or time dummies roughly halves the coefficient on PMR. The same tests[18] for Model 2 reveal that the coefficients on PMR, human capital and TFP growth in the leading country are generally rather unstable. This is probably driven in part by the high correlation between some of the variables in the model (in particular between PMR and human capital) which makes their coefficient estimates sensitive to small changes in the sample. The parsimonious Model 3 is robust to the inclusion of an output gap, the inclusion of time trends or time dummies, and to the exclusion of individual countries from the sample. The coefficient on the output gap was not itself significant in any of the models.
Our specification of Equation (1) suggests two further robustness checks. Strictly speaking, when Equation (1) includes the technology gap terms it is only relevant for countries that are not the technological leader. We therefore follow Griffith et al (2000) and re-estimate Models 2 and 3 excluding Norway and the US (results not shown). Model 3 is completely robust to their exclusion and Model 2 is generally robust. If our sample were larger, we would include one further check: re-estimating Models 2 and 3 with instrumental variables (IV) to confirm that any downward bias arising from the inclusion of the technology gap in the fixed-effects specification is small as theory suggests. Unfortunately, given the instruments available to us, IV reduces our sample size so much as to make estimation unreliable.[19]
We also examined results based on using data in 5-year blocks (Model 4 in Table 2). This has the advantage of more degrees of freedom by greater use of the time dimension, but at the expense of a potential increase in measurement error. To account for the impact of the business cycle on measured TFP growth we included the output gap in regressions. The main difference between these and the 10-year block regressions is that the TFP gap and its interactive terms were no longer significant. The results for the parsimonious Model 4 is very much like that of Model 1 (based on 10-year blocks), though with PMR now significant in its own right. This was not the case in the presence of time trends or time dummies, though the time trend was not significant in the presence of the PMR variable and the inclusion of the trend added only marginally to the explanatory power of the model.
Footnotes
The residual for Canada in the 1970s is also large, but exclusion of this observation makes no substantial difference to the following results. [15]
The estimated marginal effect of labour market deregulation on TFP growth is positive for values of PMR below 5.4. Between 1975 and 1993, average PMR fell from 5.0 to 3.8, so the estimated marginal contribution of changes in LMR has been positive for most countries over the sample period. The estimated marginal effect of product market deregulation is positive for values of LMR below 138 days lost per 1000 employees. Over 1973–1993, average working days lost fell from 312 to 71, so that the marginal effect of product market deregulation is estimated to have become positive for most countries during the sample period. [16]
Although the time series was too short for inclusion in the 10-year regression, we estimated the regression based on 5-year blocks (see below) with an indicator of R&D expenditure, which was insignificant (results not shown). Econometric research into the effects of R&D expenditure on TFP growth (for example, Scarpetta and Tressel 2004) suggests that the effects depend on the type of technology in a given industry and hence may be difficult to detect in an aggregate analysis. [17]
With the exception of adding time dummies or trends. Because the average TFP growth of the leader is constant across countries, it can be expressed as a function of the time dummies, giving a near-perfect dependence between a subset of the explanatory variables. Also, the correlation between the time trend and average TFP growth of the leader is extremely high, so including a time trend risks generating spurious results and introducing yet more collinearity into Model 2. [18]
Nickell (1981) showed that a fixed-effects model with a lagged dependent variable generates estimates that are biased downwards when the number of time periods (T) is small. Judson and Owen (1999) showed that, for the kinds of panels commonly found in macroeconomics (relatively more time periods and fewer cross-sections than in the typical microeconomic panel), the size of this bias can be between 3 and 20 per cent of the true size of the coefficient even when T is as big as 30. While it would still be desirable to check that the bias is small in our case, Equation (1) is a non-standard example of this type of bias problem because, rather than being a lagged dependent variable, the technology gap that appears on the RHS of Equation (1) is related to the lagged dependent variable by construction. This means that it is not feasible to use existing methods such as bias correction (Bruno 2005) or the generalised method of moments to generate unbiased estimates for Equation (1). Hence IV is the only technique open to us, but, given the available instruments, it reduces our sample size so much as to make estimation unreliable. Fortunately it is likely that the differences between our model and a standard lagged dependent variable fixed-effect model make any potential bias even smaller. For example, like Scarpetta and Tressel (2004) and Griffith et al (2000), we use different indices of TFP on the LHS and RHS of Equation (1); the index on the RHS is a superlative index that permits comparison of the levels of TFP across countries. Although the underlying data are the same, the indices are constructed differently so any correlations and bias would probably be smaller than would be the case in a more standard regression with a lagged dependent variable, other things equal. [19]