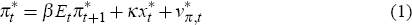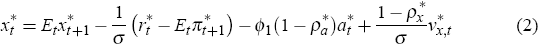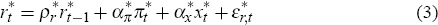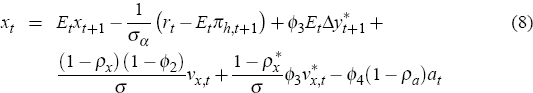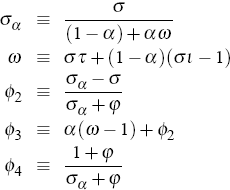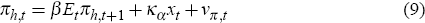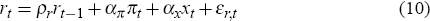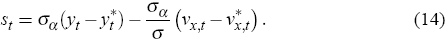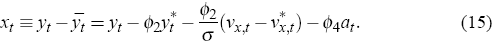RDP 2007-06: The Butterfly Effect of Small Open Economies 2. The Model
June 2007
- Download the Paper 247KB
The model is a version of Galí and Monacelli's (2005) fully micro-founded, stochastic, dynamic, general equilibrium, sticky-price small open economy model. Some broad features of the model are: all output is tradable; prices are sticky as in Calvo (1983); there is full exchange rate pass-through; and there are complete securities markets.
We add foreign and domestic aggregate demand and supply shocks and keep the large economy in its structural form.[5] Instead of working through the details of the derivation, which are in Galí and Monacelli, we present the key log-linear aggregate relations.
2.1 The Large Economy
Variables with a star superscript correspond to the large economy, which can be described with a standard set of new Keynesian closed economy equations.[6]
Firms operate under monopolistic competition in the goods market and Calvo-price stickiness. Factor markets are competitive and goods are produced with a constant returns-to-scale technology. One can show that the Phillips curve in the large economy takes the form
where: 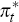 stands for the foreign inflation rate;
stands for the foreign inflation rate; 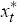 is the foreign output gap;
is the foreign output gap; 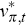 is a foreign cost-push
shock; the parameter κ is strictly positive and captures the
degree of price rigidities; the household's discount factor, β,
lies between zero and one; and Et denotes expectations
conditional on information at t.
is a foreign cost-push
shock; the parameter κ is strictly positive and captures the
degree of price rigidities; the household's discount factor, β,
lies between zero and one; and Et denotes expectations
conditional on information at t.
The aggregate demand schedule (IS-curve) implies that the current level of the foreign
output gap, 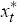 ,
depends on its expected future level, the ex-ante short-term real
interest rate, foreign total factor productivity,
,
depends on its expected future level, the ex-ante short-term real
interest rate, foreign total factor productivity, 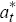 , and a foreign aggregate
demand disturbance,
, and a foreign aggregate
demand disturbance, 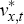 , as follows:
, as follows:
where: 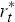 is the foreign nominal short-term interest rate; σ is strictly positive
and governs intertemporal substitution;
is the foreign nominal short-term interest rate; σ is strictly positive
and governs intertemporal substitution; 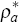 is the persistence
of
is the persistence
of 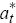 ;
;
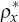 is the persistence of
is the persistence of 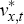 ; and ϕ1 defined
for notational convenience, is
; and ϕ1 defined
for notational convenience, is 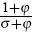 , with φ > 0 governing the
elasticity of labour supply.
, with φ > 0 governing the
elasticity of labour supply.
Foreign monetary policy follows a Taylor rule of the form
where 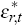 is an independent and identically distributed (iid) foreign monetary policy
shock, with zero mean and standard deviation
is an independent and identically distributed (iid) foreign monetary policy
shock, with zero mean and standard deviation 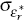 . Given the way in which
the policy rule is written,
. Given the way in which
the policy rule is written, 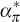 and
and 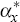 capture the short-run
reaction of
capture the short-run
reaction of 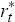 to the deviation of foreign inflation from
target (assumed to be zero) and the foreign output gap. So, values of
to the deviation of foreign inflation from
target (assumed to be zero) and the foreign output gap. So, values of 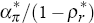 below unity correspond to violations of the Taylor principle and give rise to indeterminacy
of the equilibrium.
below unity correspond to violations of the Taylor principle and give rise to indeterminacy
of the equilibrium.
The potential level of foreign output, 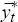 ,
is the level that would prevail in the absence of nominal rigidities. For the
large economy, it can be shown that the actual level of output,
,
is the level that would prevail in the absence of nominal rigidities. For the
large economy, it can be shown that the actual level of output, 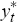 , and the output gap,
, and the output gap,
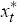 ,
obey
,
obey
Foreign exogenous processes evolve according to
where: the shocks 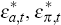 and
and 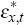 are iid with zero mean and standard deviations
are iid with zero mean and standard deviations 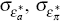 and
and 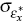 , respectively; the
auto-regressive parameters,
, respectively; the
auto-regressive parameters, 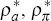 and
and 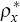 are less than unity
in absolute value.
are less than unity
in absolute value.
2.2 The Small Open Economy
In the small open economy, the IS-curve implies that the output gap, xt, is a function of its expected future value, the nominal interest rate, the expected rate of domestically produced goods inflation, the expected growth rate of foreign output, foreign and domestic aggregate demand shocks, and domestic total factor productivity. Following Galí and Monacelli (2005), one can show that the small open economy's IS-curve takes the form
where ρx and ρa are the persistence parameters of domestic demand and domestic productivity shocks, respectively. The parameters ρα, ϕ2, ϕ3 and ϕ4 are functions of deep parameters. In particular,
where: α Є [0,1] captures the degree of openness; τ is the intratemporal elasticity of substitution between foreign and domestically produced goods; and ι is the elasticity of substitution across varieties of foreign goods.[7]
The dynamics of domestically produced goods inflation, πh,t, are governed by an analogous Phillips curve equation
where: 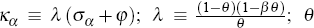 governs the degree of price stickiness; and νπ,t is a
cost-push shock.
governs the degree of price stickiness; and νπ,t is a
cost-push shock.
Monetary policy in the small economy is assumed to follow a Taylor rule that sets the nominal interest rate, rt, in response to its own lagged value, the deviation of consumer price inflation, πt, from its target (assumed to be zero), and the output gap, xt:
where εr,t is an iid monetary policy shock with
zero mean and standard deviation 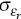 .
.
The terms of trade, st, are defined (from the perspective of the large economy) as the price of foreign goods, pf,t, in terms of the price of home goods, ph,t. That is, st = pf,t − ph,t. Around a symmetric steady state the consumer price index is a weighted average of the form pt = (1−α)ph,t + αpf,t. It is straightforward to show that pt = ph,t + αst. From this equation it follows that consumer price inflation and domestically produced goods inflation are linked by the expression
The nominal exchange rate, et, is defined as the price of foreign currency in terms
of the domestic currency. The real exchange rate, qt, in
turn, is defined as 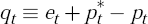 It then follows that changes in the nominal
exchange rate, Δet, can be decomposed into changes
in the real exchange rate and consumer price inflation differentials
It then follows that changes in the nominal
exchange rate, Δet, can be decomposed into changes
in the real exchange rate and consumer price inflation differentials
Positive values of Δet indicate a nominal depreciation of the domestic currency
as the price of the foreign currency increases. Because the law of one price
is assumed to hold 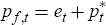 , which implies that the terms of trade can
also be written as
, which implies that the terms of trade can
also be written as 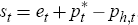 . Combining these expressions, it is easy
to show that the real exchange rate is proportional to the terms of trade.
Thus,
. Combining these expressions, it is easy
to show that the real exchange rate is proportional to the terms of trade.
Thus,
Complete international securities markets, together with the market clearing conditions, lead to the following relationship between the terms of trade, st, and output differentials and demand shock differentials: [8]
The presence of the aggregate demand shock differential in Equation (14), (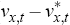 ),
alters the small economy's flexible price level of output, relative to
Galí and Monacelli
(2005).[9]
The relationship between the actual level of output, yt,
and the output gap, xt, satisfies the following equation:
),
alters the small economy's flexible price level of output, relative to
Galí and Monacelli
(2005).[9]
The relationship between the actual level of output, yt,
and the output gap, xt, satisfies the following equation:
Finally, the exogenous domestic processes evolve according to
where: the shocks, εa,t, επ,t and εx,t
are iid with zero mean and standard deviations 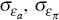 and
and 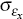 , respectively; the
auto-regressive parameters, ρa,ρπ
and ρx, are less than unity in absolute value.
, respectively; the
auto-regressive parameters, ρa,ρπ
and ρx, are less than unity in absolute value.
2.3 Calibration
The benchmark calibration of the model yields a unique REE and resembles that of Galí and Monacelli (2005).[10] Our calibration is loosely based on data from the US and Australia and falls within the range of chosen values in the literature. The values assigned to the structural parameters are summarised in Table 1.
| Price stickiness | θ = 0.75 |
|---|---|
| Discount factor | β = 0.99 |
| Intertemporal elasticity of substitution | σ = 1.50 |
| Share of foreign goods in CPI basket | α = 0.40 |
| Elasticity of substitution between foreign varieties | τ = 1.1 |
| Elasticity of substitution between domestic and foreign goods | ι = 1.2 |
| Elasticity of labour supply | φ = 2.0 |
| Interest rate smoothing | ρr = 0.90 |
| Output gap response | αx = 0.001 |
| Inflation response | απ = 0.125 |
| Interest rate smoothing (large) | 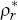 = 0.90 = 0.90 |
| Output gap response (large) | 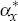 = 0.001 = 0.001 |
| Inflation response (large) | 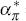 = 0.125 = 0.125 |
The shape – but not the size – of the impulse responses are invariant to the standard deviations of the fundamental disturbances. The set of optimal policy results, however, are sensitive to these values.
The exogenous processes described by Equations (5), (6), and (7) and their domestic
counterparts are known in the literature to be highly
persistent.[11]
We chose 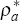 to 0.95,
to 0.95, 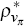 to 0.96,
to 0.96, 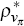 to 0.98, and ρα,
to 0.98, and ρα, 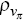 , and
, and 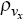 to 0.95.
to 0.95.
Given the parameter values in Table 1, we set the standard deviations of the shocks
in two steps. First, we calibrate the standard deviations of the large economy's
shocks as follows: 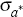 is set to 0.007 as suggested by Cooley and Prescott (1995).
is set to 0.007 as suggested by Cooley and Prescott (1995).
Then, 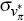 ,
,
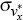 and
and 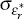 are chosen to minimise the sum of squares deviations of the theoretical standard
deviations of the interest rate, inflation, and the output gap from empirical
counterparts.[12]
The interest rate in the data is taken to be the quarterly average of the Federal
funds rate, foreign inflation is measured as the quarterly growth rate of the
US consumer price index, and the foreign output gap is measured as log deviations
of US real quarterly GDP per capita from a linear trend over the sample period
1980:Q1–2006:Q4. This strategy yields the values summarised in Table
2.
are chosen to minimise the sum of squares deviations of the theoretical standard
deviations of the interest rate, inflation, and the output gap from empirical
counterparts.[12]
The interest rate in the data is taken to be the quarterly average of the Federal
funds rate, foreign inflation is measured as the quarterly growth rate of the
US consumer price index, and the foreign output gap is measured as log deviations
of US real quarterly GDP per capita from a linear trend over the sample period
1980:Q1–2006:Q4. This strategy yields the values summarised in Table
2.
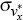 = 0.01982 = 0.01982 |
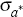 = 0.00700 = 0.00700 |
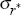 = 0.00002 = 0.00002 |
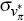 = 0.00071 = 0.00071 |
Second, we take the large economy's parameter values as given and calibrate the
standard deviation of the small economy's shocks in a similar way. The
value of σa is also set to 0.007, and 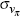 ,
, 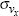 and
and 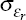 are set to minimise
the sum of squares deviations of the theoretical standard deviations of the
small economy's interest rate, consumer price inflation, and the output
gap from their empirical counterparts. For the small economy we use Australian
data and take these to be the quarterly average of the nominal cash rate, the
quarterly growth rate of the consumer price index, and log deviations of real
quarterly GDP per capita from a linear trend; once again, all series are taken
over the same sample period as before. This procedure yields the values summarised
in Table 3.
are set to minimise
the sum of squares deviations of the theoretical standard deviations of the
small economy's interest rate, consumer price inflation, and the output
gap from their empirical counterparts. For the small economy we use Australian
data and take these to be the quarterly average of the nominal cash rate, the
quarterly growth rate of the consumer price index, and log deviations of real
quarterly GDP per capita from a linear trend; once again, all series are taken
over the same sample period as before. This procedure yields the values summarised
in Table 3.
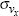 = 0.03713 = 0.03713 |
| σa = 0.00700 |
| σr = 0.00066 |
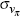 = 0.00002 = 0.00002 |
Footnotes
The terms foreign and large are used interchangeably. [5]
See Goodfriend and King (1997), Clarida, Galí and Gertler (1999), Woodford (2003) and Ireland (2004) for discussions of the new Keynesian closed economy model. [6]
We refer the reader to Galí and Monacelli (2005) for the non-linear expressions that contain these structural parameters. [7]
Demand shocks, νx,t, enter the household's lifetime expected
utility as follows: 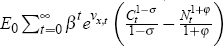 . Thus, one can show that aggregate demand
disturbances enter the international risk-sharing condition as in Equation
(14).
[8]
. Thus, one can show that aggregate demand
disturbances enter the international risk-sharing condition as in Equation
(14).
[8]
One could show that the level of potential output in the small economy is given by
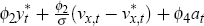 .
If aggregate demand shocks were absent from our model, the expression for
the output gap collapses back to that of Galí and Monacelli's.
[9]
.
If aggregate demand shocks were absent from our model, the expression for
the output gap collapses back to that of Galí and Monacelli's.
[9]
Galí and Monacelli set σ = τ = ι = 1. For this special case, the small economy's real marginal cost is completely insulated from movements in foreign output. We chose to select a more general calibration, although our main findings hold in this special case as well. [10]
See, for example, Ireland (2004). [11]
The criterion that we seek to minimise is of the form: 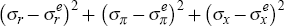 ,
where σi stands for the model-generated standard
deviation of variable i, and
,
where σi stands for the model-generated standard
deviation of variable i, and 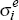 for its empirical
counterpart.
[12]
for its empirical
counterpart.
[12]