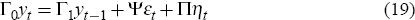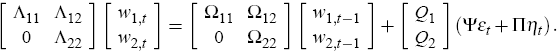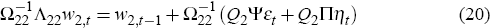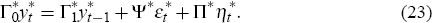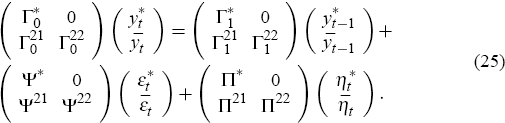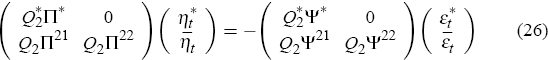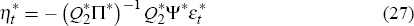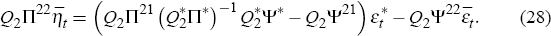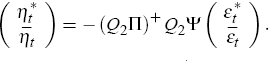RDP 2007-06: The Butterfly Effect of Small Open Economies 3. Stable Rational Expectations Equilibria
June 2007
- Download the Paper 247KB
3.1 Existence, Uniqueness and Multiplicity
For any variable, say πt, the expectational error, 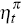 , is defined as πt
− Et−1πt, where
Et−1 is the expectations operator conditional
on information at t−1, and
, is defined as πt
− Et−1πt, where
Et−1 is the expectations operator conditional
on information at t−1, and 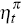 satisfies
satisfies 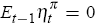 for all periods t.
As in Sims (2001), we collect the expectational errors in a k ×
1 vector ηt and write the model, given by Equations
(1) to (18), in matrix form as follows:
for all periods t.
As in Sims (2001), we collect the expectational errors in a k ×
1 vector ηt and write the model, given by Equations
(1) to (18), in matrix form as follows:
where εt is a l × 1 vector of fundamental serially uncorrelated random disturbances and the n × 1 vector yt contains the remaining variables, including conditional expectations.
Lubik and Schorfheide (2003) have extended Sims's (2001) solution for linear rational expectations models by characterising the full set of stable solutions. For completeness we provide a discussion below.
The QZ decomposition (generalised Schur decomposition) yields unitary matrices (complex matrices with orthonormal columns) Q and Z, and upper-triangular matrices Λ and Ω such that Γ0=Q′ΛZ′ and Γ1=Q′ΩZ′. An important by-product of this decomposition is that it gives the generalised eigenvalues of Γ0 and Γ1 as the ratios of the diagonal elements of the matrices Λ and Ω.[13]
Next, we define a new set of variables, wt = Z′yt, and partition the resulting system into the m variables whose generalised eigenvalues are greater than 1, w2,t, and those whose generalised eigenvalues are less than 1, w1,t. Then, in Equation (19), we substitute the matrices Γ0 and Γ1 for their QZ decompositions and pre-multiply by Q to obtain
In the expression above, the bottom set of equations, which can be rewritten as
governs the behaviour of the m × 1 vector of purely explosive variables, w2,t. For the system to be stable, the expectational errors, ηt, have to offset the impact that fundamental shocks, εt, have on the purely explosive variables, w2,t. In other words, a stable solution requires that in all periods t,
Every possible l × 1 vector of fundamental shocks, εt, gives rise to a new m × 1 vector −Q2Ψεt; and for every possible −Q2Ψεt, Equation (21) asserts that there exists a combination of the columns of Q2Π capable of producing exactly −Q2Ψεt. As Sims (2001) shows, a stable solution to Equation (19) exists if, and only if, each of the columns of Q2Ψ can be obtained as linear combinations of the columns of Q2Π.[14]
Note that Q2Π has dimensions m × k. So there are m equations and k expectational errors to be determined. If the number of explosive variables, m, equals the number of expectational errors, k, and each of the m equations is independent of one another, then Q2Π is a full rank matrix and the expectational errors are unique linear combinations of the fundamental shocks. That is,
In this case, Equation (19) has a unique solution and the dynamics of yt are exclusively driven by fundamental shocks.
It is possible, however, that Equation (21) does not determine ηt in a unique manner. For instance, if k exceeds m, Equation (21) can be satisfied for infinitely many values of ηt. In this way, the system admits expectational errors that are unrelated to the fundamental disturbances.
Even in the complete absence of fundamental shocks, expectational errors can become a source of fluctuations. To see this, suppose that k > m and εt = 0 for all t. Then Equation (21) reduces to the homogeneous system Q2Πηt = 0. Since there are more unknowns than equations, it follows that Q2Πηt = 0 has a non-trivial solution (ηt ≠ 0), and, in fact, infinitely many of them. Continue to assume that εt = 0 and ηt ≠ 0 for all t, then Equation (19) becomes Γ0yt = Γ1yt−1 + Πηt, which explicitly shows that the dynamics of yt are, in this case, exclusively a function of non-fundamental shocks.
Formally, the variation in ηt that may arise under indeterminacy, and that is unrelated to the variation in εt is the result of sunspot shocks, which we denote ξt.[15]
3.2 Expectations and Size
The small open economy model given by Equations (1) to (18) has a particular structure meant to capture the size differences of the two economies. The large economy, described by Equations (1) to (7), can be solved in isolation without reference to any other equation in the system. Thus, the large economy can be written as a self-contained system as follows:
Proceeding as before, the stability condition of the large economy is
Note that if the solution to Equation (24) is unique, the k* foreign expectational errors, 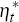 , are, exclusively,
linear combinations of the l* foreign fundamental shocks,
, are, exclusively,
linear combinations of the l* foreign fundamental shocks, 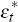 .
.
It is possible to partition yt into the n* foreign variables,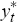 , and
, and 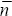 remaining ones,
remaining ones, 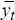 ;
εt and ηt can be partitioned
in a similar manner, so that Equation (19) can be written as follows:
;
εt and ηt can be partitioned
in a similar manner, so that Equation (19) can be written as follows:
The dimensions of the sub-matrices, 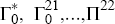 ,
are conformable to the partition. The stability condition in its partitioned
form satisfies
,
are conformable to the partition. The stability condition in its partitioned
form satisfies
and the sub-matrices conform also to the partition obtained from the QZ decomposition: 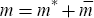 .
.
If the equilibrium of the large economy is unique, it follows that
which, in turn, implies that we can solve the second set of equations in Equation (26) as
Equations (27) and (28) highlight an important aspect of the structure of the model:
uniqueness in the large economy is sufficient to ensure that its dynamics are
driven only by its fundamental shocks, regardless of whether or not the small
economy's expectational errors, 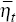 ,
are uniquely determined by its fundamentals. As one would expect, indeterminacy
which originates in the small economy does not affect the equilibrium dynamics
of the large economy. The converse, as one would also expect, is that indeterminacy
caused by the large economy affects the determination of
,
are uniquely determined by its fundamentals. As one would expect, indeterminacy
which originates in the small economy does not affect the equilibrium dynamics
of the large economy. The converse, as one would also expect, is that indeterminacy
caused by the large economy affects the determination of 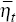 and the dynamics of
the small economy.
and the dynamics of
the small economy.
Surprisingly, perhaps, indeterminacy arising in the large economy opens up a channel
through which shocks to the small economy, 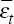 ,
influence the determination of
,
influence the determination of 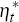 , and therefore the dynamics of the large
economy. Put differently, foreign indeterminacy allows the small economy's
shocks,
, and therefore the dynamics of the large
economy. Put differently, foreign indeterminacy allows the small economy's
shocks, 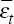 ,
to act exactly like non-fundamental shocks for the large economy. The small
economy's shocks,
,
to act exactly like non-fundamental shocks for the large economy. The small
economy's shocks, 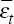 , can be described in this way because they
do not influence the dynamics of the large economy under uniqueness. This is
the ‘butterfly effect’: a situation in which the failure to pin
down the equilibrium of the large economy allows developments in the small
economy to affect developments in the large one.
, can be described in this way because they
do not influence the dynamics of the large economy under uniqueness. This is
the ‘butterfly effect’: a situation in which the failure to pin
down the equilibrium of the large economy allows developments in the small
economy to affect developments in the large one.
To see this mechanism, consider Equation (26), and assume that m* < k* and 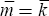 .
Clearly, indeterminacy in the large economy translates into indeterminacy for
the whole system because m < k. In this case, Q2Π
is not an invertible matrix because of the rank deficiency stemming from the
large economy's equations. Nevertheless, the full set of solutions can
be calculated with the generalised inverse of Q2Π, which
we denote by
(Q2Π)+:[16]
.
Clearly, indeterminacy in the large economy translates into indeterminacy for
the whole system because m < k. In this case, Q2Π
is not an invertible matrix because of the rank deficiency stemming from the
large economy's equations. Nevertheless, the full set of solutions can
be calculated with the generalised inverse of Q2Π, which
we denote by
(Q2Π)+:[16]
It is important to observe that the decrease in m* caused by foreign indeterminacy (relative to the m* = k* case), removes a set of zero-restrictions from Equation (26) – restrictions that were necessary to isolate the large economy from the small one.
Formally, the vector of expectational errors, ηt, belongs to 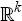 . For the sub-vector
. For the sub-vector 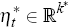 to equate to the same
value as the one that would have been obtained had we solved for the foreign
system (Equation (23)) in isolation, none of the zero-restrictions that show
up in the full rank version of Equation (26) can be removed. The ‘butterfly
effect’ appears because, in solving for ηt in
to equate to the same
value as the one that would have been obtained had we solved for the foreign
system (Equation (23)) in isolation, none of the zero-restrictions that show
up in the full rank version of Equation (26) can be removed. The ‘butterfly
effect’ appears because, in solving for ηt in
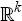 , foreign
indeterminacy effectively takes away some of the zero-restrictions that were
necessary to obtain the same solution for
, foreign
indeterminacy effectively takes away some of the zero-restrictions that were
necessary to obtain the same solution for 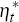 that would have been
obtained had we solved for the large economy in isolation, in
that would have been
obtained had we solved for the large economy in isolation, in 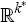 .
.
If the large economy is solved in isolation under indeterminacy, the ‘butterfly
effect’, of course, can never occur. To justify this approach requires
the additional assumption that agents in the large economy form their expectations
solely on the basis of information from that economy alone. In this case, the
set of multiple solutions of the large economy can be computed with the generalised
inverse of 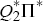 .
The foreign expectational errors are then given by
.
The foreign expectational errors are then given by 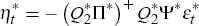 , in which case
, in which case 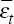 ,
by construction, can never influence
,
by construction, can never influence 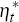 .[17]
Solving the large economy first and then using its solution as an exogenous
process for the small economy, or solving them simultaneously, is equivalent
only if the equilibrium of the large economy is unique.
.[17]
Solving the large economy first and then using its solution as an exogenous
process for the small economy, or solving them simultaneously, is equivalent
only if the equilibrium of the large economy is unique.
Thus, uniqueness of the large economy's equilibrium constrains the formation of expectations to a subset of the full information set. ‘Smallness’ is then a property that emerges from the unique determination of the large economy's equilibrium, but not a general property of the system.
Footnotes
A standard eigenvalue problem is of the form Ax = λx. A generalised eigenvalue problem takes the form Ax = μBx. The values of μ that satisfy this last equation are called the generalised eigenvalues of A and B. [13]
Sims's condition is actually more general because it allows any pattern of serial correlation in εt. The condition reduces to Equation (21) under our assumption of serially uncorrelated disturbances. Unless otherwise stated, the existence condition given by Equation (21) always holds in our analysis. Stability also requires the initial condition w2,0 = 0. [14]
See Lubik and Schorfheide (2003) for an expression of the expectational errors as linear combinations of fundamental shocks, εt, and non-fundamental shocks, ξt. The only restriction on the distribution of sunspots shocks is that they follow a martingale difference sequence; that is, Et–1ξt = 0. [15]
The solution shown above is the minimum distance solution which satisfies Equation (21). The general solution to the inhomogeneous system Q2Πηt = −Q2Ψεt is the sum of a particular solution of the inhomogeneous system and the general solution of the corresponding homogeneous system Q2Πηt = 0. Under the assumption that Q2Π is a full row rank matrix, (Q2Π(Q2Π)′)−1 exists. Then the solution ηt can always be written as the sum of the generalised inverse solution of the inhomogeneous system and a solution of the homogeneous system: ηt = −(Q2Π)+Q2Ψεt + (I − (Q2Π)′(Q2Π(Q2Π)′)−1Q2Π)zt, where the vector zt is arbitrary (apart from its dimensionality). [16]
The solution shown here is the minimum distance solution which satisfies Equation
(24). The general solution to the inhomogeneous system given by Equation
(24) is the sum of a particular solution of the inhomogeneous system and
the general solution of the corresponding homogeneous system 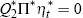 .
[17]
.
[17]