RDP 2008-03: Monetary Transmission and the Yield Curve in a Small Open Economy 4. The Dynamics of the Yield Curve

Figure 2 shows the impulse responses to a domestic technology shock of the small economy's yield curve for two different parameterisations of persistence: ρ_a = 0.9 and ρ_a = 0.65.^[12] The less persistent the shock, the smaller the impact on longer-term rates. The intuition for this is straightforward: less persistent shocks induce less persistent expected movements of the short-term rate.

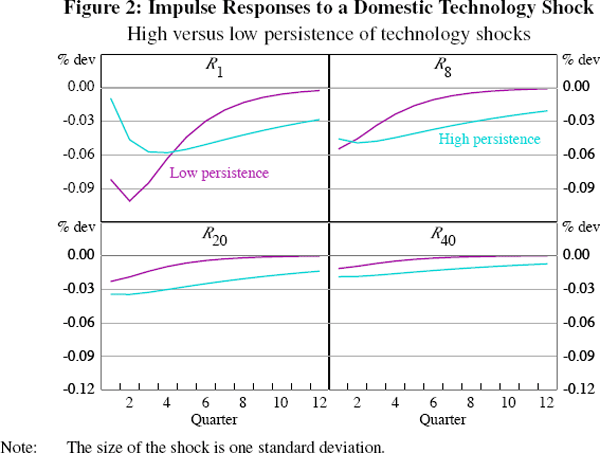
Perhaps less obvious is the fact that a less persistent shock moves shorter-term rates on impact by more than a more persistent shock. One way to understand the intuition here is to consider the role of consumption smoothing in response to a positive technology shock. For very persistent shocks, consumption should rise by almost as much as output (since the shock to income is long lasting), hence the output gap is little changed and the monetary policy response can be relatively modest. However, for a temporary shock, much of the extra income will be saved, leading to a decline in the output gap and hence monetary policy will respond by cutting short-term interest rates.^[13]

The key to understanding the model's ability to reproduce the pattern of correlations in Figure 1 is that less persistent domestic shocks produce a source of variation in the yield curve that is relatively stronger at the short end of the yield curve than at the long end. Other things equal, if the persistence of a domestic shock decreases, the correlation between the short-term rates of the two economies would decrease, while the correlation between their longer-term rates would increase. The correlation at the long end increases because, if the persistence of domestic shocks decreases, foreign shocks – the cause of variability of foreign rates – become a relatively more important source of variation for domestic long-term rates. Also note that domestic shocks, regardless of their persistence, are a source of variation for the domestic yield curve but not one for the foreign yield curve.^[14] Thus, the larger the variance of domestic shocks relative to that of foreign shocks, the smaller (in absolute value) the correlation between domestic and foreign interest rates.

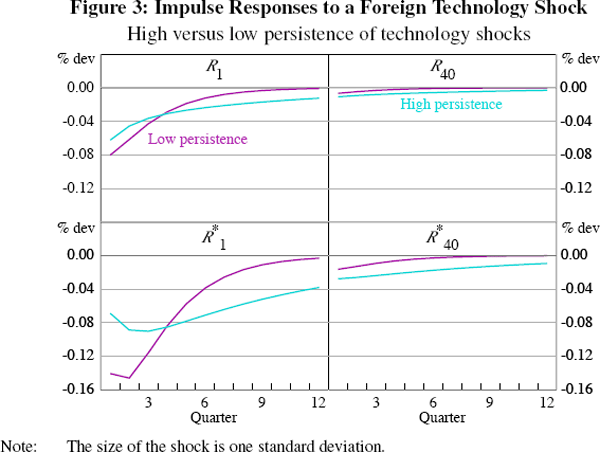
Figure 3 shows impulse responses of both domestic and foreign yield curves for two different parameterisations of the persistence of the foreign technology process: 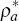= 0.9 and 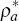= 0.65. As before, the less persistent the shock, the smaller the impact on both foreign and domestic longer-term rates and the larger the impact on both foreign and domestic short-term rates. Clearly, foreign shocks, unlike domestic ones, constitute a source of variation for both yield curves and therefore drive up the overall level of co-movement between interest rates of all maturities and currencies. But, for the model to be able to produce the upward-sloping pattern of correlations in Figure 1, foreign shocks have to be relatively more persistent than domestic shocks.

Footnotes

All other parameters are set at the estimated posterior mean values of Tables 1 and 2. [12]

Note that the coefficient on the technology shock in Equation (8) is (1 − ρ_a), so in the extreme case in which ρ_a = 0, the contemporaneous impact of the shock would be the highest possible. [13]

We confine our attention to unique rational expectations solutions in which the large economy is exogenous to the small one. See Jääskelä and Kulish (2007) for a discussion of non-uniqueness in this model. [14]