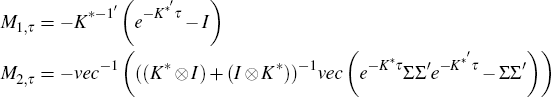RDP 2008-09: A Term Structure Decomposition of the Australian Yield Curve Appendix C: Model Implementation
December 2008
- Download the Paper 579KB
C.1 Formulas for aτ and bτ
From Kim and Orphanides (2005) we take the following formulas (with corrections):
where
with  vec taking a matrix to a vector column-wise, and vec−1
doing the opposite.
vec taking a matrix to a vector column-wise, and vec−1
doing the opposite.
C.2 The Kalman Filter
Our implementation of the Kalman filter is based on that used by Duffee and Stanton (2004). The recursion goes from t = 1 forward, and is as follows:
-
Using the current value of xt, compute
the one-step-ahead forecast of xt, given
by
 ,
and its variance matrix
,
and its variance matrix  .
.
-
Compute the one-step-ahead forecast of yt,
given by
 , and its variance matrix
, and its variance matrix  , where R
is the zero-coupon bond measurement error variance matrix.
, where R
is the zero-coupon bond measurement error variance matrix.
-
Compute the forecast errors of
 , given by
, given by  .
.
-
Update the prediction of xt+1 with
 and the variance with
and the variance with  .
.
For times t when we have analysts' forecasts, replace yt,
a, B and R by  and
and  , respectively.
, respectively.
We then choose our parameter vector Θ to solve
where the sample is n periods long, and the period-t approximate log-likelihood is given by
C.3 Implementation
To implement the model we restrict the parameters to those which result in K and K* having positive eigenvalues. This results
in e−Ks → 0 and  as s →
∞, which ensures the stability of the model (see Equation (9) and the
formulas for aτ and bτ).
We also require that the σi, being variances,
are positive.
as s →
∞, which ensures the stability of the model (see Equation (9) and the
formulas for aτ and bτ).
We also require that the σi, being variances,
are positive.
By way of parameter choices that must be made, we set x1 = [0.005, 0.03, 0.01]′ (with an initial standard deviation of 10 per cent) and then discard the first six months of the estimation. The standard deviation of zero-coupon yield measurement errors is set to 10 basis points, while those of the survey forecasts are set to 50 basis points per square root year.
Finally, the standard errors in Tables 1 and 2 are calculated using a random walk chain Metropolis-Hastings algorithm – for details see Geweke (1992).