RDP 2010-01: Reconciling Microeconomic and Macroeconomic Estimates of Price Stickiness 3. The Data-generating Process
March 2010
- Download the Paper 462KB
In this section, we sketch the model we use as the data-generating process for our evaluation of the effect of heterogeneity and roundabout production on the GMM estimates of the NKPC. We also discuss parameter selection, compare moments of the model to moments in the data and briefly explore the properties of the model with and without heterogeneity and roundabout production.
3.1 The Model
The model is similar to those used by Carvalho (2006) and Nakamura and Steinsson (2009), which both incorporate heterogeneity in the average duration of prices across firms. However, our approach differs in a number of respects. For example, we deviate from Nakamura and Steinsson (2009) by assuming that pricing is time-dependent.[2] Our model also incorporates a wider number of shocks than both Carvalho (2006) and Nakamura and Steinsson (2009), many of which are typically found in DSGE models.
The basic foundations of the monetary model described below are standard in the literature (for example, Ireland 2004). We add roundabout production as well as heterogeneity in Calvo price setting and technology. The model is described briefly below (a full description is provided in Appendix A).
The model contains the following agents:
- households, who are modelled in a standard way;
- final-goods firms, that produce final goods from intermediate goods;
- intermediate-goods firms, that produce intermediate goods for other intermediate-goods firms and final-goods firms; and
- a monetary authority.
Final-goods producers are perfectly competitive and use constant elasticity of substitution technology to produce final goods from intermediate goods, which they obtain from intermediate-goods firms in a particular sector. There is a continuum of monopolistically competitive intermediate-goods producers, indexed on the interval (0, 1]. We segment this interval into a finite number of partitions, each representing a particular sector of the economy.
A characteristic of modern economies is a complex interdependence between firms within and across sectors of the economy.[3] In our model, goods produced by intermediate-goods firms in one sector can be used by other firms in that sector, by other intermediate-goods firms operating in other sectors and by the final-goods producers who only source their inputs from that sector. Intermediate-goods producers also use labour supplied by households. The monetary authority sets the interest rate as a function of inflation and growth in consumption (value added).
Each sector of the economy is characterised by its own production technology and Calvo probability (θj). Production of intermediate goods is characterised by Cobb-Douglas technology, with the factor shares for labour and for intermediate goods varying across sectors. This means that in the steady state, labour cost shares, marginal costs and prices will be sector-dependent.
The model incorporates four sources of uncertainty (in addition to that implied by the Calvo pricing mechanism):
- a consumption preference (demand) shock;
- an aggregate non-stationary technology process for intermediate-goods producers;
- sector-specific technology shocks for intermediate-goods producers; and
- a monetary policy shock.
3.2 Parameter Selection
The parameters of the model are mostly calibrated, reflecting our goal of creating a model to simulate realistic data, rather than to precisely estimate the true data-generating process.
A key part of the model is the heterogeneity in the Calvo probability across sectors. We calibrate the Calvo probability for each sector by using data collected by the Reserve Bank of Australia through a survey of firms. Briefly, the survey recorded 438 responses to a questionnaire on price setting from June 2000 to April 2006.[4] The survey contains the median number of price adjustments over 12 months and we compute the implied quarterly Calvo probabilities (θj) from the frequency of price changes reported by firms.
The survey asks the question ‘how many times has the firm actually changed prices in the last 12 months?’, which does not distinguish between price changes caused by sales or product substitutions. We assume that there is no indexation of prices consistent with microeconomic price behaviour in databases such as Dominick's Finer Food Database and the CPI Research Database (Midrigan 2007; Klenow and Kryvtsov 2008).[5] Table 1 presents the median number of price adjustments over 12 months and the associated Calvo probability for each sector.
The size of sector j is denoted by γj. In conjunction with
the labour shares of income, these size parameters govern sectors' steady-state
shares of labour and intermediate inputs. We choose these size parameters to
try and match these shares to the data. Because there are 9 size parameters
and essentially 28 moments, we cannot match all of these moments. Instead,
we minimise the weighted average of the difference between the implied steady
shares and those in the data. The moments reflecting each sector's share
of labour, intermediate input shares and gross revenue are taken from the Australian
Bureau of Statistics (ABS) over the period 1995–2003. The economy-wide
steady-state share of value added in gross output, 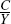 , is 0.41 in the data
whereas our choice of parameters implies 0.48. The results are shown in Table
2.[6]
, is 0.41 in the data
whereas our choice of parameters implies 0.48. The results are shown in Table
2.[6]
| Gross revenuec | Hours worked | Intermediate inputs | ||||||
|---|---|---|---|---|---|---|---|---|
| Sector | Data | Calibrated | Data | Calibrated | Data | Calibrated | ||
| Agriculture | 0.05 | 0.06 | 0.09 | 0.05 | 0.04 | 0.06 | ||
| Construction | 0.14 | 0.15 | 0.12 | 0.10 | 0.17 | 0.17 | ||
| Manufacturing | 0.28 | 0.29 | 0.22 | 0.25 | 0.33 | 0.30 | ||
| Mining | 0.06 | 0.05 | 0.02 | 0.03 | 0.04 | 0.05 | ||
| Utilities | 0.03 | 0.03 | 0.01 | 0.02 | 0.03 | 0.03 | ||
| Wholesale and retail trade | 0.18 | 0.19 | 0.28 | 0.26 | 0.16 | 0.17 | ||
| Transport and storage | 0.08 | 0.08 | 0.08 | 0.07 | 0.08 | 0.09 | ||
| Business services | 0.12 | 0.07 | 0.09 | 0.12 | 0.08 | 0.06 | ||
| Household services | 0.05 | 0.05 | 0.07 | 0.06 | 0.05 | 0.05 | ||
| Tourism | 0.02 | 0.02 | 0.03 | 0.03 | 0.02 | 0.02 | ||
|
Notes: (a) Numbers presented are each sector's share of the total over
the period 1995–2003 and their corresponding calibrated values.
Values do not sum to 1 in the table because of rounding errors. Sources: ABS – Australian National Accounts: Input-Output Tables (Cat No 5209.0.55.001); Labour Force, Australia, Detailed, Quarterly (Cat No 6291.0.55.003); Experimental Estimates of Industry Multifactor Productivity (Cat No 5260.0.55.002); authors' calculations |
||||||||
In order to calibrate each sector's technology parameters, we use the annual experimental estimates of multifactor productivity (MFP) by sector as published by the ABS in 2007. Because the sectoral technology is assumed to follow a stationary quarterly AR(1) process in our model, we quadratically interpolate the data to obtain a quarterly series. We then detrended the logarithm of the quarterly series and estimated the AR(1) process for each sector from the filtered series. The calibrated values for the steady-state shares and estimated parameters describing sector technology are displayed in Table 3. We also use the market sector MFP series to calibrate the standard deviation of aggregate technology shock.
| Sector |
Persistence (ρj) |
Technology shocks std deviation (σz j) | Labour share of income (αj) |
|---|---|---|---|
| Agriculture | 0.83 | 3.91 | 0.29 |
| Construction | 0.88 | 1.46 | 0.24 |
| Manufacturing | 0.86 | 0.60 | 0.29 |
| Mining | 0.80 | 1.71 | 0.24 |
| Utilities | 0.93 | 0.53 | 0.24 |
| Wholesale and retail trade | 0.88 | 0.50 | 0.39 |
| Transport and storage | 0.87 | 0.61 | 0.29 |
| Business services | 0.91 | 0.61 | 0.44 |
| Household services | 0.79 | 0.69 | 0.35 |
| Tourism | 0.91 | 0.80 | 0.39 |
|
Sources: ABS – Information Paper: Experimental Estimates of Industry Multifactor Productivity (Cat No 5260.0.55.001); updated in Cat No 5260.0.55.002; authors' calculations |
|||
We set the Frisch elasticity of labour supply to one-half, consistent with the parameter values used in Carvalho (2006). Based on the industrial organisation and international trade literature, we set the elasticity of substitution to 4 (a one-third mark-up) as in Nakamura and Steinsson (2009). See Table 4 for a list of calibrated and estimated parameters not available directly from the data.
| Parameter | Description | Value | Std error |
|---|---|---|---|
| Calibrated | |||
| β | Household discount factor | 0.99 | – |
| ε | Elasticity of substitution | 4.00 | – |
| η | Frisch Elasticity of labour supply | 0.50 | – |
| σz | Std deviation of aggregate technology shock | 0.44 | – |
| Estimated | |||
| ρi | Persistence of the nominal interest rate | 0.71 | 0.04 |
| øπ | Long-run response of policy rate to inflation | 1.16 | 0.13 |
| øg | Long-run response of policy rate to growth | 0.21 | 0.11 |
| ρa | Persistence of preference shocks | 0.89 | 0.07 |
| σi | Std deviation of interest rate shock | 0.12 | 0.02 |
| σa | Std deviation of preference shock | 0.40 | 0.11 |
|
Source: authors' calculations |
|||
The log-linearised rational expectations model is solved using the method outlined in Sims (2002). We estimate the remaining parameters of the model, namely the monetary policy rule parameters, the persistence of the preference shocks and the standard deviations of some aggregate shocks, by maximum likelihood using the Kalman filter (see Hamilton 1994). The Kalman filter is required because we treat most of the variables in the model as unobservable; for example, many of the real variables in the log-linearised model have been detrended by the unobserved non-stationary aggregate technology series. The rational expectations solution to the model dictates how the model variables evolve over time and the relationships between them. The Kalman filter is used to estimate the unobserved series in a manner consistent with both the reduced form of the model and the observed variables, which include growth in GDP per capita, the overnight cash rate and headline CPI inflation (excluding taxes and volatile items) over the period 1993:Q1 to 2007:Q4.
3.3 Properties of the Model
3.3.1 Hazard functions
The hazard function for price changes describes the probability of a price change at time t given that the price has not changed between period 0 and period t – 1. Comparing the characteristics of the hazard function from a model to that estimated from microeconomic data is a simple way of assessing the validity of the model's description of price-setting behaviour.
Klenow and Kryvtsov (2008) and Nakamura and Steinsson (2008), using the microeconomic data underlying the US CPI, find that the aggregate hazard function is downward-sloping. That is, prices are less likely to change the longer they remain unchanged. Klenow and Kryvtsov (2008) argue that the result is likely to reflect heterogeneity, and once this is taken into account the estimated aggregate hazard function is flat.
The Calvo model predicts that the probability of a firm changing its price is independent of its duration, and therefore hazard functions, both at the product and aggregate level, are flat. Alternatively, by allowing for heterogeneity in the Calvo probability across sectors our model is capable of replicating the results of Klenow and Kryvtsov (2008), namely flat product-level hazard functions and a downward slope for the aggregate hazard function, which we demonstrate analytically in Appendix C. Our model therefore can generate an important characteristic of the microeconomic pricing data that the standard Calvo model cannot.
3.3.2 Empirical results
We compare the properties of four variations of our model in order to disentangle the effects of heterogeneity and roundabout production:
- (Baseline) A version of our model with labour as the only input to intermediate-goods production (that is, no roundabout production) and sectors that are homogeneous in every other respect.
- (Heterogeneous) This version adds heterogeneity in the Calvo probability and sectoral technology shocks but there is no roundabout production technology in the model.[7]
- (Roundabout) Roundabout technology is added to the baseline model so that intermediate-goods producers use other intermediate goods in production. However, this variation treats all sectors as homogenous so that the Calvo probabilities are uniform across sectors and there are no sector-specific technology shocks.[8]
- (Full) The full model includes roundabout technology, heterogeneity in Calvo probabilities and production technology as well as sector-specific technology shocks.
Our results can be summarised by the moments of the various models and the impulse response functions.
Table 5 presents actual and simulated moments for some of the key variables, namely growth in GDP per capita (gt), inflation (πt) and the nominal interest rate (it). The full model broadly matches the univariate moments of the data shown (compare the first column – the actual data – and the last). The magnitudes of the contemporaneous cross-correlations are not as well matched, but are correctly signed.
| Parameter | Actual | Baseline | Heterogeneous | Roundabout | Full |
|---|---|---|---|---|---|
| Var(gt) | 0.33 | 0.22 | 0.32 | 0.25 | 0.33 |
| Var(πt) | 0.05 | 0.13 | 0.16 | 0.08 | 0.06 |
| Var(it) | 0.05 | 0.02 | 0.04 | 0.02 | 0.03 |
| Corr(gt, πt) | −0.01 | 0.03 | −0.20 | 0.16 | 0.06 |
| Corr(gt, it) | −0.12 | 0.07 | −0.04 | 0.03 | −0.02 |
| Corr(it, πt) | 0.27 | 0.33 | 0.43 | 0.24 | 0.32 |
| Corr(gt, gt−1) | −0.04 | −0.01 | 0.00 | −0.04 | −0.03 |
| Corr(it, it−1) | 0.93 | 0.89 | 0.89 | 0.87 | 0.87 |
| Corr(πt, πt−1) | 0.42 | 0.20 | 0.23 | 0.42 | 0.48 |
|
Notes: The moments are asymptotic except for those for actual data. The sample for the actual data is 1993:Q1 to 2007:Q4. Sources: ABS; authors' calculations |
|||||
An effect of roundabout production is to increase the persistence of inflation to the magnitude that is evident in the data – the autocorrelation of inflation is 0.42 in the roundabout model, compared to 0.20 in the baseline model (Table 5). This occurs because the output of each intermediate-goods firm, whose price is sticky, is an input to the production of other goods. Consequently, the marginal costs of intermediate-goods firms, and hence inflation, are more persistent.
It is also noticeable that volatility of growth in value added is larger in the heterogeneous model. This may partially reflect that in addition to introducing variation in the Calvo parameter, this model also incorporates a larger set of shocks than the baseline model, such as sector-specific technology processes. The volatility of growth in value added in the full model is in line with that observed in the data.
We can also compare the four models by examining their impulse response functions. Figure 1 illustrates the paths of key variables relative to their steady-state values. To facilitate comparison, the standard deviations of the shocks are those estimated for the full model. Note that the initial response of the interest rate across the models to the same-sized monetary policy shock can be different because the response of inflation, and other variables, in the model will differ. Also note that a positive aggregate technology shock increases growth in value added and reduces inflation. Because this is a permanent shock, the steady-state level of value added increases, however, since prices are sticky initially, there is not a commensurate increase in actual value added, which falls below its steady-state level.
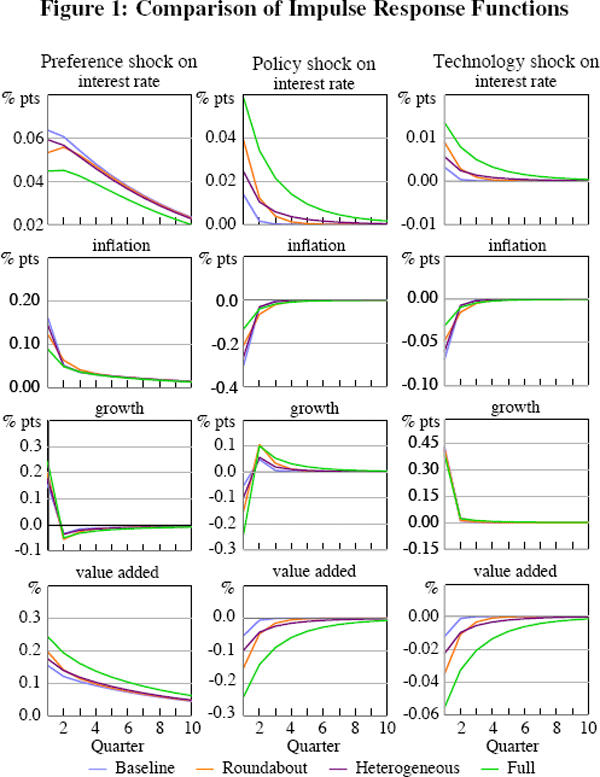
It is clear that heterogeneity and roundabout production make a difference to the response of value added (which is equivalent to consumption in these models). This is because both heterogeneity and roundabout production lead to relatively more muted responses of inflation to the shocks; as prices take longer to respond, the bulk of the short-run effects of shocks manifests in quantities rather than prices. When heterogeneity and roundabout production are combined the two features appear to increase the response of value added to aggregate shocks even further.
Heterogeneity leads to muted price responses because the firms with stickier prices have a disproportionately large effect on those firms with more flexible prices (Carvalho 2006).[9] This is consistent with profit maximisation since firms generally try not to change their prices too much relative to their competitors. The firms with stickier prices change their prices by less in response to shocks. Even though firms in the more flexible-price sectors can alter their prices more frequently, they have an incentive to keep their prices close to their slow moving competitors. The result is that aggregate prices in a model with heterogeneity in price setting appear to respond less to shocks compared to a model where all firms adjust their prices with the same average frequency. This is apparent in Figure 1 with inflation responding by less in the heterogenous model compared with the baseline model, and by less in the full model compared with the roundabout model.
The inertia in prices implied by heterogeneity and roundabout production implies that unexpected changes in monetary policy will have a larger affect on output (value added). Indeed, we find that when only policy shocks are present, the variance of value added increases by almost thirty-three times (from 0.003 to 0.09 percentage points) when heterogeneity and roundabout production are included. This is consistent with Nakamura and Steinsson (2009) who find that the presence of these two features increases the potency of monetary policy. In contrast, using a single-sector menu cost model, Golosov and Lucas Jr (2007) found that ‘... in none of the simulations we conducted did monetary shocks induce large or persistent real responses’.
Footnotes
They do, however, consider a limiting case with large adjustment costs as an approximation to the Calvo model, which they refer to as the CalvoPlus model. [2]
Input-output tables clearly show that a large share of the output of firms is used as an input by other firms from the same sector. As an example, firms in the business services sector in Australia source about 70 per cent of their intermediate inputs from other firms in that same sector. In the typical tiered approach to modelling production, the output of firms in a sector is used only by firms in other sectors. [3]
As the survey tries to match population characteristics, the number of responses from firms in the utilities and agriculture sectors is low. [4]
‘Backward indexation of prices, an assumption which, as far as I know, is simply factually wrong, has been introduced to explain the dynamics of inflation’ (Blanchard 2009, p 25). Also see Chari, Kehoe and McGrattan (2009). [5]
Note that the labour shares of income for the various sectors are lower than the aggregate measure from the national accounts as they are parameters in a gross output, rather than value-added, production function. [6]
Consequently, labour is the only factor of production, and its share of income, αj, is 1 for all j. The absence of intermediate
inputs also implies that 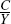 = 1.
[7]
= 1.
[7]
We set the Calvo probability to 0.3 in the roundabout and baseline models, which
is the  reported in Table 1.
[8]
reported in Table 1.
[8]
Heterogeneity in the Calvo probability was also studied in a structural model by Carvalho (2006). He found that in order to replicate the empirical impulse responses from a model incorporating heterogeneity, the degree of price stickiness would have to be increased by approximately threefold in a model that ignores this source of heterogeneity. Our paper shows that failing to account for heterogeneity will result in common econometric methods of estimating the NKPC – such as the Generalised Method of Moments (GMM) used by Galí and Gertler (1999) – sizeably overstating the degree of price stickiness. [9]