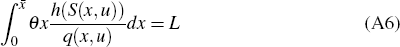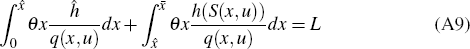RDP 2011-03: Urban Structure and Housing Prices: Some Evidence from Australian Cities Appendix A: Model Calibration
September 2011
- Download the Paper 613KB
We solve the model using Mathematica. The code is available on request.
Notation
x is the location as measured by distance from the center of the city,
which is x = 0; 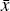 is the distance to the urban-rural boundary;
t > 0 is the commuting cost parameter; y is an exogenously
determined annual wage; q is the consumption of housing measured in
floor space per dwelling; p is the price per square metre of housing
[27]; c
is the consumption of a bundle of other goods with its price normalised to
unity; h is housing production measured in housing floor space per
unit of land; l is the input of land into the production of housing;
K is the input of capital into the production of housing; S
is the capital-land ratio K/l ; r is the rental
price of land; i is the exogenously determined rental rate on capital;
L is the city's population.
is the distance to the urban-rural boundary;
t > 0 is the commuting cost parameter; y is an exogenously
determined annual wage; q is the consumption of housing measured in
floor space per dwelling; p is the price per square metre of housing
[27]; c
is the consumption of a bundle of other goods with its price normalised to
unity; h is housing production measured in housing floor space per
unit of land; l is the input of land into the production of housing;
K is the input of capital into the production of housing; S
is the capital-land ratio K/l ; r is the rental
price of land; i is the exogenously determined rental rate on capital;
L is the city's population.
Demand for housing
The representative individual maximises utility, v(c,q), by consuming housing and a bundle of other goods, subject to the budget constraint, pq + c = y − tx. The optimality conditions of the households problem are
and
Equations (A1) and (A2) give solutions for q and p as functions of y, t, u and x.
Supply of housing
At a particular location x, a housing producer generates profit l (ph(S) − r − iS). The first order conditions from profit maximization are given by
and
Equations (A3) and (A4) give solutions for S and r.
Equilibrium
The equilibrium conditions determine the level of welfare, u, and the city boundary, 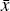 . They require that
the rental price of land at
. They require that
the rental price of land at 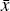 equals the agricultural rent, ra,
and that given population density,
equals the agricultural rent, ra,
and that given population density, 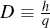 , the population fits
inside
, the population fits
inside 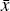 .
These are
.
These are
and
Given Equations (A1) to (A4), Equations (A5) and (A6) simultaneously determine the
equilibrium values of 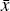 and u.
and u.
FAR restriction
A FAR restriction imposes an upper bound on the floor space of housing produced per
unit of land. Following Bertaud and Brueckner (2005), such restriction takes
the form, h(S) ≤ ĥ. Because h falls with
distance, the constraint will bind closer to the centre and will not bind further
out. If 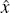 denotes the location where the FAR restriction becomes binding, then the equilibrium
conditions are given by
denotes the location where the FAR restriction becomes binding, then the equilibrium
conditions are given by
The system of Equations (A7)–(A9) determine the equilibrium values of 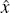 ,
,
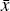 ,
and u.
,
and u.
Calibration and functional forms
Following Bertaud and Brueckner (2005), we assume for tractability Cobb-Douglas utility
and production functions of the form, 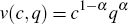 and
and 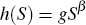 .
Table A1 below summarises the benchmark calibration. In 2007–2008, mean
household disposable income per week was $1,366 (Household Income and Income
Distribution, Australia, 2007–08, ABS Cat No 6523.0, Appendix 3, Table
A5.) This implies an annual income of $71,032, which we round to $70,000. Based
on 2005/06 data (Year Book Australia 2008, ABS Cat No 1301.0), average weekly
housing costs for all household types was $185, which implies an α
of about
0.14.[28]
We assume the city's population is 2 million, living in 800,000 households
of an average size of 2.5 persons per household.
.
Table A1 below summarises the benchmark calibration. In 2007–2008, mean
household disposable income per week was $1,366 (Household Income and Income
Distribution, Australia, 2007–08, ABS Cat No 6523.0, Appendix 3, Table
A5.) This implies an annual income of $71,032, which we round to $70,000. Based
on 2005/06 data (Year Book Australia 2008, ABS Cat No 1301.0), average weekly
housing costs for all household types was $185, which implies an α
of about
0.14.[28]
We assume the city's population is 2 million, living in 800,000 households
of an average size of 2.5 persons per household.
| Parameter | Description | Value |
|---|---|---|
| y | Income ($/year) | 70,000 |
| α | Utility function – expenditure share on housing | 0.14 |
| β | Housing production function parameter on structures | 0.60 |
| g | Scaling on the housing production function | 0.0005 |
| i | Price of capital | 1 |
| t | Transport costs ($/year/km) | 600 |
| θ | Radians available for construction | 3 |
| ra | Agricultural land rent ($/km2/year) | 45,000 |
| L | Population | 2,000,000 |
Agricultural land rent is a broad average of the rental prices of coastal grazing and wheat properties using New South Wales land data, assuming a 10 per cent rate of return (see <http://www.lpma.nsw.gov.au/valuation/nsw_land_values>).
To estimate transport costs, we follow Bertaud and Brueckner (2005) methodology. We assume 1.35 workers per households and 40 hours work per week so that the hourly wage is $25.30. Assuming the commute time is valued at 60 per cent of the wage rate, and traffic moves at 50km/hour the time cost of commuting is $0.30/km per worker. According to the NRMA, in 2008 the operating cost of a medium-sized car is about $0.67/km. Together, this means the transport cost is $0.97/km per worker. Grossing up by the number of workers per household (1.35) and the number of trips per year (240 work days per year), and then multiplying by two to account for return trips, total commuting cost is $628 per year. We round this to $600.
Footnotes
The analysis is of the absentee-owner version of the model, whereby households implicitly pay rent to landlords outside the city. See Pines and Sadka (1986) for a model where land is internally owned. [27]
The share of expenditure on housing is estimated to be somewhat higher in the 2009/10 Household Expenditure Survey, which became available after this paper was finalised. While different assumptions for this parameter, or for average household income, will result in slightly quantitative results, the broad economic relationships identified in the calibration exercise are all robust to changes in these parameters. [28]