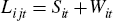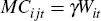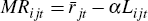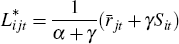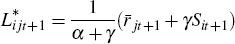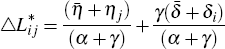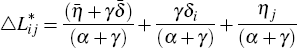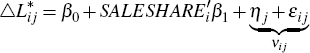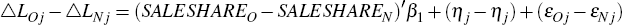RDP 2013-05: Liquidity Shocks and the US Housing Credit Crisis of 2007–2008 Appendix A: Identifying the Effect of Credit Supply Shocks
May 2013 – ISSN 1320-7229 (Print), ISSN 1448-5109 (Online)
- Download the Paper 756KB
In this Appendix I outline a model that describes how credit demand and supply shocks affect mortgage lending. The model is closely related to that of Khwaja and Mian (2008). The purpose of the model is to highlight the identification problem and explain the construction of the estimator that controls for credit demand shocks. In this simple model I assume that each bank i lends to region j at time t the amount Lijt. There are two time periods. I assume that each bank can lend to only one region, but a region can borrow from multiple banks. On the credit supply side, I assume that each bank loan to a particular region is financed through a combination of securitisation Sit and other forms of external financing Wit. These assumptions generate the following flow of funds constraint:
I assume that the bank can securitise loans at no cost, but, importantly, there is
a quantitative limit on how much the bank can securitise (i.e. Sit < 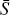 ). Beyond this limit, the bank must turn to
costly external finance to support higher levels of lending. These assumptions
ensure that the level of securitisation matters to the lending decision of
each bank. If there was no limit on securitisation and/or no cost of accessing
external finance, then the funding structure of the bank would not affect
lending.[15] Under
this set of assumptions, the marginal cost of lending for the bank is solely
a function of the volume of wholesale debt (i.e. external finance):
). Beyond this limit, the bank must turn to
costly external finance to support higher levels of lending. These assumptions
ensure that the level of securitisation matters to the lending decision of
each bank. If there was no limit on securitisation and/or no cost of accessing
external finance, then the funding structure of the bank would not affect
lending.[15] Under
this set of assumptions, the marginal cost of lending for the bank is solely
a function of the volume of wholesale debt (i.e. external finance):
The cost parameter (γ > 0) denotes the slope of the marginal cost curve. On the credit demand side, I assume the marginal loan return is given by the following equation:
The borrower quality parameter 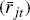 allows for variation in loan returns across regions. Given the slope parameter (α)
is a positive constant, the formulation assumes that there are diminishing
marginal returns to borrowing. I solve for the first-period equilibrium by
equating marginal revenue with marginal cost and substituting the flow of funds
identity:
allows for variation in loan returns across regions. Given the slope parameter (α)
is a positive constant, the formulation assumes that there are diminishing
marginal returns to borrowing. I solve for the first-period equilibrium by
equating marginal revenue with marginal cost and substituting the flow of funds
identity:
where the superscript ‘*’ denotes equilibrium. At the end of the first period, the credit market experiences two types of shocks:
-
Credit demand shock:
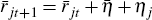
-
Credit supply shock:
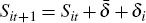 .
.
The credit demand shock consists of two terms – an aggregate shock that is
common to all regions 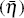 and an idiosyncratic shock that is specific to each region (ηj).
In terms of the econometric framework, the aggregate credit demand shock might
be an unexpected change in US monetary policy while the region-specific demand
shock might be a shock to regional house prices. The credit supply shock also
consists of two terms – an aggregate shock that is common to all banks
and an idiosyncratic shock that is specific to each region (ηj).
In terms of the econometric framework, the aggregate credit demand shock might
be an unexpected change in US monetary policy while the region-specific demand
shock might be a shock to regional house prices. The credit supply shock also
consists of two terms – an aggregate shock that is common to all banks
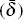 and a bank-specific shock (δi). The aggregate credit supply
shock might reflect some change in financial regulation that affects the ability
of banks to securitise loans while the bank-specific credit supply shock could
reflect each bank's ability to securitise assets.
and a bank-specific shock (δi). The aggregate credit supply
shock might reflect some change in financial regulation that affects the ability
of banks to securitise loans while the bank-specific credit supply shock could
reflect each bank's ability to securitise assets.
Following the same approach as before, I solve for the second-period equilibrium:
As the two solutions are linear, I can then take the difference in (equilibrium)
lending over time 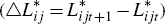 to obtain:
to obtain:
The change in the amount of each loan consists of two terms. The first term on the right-hand side denotes the impact of the region-specific credit demand shocks. The second term denotes the impact of the bank-specific supply shocks. If there is no cost of external finance (γ = 0), the credit supply shocks will not affect the equilibrium growth rate of lending; lending growth will only be a function of demand shocks. In other words, credit supply shocks only matter if there are financing frictions on the lender side.
Now suppose I re-arrange the equation to combine all the aggregate shocks in a single term and have two separate terms for the bank-specific and region-specific shocks:
If I assume that the share of loans that are securitised (SALESHAREi) by each bank is a suitable proxy for the bank-specific credit supply shock (δi) then I could run the OLS regression:
where there is an intercept that captures all the aggregate effects 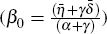 ,
a slope coefficient
,
a slope coefficient 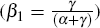 that captures the relationship of interest
and a composite error term (νij) which consists of a
region-specific component (ηj) and a bank-region specific
component (εij). If the share of loans that are
securitised (SALESHAREi) is correlated with the
unobservable credit demand shocks (ηj) then the OLS
estimate of β1 will be biased. But suppose the region
borrows from both an OTD lender and an non-OTD lender. Denote the OTD lender
with subscript O and the non-OTD lender with subscript N.
For a region j that has a loan from each type of bank, the within-region
difference in lending growth is:
that captures the relationship of interest
and a composite error term (νij) which consists of a
region-specific component (ηj) and a bank-region specific
component (εij). If the share of loans that are
securitised (SALESHAREi) is correlated with the
unobservable credit demand shocks (ηj) then the OLS
estimate of β1 will be biased. But suppose the region
borrows from both an OTD lender and an non-OTD lender. Denote the OTD lender
with subscript O and the non-OTD lender with subscript N.
For a region j that has a loan from each type of bank, the within-region
difference in lending growth is:
This equation eliminates both the effect of the aggregate shocks and the unobservable region-specific credit demand shocks. Equivalently, the OLS regression with the inclusion of borrower-specific fixed effects controls for the unobservable credit demand shocks (ηj). An unbiased estimate of the causal effect of the credit supply shock can be obtained under the identifying assumption that each bank's loan securitisation share is uncorrelated with the bank-region specific errors (corr(SALESHAREi,εij) = 0)).
Footnote
I further assume that the bank cannot fund loans through internal finance (e.g. retained
earnings or deposits). While this appears to be a strong assumption, it is
only made to simplify the algebra – the results still hold if I instead
assume that banks finance lending through deposits (Dit), where deposits are the cheapest form of funding.
In that case, the key assumptions are that there is also a quantitative limit
on internal finance (i.e. Dit < 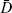 ) and that securitisation
is a cheaper form of funding than other forms of external finance.
[15]
) and that securitisation
is a cheaper form of funding than other forms of external finance.
[15]