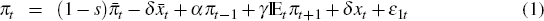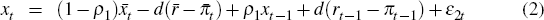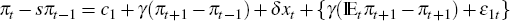RDP 2013-11: Issues in Estimating New-Keynesian Phillips Curves in the Presence of Unknown Structural Change 2. The Model and Estimators

We will be working with the simple three-equation system that is a basic construct of the NK framework. These equations are:

where π_t is inflation, x_t is the log of output (or real marginal cost) and r_t is the nominal interest rate. The parameter s = α + γ is the sum of the coefficients on π_t−1 and 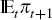in the Phillips curve. Over-bars mean equilibrium solutions.

The only two equilibrium values that are assumed to change are the inflation target, 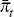, and the log of potential output, 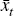. One can re-express the equations above in terms of the deviations of variables from their equilibrium values, which is how the NK system is generally presented. It is known that when 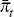and 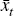vary one might expect the parameters of the NKPC, Equation (1), to be dependent on these quantities, and so be changing as well – see Ascari (2004) and Cogley and Sbordone (2008). Although our solution algorithm also allows for the parameters to be indexed by time, we want to focus on how changing equilibrium values affect the estimators of the NKPC coefficients, as that has been the focus in the literature.

We can think of two possible IV estimators of the Phillips curve in Equation (1). The first – called the restricted IV estimator (RE) – works with the reparameterised equation (where the term {γ( 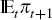− π_t+1) + ε_1t} is the error term):

As there are three coefficients to be estimated, c₁, γ and δ, we need at least three instruments. Variables that are uncorrelated with ε_1t provide instruments for the regressors and these are π_t−1, x_t, x_t−1 and r_t−1. x_t qualifies as an instrument because only lagged values determine it and ε_2t is uncorrelated with ε_1t. Appendix A shows that π_t+1 depends on x_t, π_t−1 and r_t−1 but not x_t−1. Hence x_t−1 is not a relevant instrument for π_t+1, a fact noted by Pesaran (1987), when d in Equation (2) is zero.

For the second IV estimator, called the unrestricted estimator (UE), the model estimated is:

in this case, π_t−1, x_t and r_t−1 provide exactly the right number of instruments for the three variables π_t−1, π_t+1 and x_t. In much empirical work, a broader set of instruments is assumed without specifying a model, but it is useful to have a small model from which to generate the instruments.