RDP 2013-14: Reserves of Natural Resources in a Small Open Economy 4. Natural Resources in a Small Open Economy
December 2013 – ISSN 1320-7229 (Print), ISSN 1448-5109 (Online)
- Download the Paper 863KB
In general equilibrium, we assume that the resource sector is largely identical to that previously discussed:
However, to properly integrate a resource firms' problem within general equilibrium we require two further assumptions. The first assumption is that we now explicitly account for the preferences of resource firm owners. This is done by assuming that firms use a stochastic discount factor (SDF), βMt,t+1, when valuing profits over time and states of the world, rather than the deterministic discount factor, β. For simplicity, and consistent with the presence of foreign ownership in the sector, we assume that the SDF for resource firms only partially updates to reflect the preferences of the domestic owners and is thus given by:
where ν is the parameter governing the importance of domestic ownership and Θt is the marginal utility of (domestic household) consumption in period t.
The second assumption is that exploration activity requires non-traded goods as an input:[18]
where  is aggregated using a using the Dixit-Stiglitz aggregator:
is aggregated using a using the Dixit-Stiglitz aggregator:
We now briefly describe the rest of the small open economy (a more complete discussion is available in Appendix D). Concerning production in the rest of the economy, we assume that there are three sectors: a non-traded sector; an importing sector; and a non-resource exporting sector. All three sectors are assumed to operate in a monopolistically competitive environment and face a Calvo price-setting friction. Prices in all sectors are set in local (domestic) currency terms and these sectors are owned by domestic households.
Non-traded firms produce an intermediate input, which when bundled with the production of their competitors, is either consumed, used as an input in non-resource export production, or used as an input in the resource exploration process. Importers import a final good from abroad and then differentiate it to produce a specialised good that is consumed by domestic residents. Non-resource exporters transform a bundle of non-traded intermediate goods into a specialised good that is exported abroad.
For domestic (household) demand, we assume that domestic households have consumption habits in the spirit of ‘keeping up with the Jones’ (Abel 1990). We include this mechanism to allow for a non-unitary intertemporal elasticity of substitution (IES), which is important for matching the empirical data, while keeping the model tractable when finding its stationary representation.[19] We further assume that households view work in the resource and non-resource sectors as imperfect substitutes, which is captured through a constant elasticity of substitution (CES) function.
Although we assume complete insurance among identical individual households, allowing for the modelling device of a representative household, we assume that international financial markets are incomplete in the spirit of Benigno and Thoenissen (2008). Specifically, households can trade in either a domestic bond or a foreign bond, where the latter is subject to an endogenous risk premium.[20] This premium is governed by both the domestic economy's capacity to repay foreign debt (measured as the stock of foreign assets in domestic currency terms scaled by the stock of domestic reserves) and the relative valuation differential between the the real exchange rate and resource prices.
We include the relative valuation differential to capture the idea that changes in the real exchange rate and resource prices can have direct effects on risk premia. For example, higher resource prices and an appreciated real exchange could affect the ability to repay foreign liabilities, even with the value of these foreign liabilities (in domestic currency terms) remaining unchanged. The size of this effect is estimated and is important when matching the dynamics of the real exchange rate in response to a resource price shock (see Table 3 and Figure 5).
Our estimates suggest that a 1 per cent increase in real resource prices (or a 1 per cent appreciation in the real exchange rate) reduces the foreign risk premium by about 25 basis points after one year. This is consistent with higher resource prices increasing domestic wealth, and so the capacity to repay existing and new debt obligations. A real appreciation of the same magnitude could also imply greater capacity to repay as an appreciated real exchange rate implies that a unit of domestic goods is now worth more in foreign currency terms and could, at least in principle, be pledged as greater collateral when borrowing from abroad.
For the rest of the world – defined as the foreign price level (in foreign currency terms), non-resource demand, foreign interest rates, and the price of imported resource-specific capital (again in foreign currency terms) – we assume a reduced-form VAR.[21] This is a simplification allowing us to focus on the effects of a resource price shock, holding all other international prices and quantities constant. Although we acknowledge that the source of foreign structural shocks can be important, we view this as an extension of our work given that our first-order interest is in studying the mechanism of interest, endogenous reserves, in a transparent way.[22]
We assume resource prices follow an AR(1) process, consistent with previous literature that assumes exogenous reserves. All markets clear in our economy and we assume that domestic monetary policy follows a simple Taylor rule, allowing for both interest-rate smoothing and a response to expected domestic inflation.
Overall, our approach is quite similar to existing small open economy (SOE) models such as that described in Adolfson et al (2007) and Jääskelä and Nimark (2008). We use a minimal level of structure to ensure that our economy is able to reproduce some basic empirical regularities such as the existence of non-tradeable production, non-resource export activity, incomplete pass-through, and a time-varying link between the marginal utility of domestic consumption and the real exchange rate. This minimal level of structure retains tractability and allows us to focus on the mechanism of interest, endogenous reserves.
4.1 Calibration
Most parameters in our general equilibrium model are calibrated. We use the same calibration for the resource sector parameters presented in the upper panel of Table 1. For the rest of the domestic economy, our calibrated parameters are chosen to be in line with the results in Jääskelä and Nimark (2008). These authors estimate a model with a relatively similar production structure to ours and Adolfson et al (2007) using Australian data, but with a simple reduced-form for the resource (commodity) sector.[23]
The parameters we choose are adjusted to match an annual time horizon and are summarised in Table 2. We assume identical elasticities of substitution within the non-traded goods, importing and non-resource export sectors, each consistent with a mark-up of approximately 17 per cent. We further assume identical price stickiness parameters, each implying a 20 per cent probability that a firm cannot re-optimise its price within a year's time.
| Description | Coefficient | Value |
|---|---|---|
| Household discount factor | β | 0.96 |
| Labour convexity | ξh | 4 |
| Labour substitution parameter | γh | 0.5 |
| Consumption substitution elasticity | ηc | 1.01 |
| Home-bias coefficient | 1−α | 0.8 |
| Substitution elasticity (within non-traded goods) | θn | 7 |
| Substitution elasticity (within imports) | θo | 7 |
| Substitution elasticity (within non-resource exports) | θx | 7 |
| Substitution elasticity (across non-resource exports) | θ* | 1 |
| Calvo parameter (non-traded goods) | ϕn | 0.2 |
| Calvo parameter (imports) | ϕo | 0.2 |
| Calvo parameter (non-resource exports) | ϕx | 0.2 |
We choose the home bias parameter to match a 20 per cent import share in steady state, and an elasticity of substitution between consumption of non-traded goods and imports that is close to one (Cobb-Douglas consumption preferences). We set the elasticity of substitution between resource and non-resource labour supply at 1, and fix the overall convexity parameter of labour disutility at 4. These assumptions imply that labour is relatively substitutable between sectors, but that households are averse to increasing their overall supply of labour to the economy.
4.2 Estimation
The remaining parameters of the model are estimated using a GMM procedure that matches the IRFs of the empirical VAR, discussed in Section 2, and the IRFs of our theoretical model in general equilibrium with endogenous reserves. Specifically, we minimise the following measure of distance
where θ is a vector of the parameters to be estimated, j
relates to the observable variable being matched (either resource prices, the
real exchange rate, inflation, the ratio of non-mining GDP to reserves, or
the ratio of mining capital expenditure to reserves), l denotes the
time horizon from the initial impulse (one being the period in which the resource
price shock occurs),  (θ) is the IRF implied by
our theoretical model evaluated at θ,
(θ) is the IRF implied by
our theoretical model evaluated at θ,  is the estimated IRF
from the VAR, and Wjl is a diagonal matrix that weights
the deviations between the theoretical model and the VAR IRFs by the width
of the 95 per cent confidence interval at each IRF point (as estimated using
the VAR).
is the estimated IRF
from the VAR, and Wjl is a diagonal matrix that weights
the deviations between the theoretical model and the VAR IRFs by the width
of the 95 per cent confidence interval at each IRF point (as estimated using
the VAR).
The results of this estimation procedure are reported in Table 3 and the fit of the best matching model is reported in Figure 2. The importance of domestic ownership for resource firms' stochastic discount factor is estimated at 0.35, which is similar to estimates of domestic ownership in the resource sector (see, for example, Connolly and Orsmond (2011)). The estimated coefficient of relative risk aversion is high at 10, although it is in line with the values required to rationalise the equity premium puzzle (see, for example, Mehra and Prescott (1985) and Constantinides (1990)).[24]
| Description | Coefficient | Value |
|---|---|---|
| Risk aversion coefficient | ξc | 10 |
| Domestic ownership parameter | ν | 0.35 |
| Risk premium (repayment capacity) | φb | 200 |
| Risk premium (valuation dynamics) | φs | 0.25 |
| Exploration costs dynamics | ϕmc | 0.5 |
| Investment cost parameter | κ | 3 |
| Responsiveness parameter (marginal costs) | ϒ | 0.33 |
| AR(1) parameter (prices) | ρx | 0.9 |
| Interest rate smoothing paramerter | ρi | 0.2 |
| Taylor rule parameter (inflation) | ρπ | 5 |
The elasticity of the foreign risk premium with respect to debt scaled by domestic reserves appears large but this represents the effect of scaling. When considered on the metric of the induced percentage point movement in the foreign risk premium, this parameter appears plausible (see Figure 5). Consistent with the IRFs obtained from the VAR, resource prices are estimated to follow a very persistent process with an autoregressive parameter of 0.9.
Interestingly, the data favour a model where non-traded firms' marginal costs respond directly to changes in resource prices, ϒ=0.33, and so there appears to be some input-cost inflation reflecting the correlation between energy and resource prices (for further discussion, see Appendix D). Estimates for the parameters regarding investment adjustment costs and exploration costs appear plausible, with the latter suggesting exploration costs increase at a faster rate than discovered reserves.
4.3 Results
Figure 4 shows the response of the resource sector to a 1 per cent increase in resource prices in general equilibrium and compares the models with exogenous reserves and endogenous reserves.[25] The first point to note is that the amplification effects associated with the inclusion of endogenous reserves remain in general equilibrium. A persistent increase in resource prices prompts firm to increase both exploration and extraction, as the marginal returns to production and the value of new reserves remain high for a period. When exploration results in the discovery of new reserves, this gives firms an additional incentive to extract more now and in future periods – leading to greater demand for labour and capital – as marginal production costs fall.
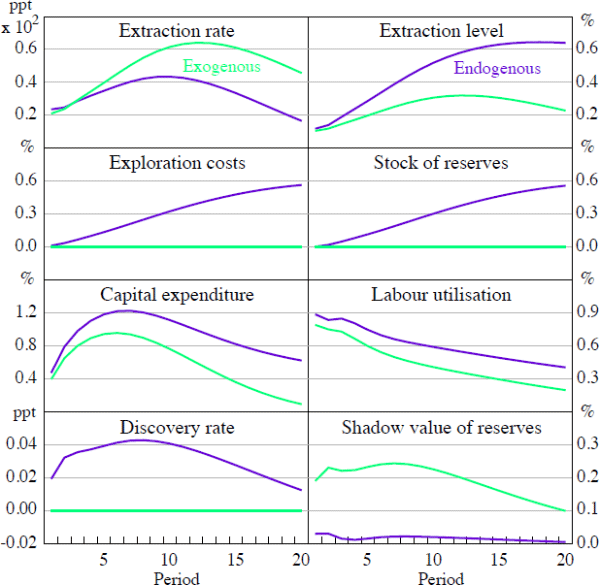
Nevertheless, it is also clear that the degree of amplification attributable to endogenous reserves is smaller than in the partial equilibrium case. This occurs because the appreciation of the real exchange rate offsets part of the increase in the value of resource export receipts. Also, greater demand for labour induces an increase in wages paid in the sector and the prices of non-traded inputs rise in general equilibrium. These effects increase the costs of expansion in the resource sector, both in terms of production and exploration, and so the divergence between the IRFs in the endogenous and exogenous models, while still economically significant, are smaller than indicated by the previous partial equilibrium results.
The amplification effects of a resource price shock are also present in domestic activity (Figure 5). Comparing the responses with endogenous and exogenous reserves respectively, one can see that the declines in consumption (both aggregate and imported) and non-resource exports, relative to the steady state baseline, are larger with endogenous reserves. This is because the expansion in the resource sector absorbs a greater fraction of domestic intermediate inputs, and is consistent with the rise in expected real interest rates required to stabilise inflation. In terms of the effect on total domestic production, we find that this is close to zero because the declines in consumption and non-resource export demand are almost fully offset by the expansion of demand from the resource sector. Thus, although sectoral reallocation (the Dutch Disease) is amplified under endogenous reserves, it does not have significant implications for domestic production overall.
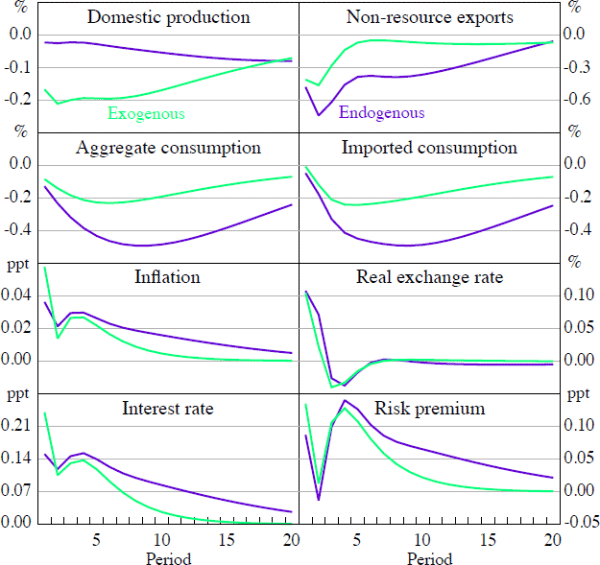
With exogenous reserves, there is no longer an additional income or aggregate demand effect associated with the discovery of new reserves. This is reflected in a smaller expansion of the resource sector, and a noticeable decline in domestic production in response to a resource price shock. In this case, although there are smaller falls in consumption and non-resource export demand (that is, less Dutch Disease effects), the smaller expansion of the resource sector is not sufficient to offset the declines in demand from these other areas of activity. In sum, there is less sectoral reallocation of goods, but also less domestic production overall.
For domestic inflation, the domestic interest rate, and the foreign risk premium, the inclusion of endogenous reserves increases the time it takes for prices to converge back to their steady state path (i.e. the persistence of the IRFs), but does not amplify their effect when the shock first arrives (Figure 5). If anything the contemporaneous effects on these prices appear smaller when reserves are endogenous. For the real exchange rate, the propagation of the shock is largely unaltered with an initial appreciation of the real exchange rate followed by a small subsequent depreciation.[26]
Footnotes
Specifically, we are assuming that exploration expenditure and a bundle of non-traded goods are perfect complements required for the discovery of new reserves. [18]
Note that alternatives, such as constant relative risk aversion without a habit, substantially complicate detrending of the model even though they too allow for a non-unitary IES. [19]
We assume that the domestic bond is in zero net supply in equilibrium. [20]
The only restriction that we impose on this foreign VAR is that foreign demand for non-resource exports is cointegrated with the domestic stock of reserves. This is a technical device used to ensure that a stationary representation of our economy can be found. For further discussion on this point, see Appendix D.7. [21]
Although foreign structure is interesting, it would substantially complicate interpretation of the mechanism given that all foreign prices and quantities would move simultaneously when resource prices change. [22]
The main exception is for the calibration of the elasticity of substitution on imported goods. The estimate implied in Jääskelä and Nimark (2008) implies a very large mark-up on imported goods. We abstract from concern over whether this parameter is well identified and simply fix the implied mark-ups on domestically produced and imported goods to be identical. [23]
In the current context, a high relative risk aversion coefficient is required to limit the sensitivity of consumption to a resource price shock. All else constant, a lower value for this coefficient implies that consumption becomes too volatile. [24]
It should be clear that the IRFs measure changes relative to the baseline of a steady state or balanced growth path. [25]
The responses for the real exchange rate are inverted so that an appreciation in the figure is a movement upwards. [26]












