RDP 2014-07: International Trade Costs, Global Supply Chains and Value-added Trade in Australia Appendix A: Construction of Value-added Trade Estimates

This appendix outlines the input-output tables available in the WIOD and describes the construction of the key indicator of value-added trade – the VAX ratio. A multiregional input-output table (Figure A1) extends the traditional concept of an input-output table by concatenating matrices of inter-industry input use and vectors of final demand to record internal and cross-border flows of final and intermediate goods and services. The flows represent values rather than volumes. This implies a common set of prices and ensures the market clearing condition that overall revenue equals expenditure.

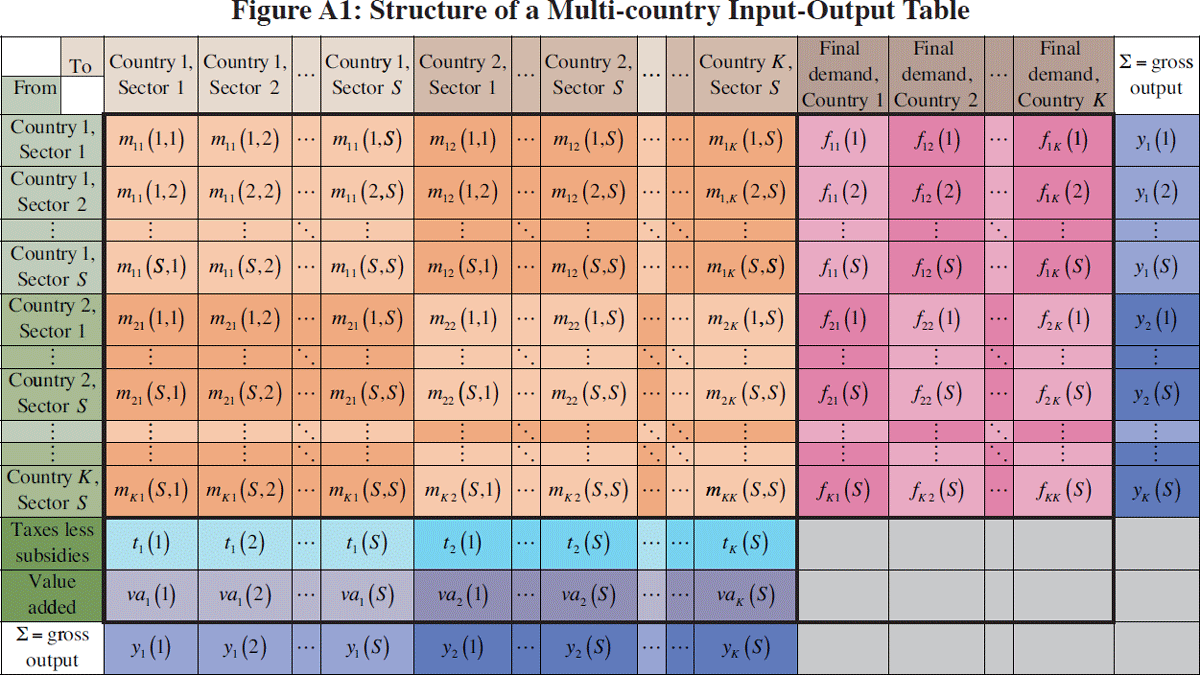
The columns of the table represent the inputs used by each industry in each country, with the total value of production equal to the sum of domestic inputs, imported inputs, taxes, margins, and value-added (the contribution of labour and capital). The rows of the table represent the output of each industry in each country, with total output equal to the sum of domestic intermediate use, domestic final use and exports.

Formally, the table entry m_ij(s, s′) denotes intermediate use of the output of sector s of country i by sector s′ in country j, while the entry f_ij (s) denotes final use of the output of sector s of country i by country j. Total output of sector s in country i is denoted , with y_i denoting the S × 1 vector of output for country i's S sectors and f_ij denoting the S × 1 vector of country j's final demand for the output of country i's S sectors.

Total exports of sector s in country i can be denoted x_i(s) = Σ_j≠i f_ij(s) + Σ_j≠iΣ_s′m_ij(s, s′).

The world input-output table contains information on the approximate technical requirements of production, which means that the value of intermediate inputs used in the k-th step of the production process can be derived from the values of final demand, i.e. those inputs that are used as direct inputs into final demand (first step), those that are used as inputs into those inputs (second step), and so on.

For a table of S sectors in N countries, taking y = (y₁, y₂,…, y_N)′ to be the SN × 1 vector of total world production, we can write y = Ay + f, where is the SN × 1 vector of total world final demand, and A is the technical requirements matrix, an SN × SN matrix with A_ij(s,s′) = m_ij(s,s′)/y_j(s′). Then A^k f gives the value of intermediate inputs used in the k-th step of the production process.

The succession of production stages continues indefinitely due to the ‘circular flow’ of the production process, with the sum of final and intermediate goods and services production converging to the full value of total gross output as the number of stages increases.

A circular production process involving an effectively infinite number of stages, with identical input requirements and output uses at each stage, is a basic assumption of input-output analysis. The infinite sum of successive powers of the technical requirements matrix A converges to . The matrix (I − A)⁻¹ is the ‘Leontief inverse’, which transforms the final demand vector into the gross output vector, i.e. y = (I − A)⁻¹f, which is simply a rearrangement of y = Ay + f.

By decomposing the final demand vector by region, we can estimate the total value of domestic production that is attributable to final demand in various parts of the world.

Similarly the S × 1 vector of output from country i used to produce goods in country j (denoted y_ij) is derived as .

The ratio r_i(s) of value-added to gross output in sector s of country i is defined as one minus the intermediate consumption share of output; r_i(s) = 1 − Σ_jΣ_s′A_ji(s′, s).^[26] Total value-added exports from country i are then given by va_i = Σ_j≠iΣ_sva_ij(s) where va_ij(s) = r_i(s)y_ij(s). This implicitly assumes that the share of value-added to gross output is the same for all products of an industry, regardless of whether the products are exported or not.

The ratio of bilateral value-added to gross exports from sector s of country i to country j is then VAX_ij(s) = va_ijj(s)/x_ij(s).

Footnote

More precisely, value-added also excludes the value of taxes less subsidies. [26]